공학 문제를 풀다보면 흔하게 등장하는 근사는
$\sin x \approx x \quad \text{if }x \ll 1$이다.
이 가정이 통하는 구간이 대략 어느정도인지 알아보았다.
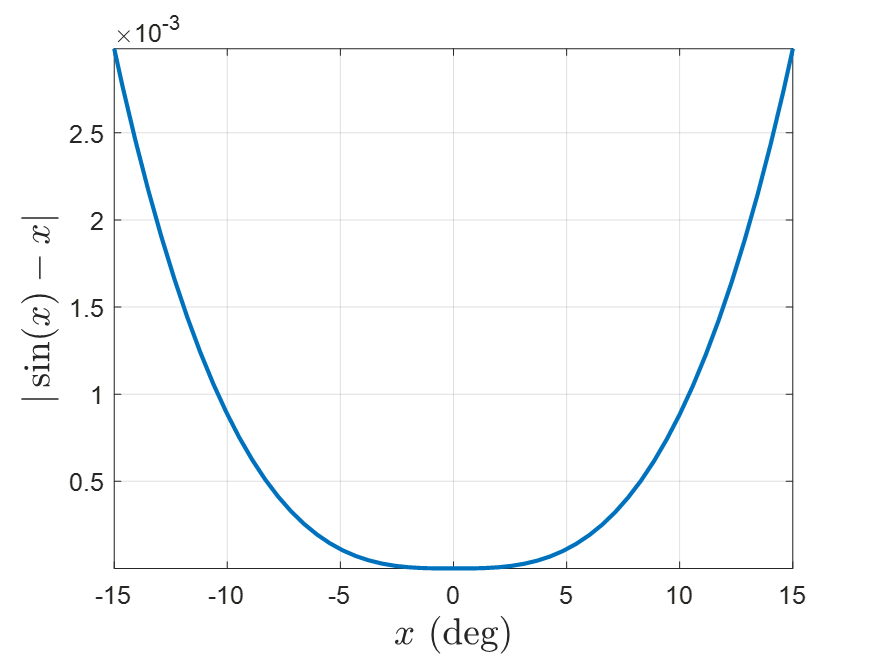
15도 정도여도 충분히 그럴 듯한 가정이다. 고작 $2e-03$ 정도밖에 차이나지 않는다.
마찬가지로 $\cos x \approx 1 $ 역시 자주 쓰이는 가정인데
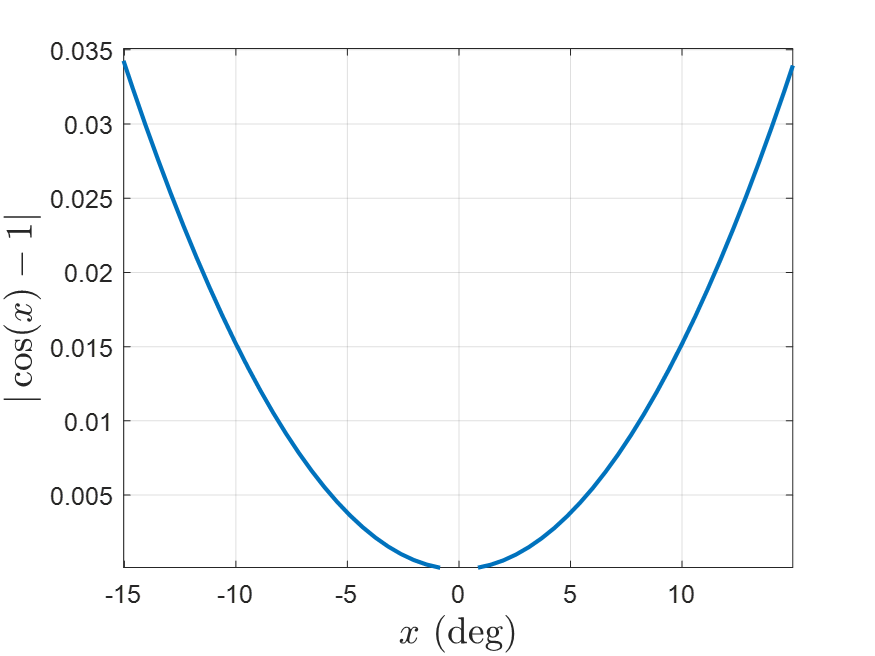
이 경우에는 거의 5도에 근접해야 차이가 거의 나지 않는다.
아래는 작성한 코드.
x = -1/4*pi: 0.01 : 1/4*pi ;
R2D = 180/pi ;
figure ;
plot(x * R2D, abs( sin(x) - x ), 'linewidth', 2.0) ;
xlabel('$x$ (deg)') ;
ylabel('$|\sin(x)-x|$') ;
figure ;
plot(x * R2D, abs( cos(x) - 1 ), 'linewidth', 2.0) ;
xlabel('$x$ (deg)') ;
ylabel('$|\cos(x)-1|$') ;'기타' 카테고리의 다른 글
| [기록] C드라이브 포맷 후 D드라이브에 있는 프로그램 인식 안됨 (0) | 2022.12.23 |
|---|---|
| [기타] 대학원생에게 유용한 프로그램 정리 (1) 수식 관련 (0) | 2022.12.12 |
| [기타] 왜 단축키가 안 먹힐까? 왜 수식 폰트가 다르게 나올까? - 한글 변환기 제거 (0) | 2022.08.14 |
| [기타] 색상 RGB, HEX 코드 알아내는 방법 (0) | 2022.07.17 |
| 노이즈(noise) 종류 (0) | 2021.09.27 |