output에 대한 input의 gradient를 구하는 방법은 여러가지인데
input tensor에 대해 requires_grad는 반드시 True로 지정해야 한다. 그래야 gradient 추적이 가능하다.
그 다음에는 두 가지 방법으로 나뉜다.
1. backward()를 이용하고 (input tensor).grad를 통해 가져오는 방법
2. torch.autograd.grad를 이용해서 직접 계산하는 방법
1번이 전형적으로 gradient를 구하는 방법이지만 나는 얻어낸 gradient에 대하여 graph를 연장해야했다. 그러려면 1번 방법으로는 충분하지 않다.
그래서 2번을 해야하는데 multioutput일 때는 gradient에 대한 이해도가 좀 더 요구되는 편이다.
1번 방법. backward() 사용하기
pred = dnn(input_x) # (batch size, output num)
num = input_x.shape[0] # batch size
for i in range(6):
pred[:,i].backward(torch.ones((num)), retain_graph = True) # gradient 계산
temp_grad = input_x.grad[:,0] # 첫번째 input에 대한 gradient
input_x.grad = None
self.dnn.zero_grad()
이 경우에는 직접적으로 output의 feature 중 하나를 지정해서 이에 대해 backward를 하고 input의 여러 개의 feature 중에서 하나를 골라서 이 gradient를 temp_grad에 저장하는 코드이다.
여러 개의 output이 있을 때 훨씬 직관적으로 각 output마다의 input에 대한 gradient를 구할 수 있다.
주의할 점은 backward는 모든 변수에 대한 gradient를 구하기 때문에 model의 gradient를 모두 초기화해줘야 중복없이 구할 수 있다는 점이다.
2번 방법. autograd.grad를 사용하는 방법
autograd.grad는 pytorch에서 굳이 모든 변수(weight, bias 등)에 대해 gradient를 구하지 않더라도 개별적으로 원하는 input과 output에 대하여 gradient를 구하도록 만들어준 함수이다.
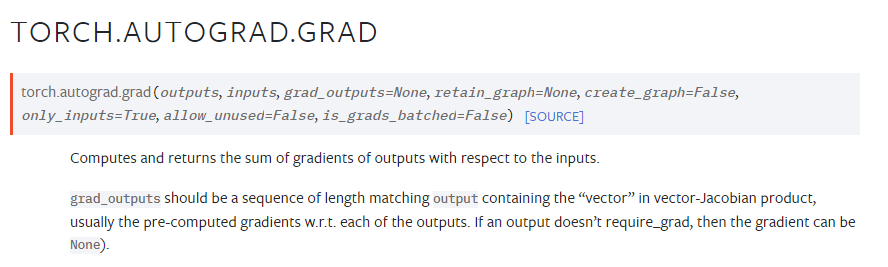
그런데 설명을 보면 grad_outputs should be a sequence of length matching output containing the "vector" in vector-Jacobian product, usally the pre-computed gradients w.r.t each of the outputs.라고 적혀있다.
output와 일치하는 길이여야한다는 뜻이다. 사실 정확히 뭘 의도하고 썼는지는 모르겠다..
다만 input의 feature가 5개이고, output이 1개인 경우에 gradient는 5개 원소를 가진 vector가 된다. 그런데 보통은 input이 feature 5개를 가진 여러 개의 데이터이므로 (batch size * feature) 형태가 된다.
그러면 gradient는 (batch size * 5)처럼 될 것이다.
output은 (batch size * 1)이 된다. 이럴 경우 grad_outputs는 batch size만큼의 1로 구성된 벡터를 넣어줘야 제대로 된 결과가 나온다.
One Input - One Output인 경우
(feature 기준으로 one input이라는 뜻이지, batch size가 1이라는 뜻이 아니다)
a = torch.autograd.grad(pred, input_x, torch.ones(input_x.shape[0]), retain_graph=True, create_graph=True)[0]
여기에서 첫 번째 argument가 output (batch size * 1)이고, 두 번째 argument가 input (batch size * 1)
세 번째 argument는 사이즈가 (batch_size * 1)이자 모든 원소가 1로 된 벡터이다.
output을 input에 대한 derivative를 구하면 (batch_size * 1)이 되기 때문에 grad_output으로 사용한다.
참고로 저 코드의 맨 끝에 [0]을 하는 이유는 torch.autograd.grad가 tuple을 return하기 때문인데 특정 조건에서는 여러 원소를 가진 tuple을 내뱉는다.
Multi input One output인 경우
input의 feature가 n개일 때 input size는 (batch size, n)이 된다. 그러면
a = torch.autograd.grad(pred, input_x, torch.ones((input_x.shape[0],1)), retain_graph=True, create_graph=True)[0]위의 코드를 그대로 실행할 경우에 gradient를 구한 a는 (batch size, n)이 되어야한다.
grad_outputs 자리에 그대로 torch.ones(input_x.shape[0])를 써도 되는 이유는 grad_outputs 자리는 output 사이즈와 일치하도록 되어있기 때문이다.
multivariate scalar function의 경우 gradient를 구하면 벡터가 된다는 점을 기억하자. 그게 batch size만큼 있어야하므로 행렬이 된다.
Multi Input Multi Output인 경우
위에서 사용한 것처럼 쓰고 싶지만 이 경우에는 좀 더 고민해야한다.
Input의 feature가 n개이고 Output의 feature가 m개인 경우를 보자. 그러면 총 gradient는 (batch size * n * m)일 것이다.
multivariate vector function을 생각해보면 gradient는 m*n 또는 n*m으로 나타난다.
그런데 앞서 grad_outputs는 output의 사이즈와 동일하게 설정해야 한다고 했다. 즉, 세 번째 argument(grad_outputs)는 무조건 (batch size * m)으로 구성된다. (앞에서는 m=1인 경우였다.)
다음 예시를 보자.
layers = np.array([2,10,3])
model = NeuralNetwork(layers).to(device) # neural networks
x_temp = np.random.rand(10,2) # batch size = 10
x_temp = torch.tensor(x_temp)
x_temp.requires_grad_(True)
pred = model(x_temp)
temp_matrix = torch.ones((10,3))
a = torch.autograd.grad(pred, x_temp, temp_matrix, retain_graph=True)[0]
print(a.shape)
print(a)다음과 같은 경우에 grad_outputs는 전체가 1로 구성된 matrix를 집어넣었다.
결과는 다음과 같다.
torch.Size([10, 2])
tensor([[ 0.6447, -0.1288],
[ 0.6449, -0.1034],
[ 0.6863, -0.1955],
[ 0.6803, -0.1834],
[ 0.6586, -0.1208],
[ 0.6912, -0.2072],
[ 0.6558, -0.1158],
[ 0.6510, -0.1970],
[ 0.6641, -0.1711],
[ 0.6712, -0.2041]])
gradient가 (batch size * n)로 나왔다. 그런데 내가 원하는 것은 (batch size * n * m) 이라는 3차원 텐서였다.
저 값은 무슨 의미일까?
다음 코드를 통해 그래디언트를 구해보자.
for i in range(3):
temp_matrix = torch.zeros((10,3))
temp_matrix[:,i] = 1
a = torch.autograd.grad(pred, x_temp, temp_matrix, retain_graph=True)[0]
print(a)이러면
각각
$M_1 = \begin{bmatrix}
1 & 0 & 0 \\
\vdots &\vdots &\vdots \\
1 & 0 & 0 \\
\end{bmatrix}, M_2 =\begin{bmatrix}
0 & 1 & 0 \\
\vdots & \vdots &\vdots \\
0 & 1 & 0 \\
\end{bmatrix}, M_3 =\begin{bmatrix}
0 & 0 & 1 \\
\vdots & \vdots&\vdots \\
0 & 0 & 1 \\
\end{bmatrix}$
인 matrix를 세 번째 argument로 써서 그래디언트를 구한다.
각각
tensor([[0.1839, 0.3528],
[0.2662, 0.3857],
[0.3235, 0.3912],
[0.2228, 0.3787],
[0.1425, 0.3658],
[0.2553, 0.3876],
[0.2445, 0.3873],
[0.2265, 0.3522],
[0.3263, 0.3924],
[0.3288, 0.3888]])
tensor([[-0.1607, -0.1637],
[-0.1323, -0.1101],
[-0.0955, -0.1123],
[-0.1443, -0.1437],
[-0.1766, -0.1379],
[-0.1360, -0.1143],
[-0.1349, -0.1341],
[-0.1384, -0.1670],
[-0.0894, -0.1175],
[-0.0949, -0.1082]])
tensor([[ 0.1362, -0.5564],
[ 0.3116, -0.3763],
[ 0.2860, -0.5034],
[ 0.2094, -0.5603],
[ 0.2305, -0.4038],
[ 0.3025, -0.4041],
[ 0.2408, -0.5479],
[ 0.1076, -0.6601],
[ 0.2644, -0.5746],
[ 0.2974, -0.4610]])으로 나온다. 가장 첫 번째 원소만 주목해서 보자. 그러면
0.1839 -0.1607+0.1362 = 0.1594
즉, 각 그래디언트의 첫 번째 원소를 더한 것이 위에서 본 0.1594와 일치함을 알 수 있다.
이 말은 무엇이냐면, 앞에서 본
$M =\begin{bmatrix}
1 & 1 & 1 \\
\vdots & \vdots&\vdots \\
1 & 1 & 1 \\
\end{bmatrix}$으로 세 번째 argument를 쓴 것은 각 output의 gradient를 구한 다음에 합한 것과 동일하다는 뜻이다.
마치 원래 그래디언트에서 batch size를 제외하고 (n*m) * (m)을 곱해준 것과 동일하게 된 꼴이다.
(1,1,1) 벡터를 곱하면 모든 output에 대한 그래디언트가 내적곱처럼 더해지는 것이다.
정확히 내부에서 어떤 연산이 일어나는지는 소스코드를 확인해봐야할 문제이지만,
개별 output에 대해 구하고 싶다면 바로 위 코드를 사용하는 것이 맞다.
좀 더 알게 되는 내용이 있으면 추가할 예정.
참고문헌
https://pytorch.org/docs/stable/generated/torch.autograd.grad.html
'프로그래밍 Programming > 파이썬 Python' 카테고리의 다른 글
| [Matplotlib] Matplotlib 폰트 스타일 바꾸기 (0) | 2023.01.13 |
|---|---|
| [PyTorch] 특정 조건에 맞는 텐서 출력/인덱싱 등 (2) | 2023.01.08 |
| [에러기록] matplotlib에서 figure만 그려지고 plot이 없는 경우 (0) | 2022.12.27 |
| [에러기록] Visual studio code에서 아나콘다 가상환경이 안 돌아갈 때 (0) | 2022.11.01 |
| [Matplotlib] Matplotlib savefig 기능 정리 (0) | 2022.08.21 |