Sampyl이라는 라이브러리를 사용하기 전에 간단한 예제가 있어서 posterior distribution과 sampler에 대한 tutorial을 좀 정리해보았다.
$\begin{aligned} & Y \sim N\left(\mu, \sigma^2\right) \\ & \mu=\beta_0+\beta_1 x_1+\beta_2 x_2\end{aligned}$
다음과 같이 $\beta$가 계수의 어떤 y와 x 간의 모델이 있다고 해보자. 이 문제에서는 $\beta=[2,1,4]$인 경우이다.
따라서 아래와 같이 $x_{0}=1, x_{1},x_{2}$에 대하여 $y$가 분포되어있다.
# Number of data points
N = 200
# True parameters
sigma = 1
true_b = np.array([2, 1, 4])
# Features, including a constant
X = np.ones((N, len(true_b)))
X[:,1:] = np.random.rand(N, len(true_b)-1)
# Outcomes
y = np.dot(X, true_b) + np.random.randn(N)*sigma
# visualization
plt.figure(figsize=(10.0, 4.8))
plt.subplot(1,3,1)
plt.scatter(X[:,0], y)
plt.xlim([-0.5, 2.5])
plt.ylabel('$y$')
plt.xlabel(r'$x_{0}$')
plt.subplot(1,3,2)
plt.scatter(X[:,1], y)
plt.xlim([-0.5, 1.5])
plt.xlabel(r'$x_{1}$')
plt.subplot(1,3,3)
plt.scatter(X[:,2], y)
plt.tight_layout()
plt.xlim([-0.5, 1.5])
plt.xlabel(r'$x_{2}$')
plt.show()
우리가 y라는 데이터를 $\sigma$만큼의 노이즈가 더해져서 관찰했을 때 적절한 $\beta$와 $\sigma$를 찾고 싶을 수 있다.
그래서 bayesian적인 접근을 사용해볼 수 있다. dataset인 $D$, 여기선 y값이 주어졌을 때 적절한 $\beta,\sigma$를 찾는 것이다. 이 '적절한'이라는 말은 모호한 말이다.
그래서 여기에서는 데이터가 주어질 때 $\beta,\sigma$가 나타날 확률 분포를 구하고 그 중에서 가장 높은 확률을 갖는 $\beta,\sigma$를 선정함으로써 모델을 식별할 수 있다. 이를 Maximum a posteri (MAP)라고 한다.
이 Posterior distribution을 구하기 위해서는 각 변수에 대한 확률 분포를 가정해야한다.
$\begin{aligned} P(\beta, \sigma \mid D) & \propto P(D \mid \beta, \sigma) P(\beta) P(\sigma) \\ P(D \mid \beta, \sigma) & \sim \operatorname{Normal}\left(\mu, \sigma^2\right) \\ \mu & =\sum \beta_i x_i \\ \beta & \sim \operatorname{Normal}(0,100) \\ \sigma & \sim \operatorname{Exponential}(1)\end{aligned}$
다음을 보면 우리가 구하고 싶은 $ P(\beta, \sigma \mid D)$는 $P(D \mid \beta, \sigma) P(\beta) P(\sigma) $이 세 개의 확률 분포의 곱과 비례함을 알 수 있다.
그렇다면 개별 확률 분포는 어떻게 구할까? 이는 사실 정답이 없다. 따라서 예제에서는 $\beta$를 normal distribution으로, $\sigma$를 exponential 로 가정하였다. 또한 우리가 처음에 y라는 measurement를 구했을 때의 모델처럼 $\mu=\beta_0+\beta_1 x_1+\beta_2 x_2$가 평균값이고, $\sigma$만큼의 표준편차를 가진 노이즈가 첨가된 것으로 가정하였다. 이는 사실 우리가 임의로 선정한 모델이라는 점을 기억하자. (비록 우리가 정말 저 모델을 써서 데이터를 생성했지만 이는 특수한 경우다. 보통은 모델 자체가 틀렸을 수도 있다.)
import sampyl as smp
from sampyl import np
# Here, b is a length 3 array of coefficients
def logp(b, sig):
model = smp.Model()
# Predicted value
y_hat = np.dot(X, b)
# Log-likelihood
model.add(smp.normal(y, mu=y_hat, sig=sig))
# log-priors
model.add(smp.exponential(sig),
smp.normal(b, mu=0, sig=100))
return model()
이 예제코드를 보면 $P(\beta, \sigma \mid D) $를 구하기 위해 model에 확률 분포를 add하였다.
이렇게 한 다음에 다음 코드를 실행한다.
start = smp.find_MAP(logp, {'b': np.ones(3), 'sig': 1.})
nuts = smp.NUTS(logp, start)
chain = nuts.sample(2100, burn=100)
smp.find_MAP는 위에서 설명한 대로 $P(\beta, \sigma \mid D)$를 구해서 가장 큰 확률을 갖는 $\beta,\sigma$를 찾는 과정이다. 내부 알고리즘을 살펴보지는 않으나 간단히 설명하면 다음을 구한다.
$\begin{aligned} & \log P(\beta, \sigma \mid D) \propto \log [P(D \mid \beta, \sigma) P(\beta) P(\sigma)] \\ & \log P(\beta, \sigma \mid D) \propto \log P(D \mid \beta, \sigma)+\log P(\beta)+\log P(\sigma)\end{aligned}$
log로 확률을 구하면 곱 대신 합으로 표현할 수 있기 때문에 비교적 간단하게 posterior distribution을 구하고 이를 maximize하도록 beta와 sigma를 최적화하면 된다.
이렇게 해서 구한 값은

다음과 같다. $\beta=[2,1,4]$인 과 비교할 때 거의 근접하게 찾은 것을 알 수 있다. 마찬가지로 $\sigma=1$인데 0.95정도로 비슷하게 구했다.
또한 NUTS(No-U-Turn Sampler)라는 Sampling 알고리즘을 통해 posterior distribution에서 sampling한 결과를 볼 수 있다.
plt.plot(chain.b)
plt.title('beta chain')
plt.xlabel('sample')
plt.show()
plt.plot(chain.sig)
plt.show()
import seaborn as sns
sns.histplot(chain.b)
plt.axvline(x=2,ymin=0, ymax=np.max(chain.b),color='black',linestyle='--', label='_nolegend_')
plt.axvline(x=1,ymin=0, ymax=np.max(chain.b),color='black',linestyle='--', label='_nolegend_')
plt.axvline(x=4,ymin=0, ymax=np.max(chain.b),color='black',linestyle='--', label='_nolegend_')
plt.legend(labels=[r'$\beta_0$',r'$\beta_{1}$',r'$\beta_{2}$'])
plt.show()
sns.histplot(chain.sig)
plt.title(r'$\sigma$')
plt.show()
$\beta$의 경우에는

histogram으로 보면 다음과 같다.

이 그래프를 역으로 생각하면, $\beta_{0}$의 경우 위의 예측값을 기준으로 분산이 얼마나 되는지를 가늠할 수 있다.
마찬가지로 $\sigma$의 경우에도
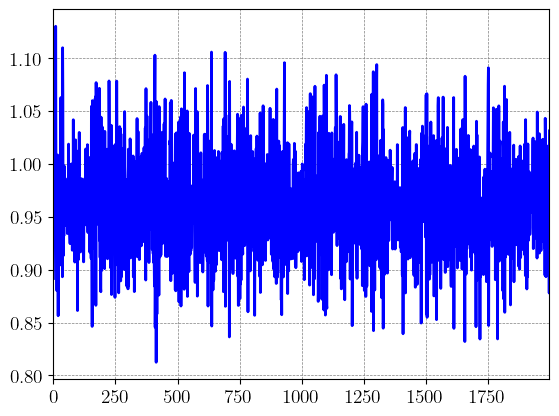
sample을 보면 위와 같고 이를 histogram으로 나타내면 아래와 같다.

위의 그림도 약 0.05만큼의 표준편차가 있는 것을 확인할 수 있다.
이런 식으로 내가 구하고 싶은 모델에 대한 uncertainty까지 확인 가능하다.
'연구 Research > 인공지능 Artificial Intelligent' 카테고리의 다른 글
| [JAX] Cholesky decomposition error 230318 기준 (0) | 2023.03.18 |
|---|---|
| [JAX] JAX vmap에 대한 설명 (0) | 2023.03.17 |
| [PyTorch] 개별 파라미터 learning rate 다르게 설정 및 learning rate 확인 (2) | 2023.03.05 |
| [JAX] Windows에서도 JAX 사용하기 (0) | 2023.02.24 |
| [에러기록] assertionerror: if capturable=false, state_steps should not be cuda tensors. (0) | 2023.02.23 |