맨날 Bayesian Neural Network (BNN)에 대해서 얘기를 듣다가 좋은 강의를 접하게 되어서 요약 정리하고 개별 내용을 보는 것이 어떨까 생각한다. 모든 자료들이 notation을 다르게 쓰다보니 따라가기 어려운 점이 있기도 하고..
만약 BNN 관련한 라이브러리를 한 번쯤 보신 분들이라면 MCMC, Dropout, Stein Variational Gradient Descent, Variational Inference 등 알 수 없는 용어들을 봤을 것이다. 필자도 배우는 단계이기 때문에 공부하면서 이 글이 수정될 수도 있다.
다루고 싶은 내용은
1) Bayesian Neural Network의 이론 기반
2) BNN에 포함되는 알고리즘
3) BNN Implementation (JAX 라이브러리 중심으로)
1. Bayesian Neural Network가 뭐지?
NN을 한 번 학습했다면 우리는 그 NN의 파라미터 값을 계속 쓰게 된다. 물론 중간중간마다 새로운 데이터가 들어오면 그 데이터를 위해 재학습을 하는 등의 일이 있을 수는 있지만 기본적으로 NN은 deterministic model로 정해진다.
여기서 사람들이 생각한 의문은 다음과 같다.
만약 입력 데이터가 기존에 학습한 데이터가 있을 때는 어떡하지? (데이터의 불확실성)
학습된 Neural Network의 uncertainty는 어떻게 알 수 있지? (모델의 불확실성)
이러한 의문은 합리적이다. 왜냐하면 우리가 아무리 데이터에 맞는 NN을 학습하더라도 새로운 입력에 대한 Uncertainty를 파악하지 못한다면 사람들이 그 모델을 실생활에 적용하기 어렵기 때문이다.
결국 NN의 파라미터를 확정하는 일은 우리가 이 모델의 파라미터를 Point estimate로 추정한다는 것과 같다. 그러나 사람들은 이 모델을 확률론적 관점에서, NN의 파라미터가 perturb될 때 어떤 결과가 나올지, 우리가 가지고 있는 입력과 출력 데이터가 있을 때 모델 파라미터는 어떤 확률 분포를 가지는지 알고 싶어했다. 그리고 만약 파라미터의 분포를 알고 있다면 새로운 입력 데이터가 주어질 때 계산되는 출력의 확률 분포도 알 수 있다.
- 모델의 확률 분포 : $p(\theta) \text{ where }\theta \text{: NN parameters}$
- 베이지안 관점에서 구한 posterior probability of NN parameters : $p(\theta \mid X,Y )=\dfrac{p(Y \mid X,\theta) P(\theta) }{P(Y\mid X)} =\dfrac{\text{likelihood}\times \text{prior}}{\text{evidence}}$
여기서 $X,Y$는 training dataset이다. - 새로운 입력($x_{*}$)이 주어질 때 출력의 확률 분포 : $p(y_{*} \min x_{*})=\int_{\theta}p(y \mid x_{*},\theta)p(\theta \mid X,Y)d\theta $
여기서 BNN이 구하고 싶어하는 것은 두번째 항목, a posterior distribution이다.
그러나 대부분의 문제는 이 posterior distribution을 구하기 어렵다는 데에서 나온다. 또한 posterior distribution을 간신히 구하더라도 내가 새로운 입력을 주어질 때의 출력 역시 모든 parameter에 대한 적분으로 표현되기 때문에 현실적으로는 구하기 어렵다는 문제가 존재한다. 그래서 도입된 유명한 방법들은 이들을 어떻게 tackle 할 것이냐의 문제이다.
NOTE1 : 나의 경우에는 이 a posterior distribution이라는 개념 자체가 와닿지 않았다. 모델 파라미터가 확률적으로 표현될 수 있다는 것이 어색하게 느껴졌던 것이다. 우리가 학습하고자 하는 NN 파라미터가 확률적이라는 것을 잊지 말아야 한다. 여기에서 NN을 우리가 생각하는 시스템, 모델이라고 생각하고 이 시스템은 입출력이 주어질 때 그 입출력을 최대한 잘 표현하는 시스템이라고 해보자. 그러면 이 시스템을 어떻게 학습해야할까? 그리고 학습된 확률적 모델은 어떻게 쓸 수 있을까?에 대해 고민하는 게 좋은 생각 흐름인 것 같다.
NOTE2: 사실 모델의 Uncertainty를 추정하는 방법은 꼭 Bayesian 관점에서만 있는 것은 아니다. 따라서 BNN을 공부하는 과정에서도 Non-Bayesian approach가 계속 따라오게 된다.
온갖 방법이 나오면 자꾸 까먹기 마련이므로 머릿 속에 계속 이 생각을 하면서 봐야 한다.
1) BNN / Posterior distribution을 구하는 방법
2) 이 구하는 방법들에 대한 근거
3) Uncertainty가 어떻게 도출되는지 / 출력($y_*$) 분포는 어떻게 결정되는지
내용을 이해하기 좋게 된 그림이 있어서 인용한다.
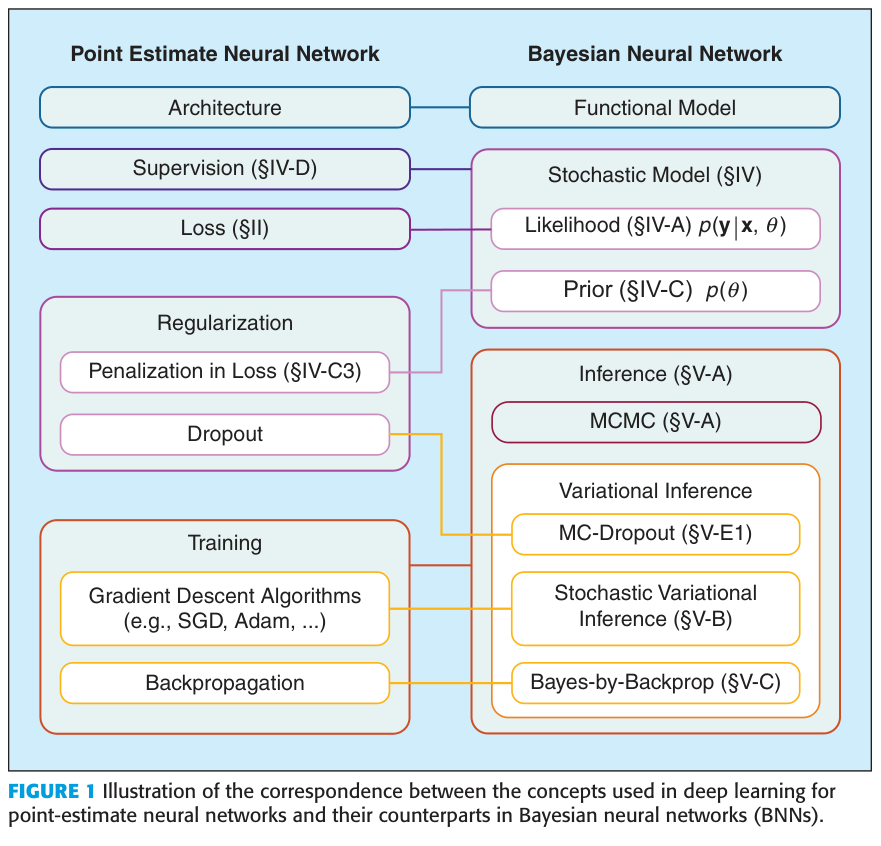
2. 방법들에 대한 scheme
1) Non-Bayesian Approach
Ensemble(bagging)과 boosting을 이용해서 Uncertainty를 정량화하는 방식
2) Bayesian Approach
Variational inference 방법론에 포함되는 알고리즘 : MC-Dropout, Stochastic variational inference (SVI) 등
앞으로 다룰 내용은 이런 알고리즘에 대한 간략한 내용들이다.

3. Aleatoric uncertainty & epistemic uncertainty
- Aleatoric uncertainty : 데이터 자체의 결함/노이즈로 인한 uncertainty
- Epistemic uncertainty : 모델에 대한 uncertainty / 더 많은 데이터를 통해 완화될 수 있다
Reference : What Uncertainties Do We Need in Bayesian Deep Learning for Computer Vision?
참고문헌 및 자료
edwith 최성준 교수님의 Bayesian deep learning 강의
논문 리스트 :
Jospin et al. Hands-on Bayesian Neural Networks - A tutorial for Deep Learning Users
https://neptune.ai/blog/bayesian-neural-networks-with-jax
'연구 Research > 인공지능 Artificial Intelligent' 카테고리의 다른 글
| [chatGPT] chatGPT 프롬프트 엔지니어링 (0) | 2023.11.28 |
|---|---|
| [JAX] L-BFGS optimizer로 학습하는 예제 코드 (0) | 2023.11.02 |
| [인공지능] Learning에서 scaling이 중요한가 (0) | 2023.09.20 |
| [JAX] vmap과 jit의 속도 (0) | 2023.09.20 |
| [인공지능] 인공지능 라이브러리 정리 (0) | 2023.08.24 |