빅데이터, 인공지능을 위한 수학에 대해서 정리합니다.
책은 The elements of Statistical Learning, Date Mining, Inference, and Prediction(Treveor Hastie 외 2명)을 참고할 것 같습니다.
수업을 들으면서 정리하는 내용이 주를 이룰 예정입니다.
제가 아직 확률 및 통계를 글로 정리하지는 않았지만 확률 및 통계 지식이 베이스로 있다고 생각하고 수업이 진행되기 때문에, 확률 및 통계 쪽 지식이 없으면 힘들 수도 있습니다. (저도 복습하면서 진행해야 할 것 같습니다ㅠ)
1. Probability와 관련된 용어
- Set : Given a certain condition, the collection of well-defined distinct objects
- Element : Object of a set
- Sample space($\Omega$) : Set of all possible results which can occur in a certain experiment
- Event : subset of a sample space
- $\sigma$-field, Event space ($\mathcal{F}$) : Set of subsets of the sample space
$\text{1. }\phi \in \mathcal{F}$
$\text{2. If }E_{1},E_{2},E_{3},\ldots\in\mathcal{F}\text{, then }\cup_{i}^{\infty}E_{i}\in\mathcal{F}$
$\text{3. If }E\in\mathcal{F}\text{, then }E^{c}\in\mathcal{F}$
예를 들어 주사위를 한 번 던지는 experiment가 있을 때
$\text{sample space = }\{1,2,3,4,5,6\}$
$\text{event space = }\{\phi, \{1\},\{2\},\cdots,\{1,2,3,4,5,6\}\}$
- Measure($\mu$) : function defined on $\mathcal{F}$ satisfying the following
$\mu(E)\geq0 \text{, for all }E\in\mathcal{F}$
$\mu{\phi}=0$
For any countable collection of pairwise disjoint set $\{E_{i}\}_{i=1}^{\infty}$
$\mu(\cup_{i=1}^{\infty}E_{i})=\sum_{i=1}^{\infty}\mu(E_{i})$
- Probability measure : Probability measure는 total measure가 1인 measure $\Rightarrow P(\Omega)=1$
- Probability space : $(\Omega, \mathcal{F}, P)$
- Joint probability($P(A\cap B)=P(A,B)$) : event A,B가 동시에 일어날 확률
- Conditional probability($P(A|B)$) : event B가 일어날 때 A가 일어날 확률 $P(A|B)=\frac{P(A\cap B)}{P(B)}$
- Independence : B가 A가 발생할 확률에 영향을 주지 않는 경우, A와 B는 independent.
$P(A|B)=P(A) \text{ if and only if }P(A\cap B)=P(A)P(B)$
2. Bayes theorem
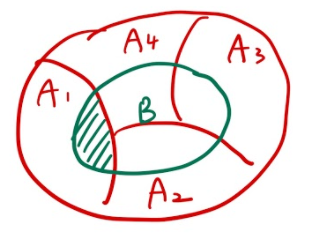
$P(A_{j}|B)=\frac{P(A_{j}\cap B)}{P(B)}=\frac{P(B|A_{j})P(A_{j})}{ \Sigma_{i=1}^{n} P(B|A_{i}) P(A_{i}) }$
이 공식은 Bayes naive classifier 등 다양한 머신러닝 알고리즘에 쓰입니다.
3. Random variable
Random variable : 확률에 따라 변하는 변수 (우리가 일반적으로 미적분에서 보는 변수variable은 deterministic variable입니다.)
event space 안에 존재하는 event들을 변수로 나타낸 것이라 이해할 수 있습니다.
$\text{When the image of X is countable, for every real value a, }(-\infty,a)^{-1}=\{\omega|X(\omega<a)\}\in\mathcal{F}$
Random variable X가 a보다 작은 event $\omega$를 모아놓은 것에 대해 $(-\infty,a_{1})^{-1}$라고 표현합니다.
Random vector $X=(X_{1},X_{2},\ldots,X_{d})$
이 Random vector는 Vector function defined on $\Omega$입니다.
$\text{For every real number }a_{1},a_{2},\ldots,a_{d}, (-\infty,a_{1})\times\cdots\times(-\infty,a_{d})^{-1}=\{\omega|X_{1}(\omega)<a_{1},\ldots,X_{d}(\omega)<a_{d}\}\in\mathcal{F}$
$P(X\in A) := P(\{\omega|X(\omega)\in A\})$
Discrete random variable : when the image of X is countable
Continuous random variable : when the image of X in uncountable
4. Distribution function
- Cumulative Distribution function, $F_{x}$ 누적분포함수
- Discrete random variable : Probability Mass Function, $p_{x}$ 확률질량함수
- Continuous random variable : Probability Density Function, $f_{x}$ 확률밀도함수
5. Expectation(Mean), Variance, Covariance
Expectation(Mean, 평균) $E, \mu$
Expectation of Discrete random variable : $\Sigma_{x}xp_{x}$
Expectation of Continuous random variable : $\int_{x}xf_{x}dx$
Variance (분산) $\sigma^{2}$
$\sigma^{2}=E((X-\mu)^{2})=E(X^{2})-\mu^{2}$
Covariance (공분산)
$X=(X_{1},\ldots,X_{n})^{T}$이 random vector일 때
random variable 간의 variance matrix를 만들 수 있습니다.
$\text{Covariance matrix }\sigma^{2}=(\sigma_{i,j})$
$\sigma^{2}=E((X-\mu)(X-\mu)^{T})\Rightarrow \sigma_{i,j}=E((X_{i}-\mu_{i})(X_{j}-\mu_{j}))$
6. Distribution 종류
Discrete distribution
1. Bernoulli distribution
2. Geometric distribution
3. Binomial distribution
4. Poisson distribution
Continuous distribution
1. Normal(Gaussian) distribution
2. $\chi^{2}$-distribution
3. Student's T-distribution
4. F-distribution
7. Basic Limit Theorems
1) Law of Large Number, LLN 큰 수의 법칙
동일한 확률 분포를 가진 independent random variables $X_{1},X_{2},\ldots,X_{n},\ldots$가 있을 때 sample mean은 population mean으로 수렴합니다.
2) Central Limit Theorem
동일한 확률 분포(mean $\mu$, variance $\sigma^{2}$)의 independent n random variables의 mean distrbution은 n이 충분히 클 때 normal distribution에 가깝다.
$\frac{\sqrt{n}}{\sigma}(\bar{X}-\mu)\rightarrow Z$
대부분의 경우에는 population variance를 모르기 때문에 $\sigma$ 대신 sample variance를 써서 사용합니다.
'연구 Research > 인공지능 Artificial Intelligent' 카테고리의 다른 글
| [머신러닝] Boosting method (0) | 2021.05.26 |
|---|---|
| [머신러닝] Logistic Regression (0) | 2021.05.25 |
| [머신러닝] Classification evaluation measure (0) | 2021.05.25 |
| [머신러닝] Decision Tree (0) | 2021.05.25 |
| [머신러닝] Unsupervised learning : Clustering (0) | 2021.05.25 |