이번에는 explicit euler 방법이 아닌 implicit euler 방법을 사용하고자 합니다.
# Notation 참고
$x_{B}^{A}$ : $A$는 시간에서의 위치(Timesteps), $B$는 공간에서의 위치를 의미합니다.
$y^{'}=f(y,t)$
model problem인 $y^{'}=\lambda y$을 implicit euler 방법으로 풀어보겠습니다.
$\frac{y^{n+1}-y^{n}}{\Delta t}=f(y^{n+1},t^{n+1})$ : implicit euler이므로 현재 y,t값이 아닌 미래의 값(n+1)을 사용합니다.
$\frac{y^{n+1}-y^{n}}{\Delta t}=\lambda y^{n+1} \Rightarrow y^{n+1}-\lambda \Delta t y^{n+1}=y^{n}$
$y^{n+1}=\frac{1}{1-\lambda \Delta t}y^{n}=\sigma y^{n}$
$y^{n}=\sigma^{n}y^{0}$
1) Accuracy
$\text{Implicit euler : }\sigma = \frac{1}{1-\lambda \Delta t}=1+\lambda \Delta t+\lambda^{2}\Delta t^{2}+\cdots$
$\text{Exact : }\sigma^{\lambda \Delta t}=1+\lambda \Delta t +\frac{1}{2}\lambda^{2}\Delta t^{2}+\cdots$
두 개를 비교하면 그 errors는 second order in a time step입니다. globally first order accuracy.
2) Stability
$\sigma = \frac{1}{1-\lambda \Delta t}=\frac{1}{1-\lambda_{R}\Delta t -i\lambda_{I}\Delta t}$
$|\sigma|=\left | \frac{1}{1-\lambda_{R}\Delta t -i\lambda_{I}\Delta t} \right |<1 \text{ for }\forall \lambda_{R}\leq 0$
앞서 explicit euler에서처럼 amplication factor가 1보다 작아야 stable solution을 얻을 수 있습니다.
위 조건에 맞는 영역은

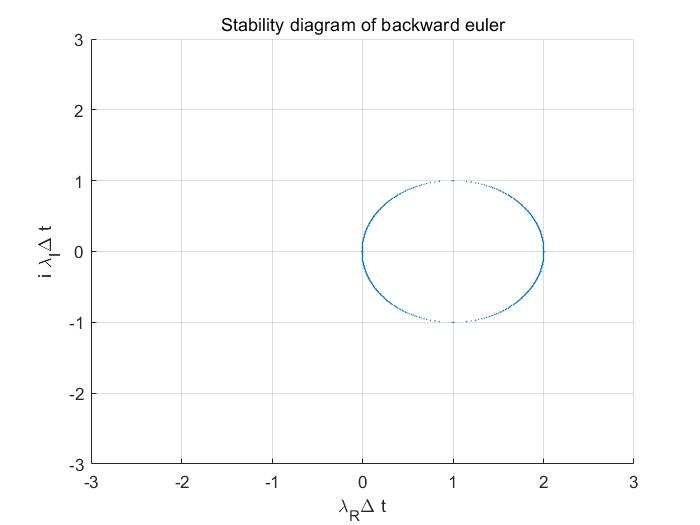
$\lambda_{R}h<0$일 때 implicit euler 방법을 쓰면 항상 solution이 stable하므로, implicit euler는 Absolutely stable(A-stable)입니다.
$\lambda_{R}h>0$인 영역은 원래 unstable system이므로 고려하지 않지만, 만약 unstable한 문제를 풀 때도 위 그림처럼 stable한 solution이 나온다면 문제가 될 수도 있습니다.
3) Phase error & amplitude error
이전 explicit euler때처럼 $\lambda = i\omega$일 때 phase error와 amplitude error를 알아보겠습니다.
$\text{Implicit euler : }\sigma = \frac{1}{1-i\omega \Delta t}=\frac{1+i\omega\Delta t}{1+\omega^{2}\Delta t^{2}}$
$|\sigma|^{2}=\frac{1}{1+\omega^{2}\Delta t^{2}}<1$
stability diagram을 통해 알 수 있듯이 pure imaginary에서 implicit euler는 decaying합니다.
또한 phase error = $\theta = \tan^{-1}\frac{Im(\sigma)}{Re(\sigma)}=\tan^{-1}\omega \Delta t=\omega\Delta t-\frac{(\omega \Delta t)^{3}}{3}+\cdots$
exact값은 $\omega \Delta t$이므로
$\text{Phase error }=\omega \Delta t-\theta = \frac{(\omega \Delta t)^{3}}{3}$
4) Implicit euler의 특징
larger memory space is needed
flexbility in time-step
nonlinear equation에 대해서 iteration이 필요함
5) Explicit euler와 비교
model problem에 대해서
$\text{exact : }y=y^{0}e^{\lambda t}=(e^{\lambda \Delta t})^{n}y^{0} \Rightarrow \sigma_{exact}=e^{\lambda \Delta t}$
$\text{explicit euler : }y=(1+\lambda \Delta t)^{n}y^{0} \Rightarrow \sigma_{ee}=1+\lambda \Delta t$
$\text{implicit euler : }y=\left (\frac{1}{1-\lambda \Delta t}\right)^{n}y^{0} \Rightarrow \sigma_{ie}=\frac{1}{1-\lambda \Delta t}$
둘은 same order of accuracy를 가졌지만 부호가 다릅니다.

implicit euler는 explicit euler와 다르게 A-stable이지만 실제 사용하기에는 accuracy order가 낮다는 단점을 가지고 있습니다.
'수치해석 Numerical Analysis' 카테고리의 다른 글
| [수치해석] Numerical solution of ODE (5) Predictor-Corrector Method (0) | 2021.09.26 |
|---|---|
| [수치해석] Numerical solution of ODE (4) Trapezoidal method (Crank-Nicolson) (0) | 2021.09.24 |
| [수치해석] Numerical solution of ODE (2) Explicit Euler (0) | 2021.04.27 |
| [수치해석] Numerical solution of ODE (1) introduction (0) | 2021.04.07 |
| [수치해석] Numerical integration (3) - Gauss quadrature (0) | 2021.04.04 |