(앞선 글부터 보면 알 수 있지만 문자를 표현할 때 아래 첨자는 공간 상의 좌표, 위 첨자는 시간 상의 좌표를 의미합니다.)
trapezoidal 방법은 implict method 중 하나입니다. (즉, 미분할 때 다음 값($y^{n+1},t^{n+1}$)도 가져다 씀)
이 방법은 PDE에 쓰일 때 Crank-Nicolson method라고 합니다.
$y^{'}=f(y,t)$
$\frac{y^{n+1}-y^{n}}{\Delta t}=\frac{1}{2}\left[f(y^{n},t^{n})+f(y^{n+1},t^{n+1})\right]$
implicit이면 stable 영역에서 항상 stable합니다. 위 방법의 장점은 accuracy가 globally 2nd order($\Delta t^{2}$)라는 점입니다.
이 방법을 model problem을 통해 분석해보겠습니다.
$y^{'}=\lambda y$
$\frac{y^{n+1}-y^{n}}{\Delta t}=\lambda\left(\frac{1}{2} y^{n}+\frac{1}{2} y^{n+1}\right)$
$y^{n+1}-\frac{\lambda \Delta t}{2} y^{n+1}=y^{n}+\frac{\lambda \Delta t}{2} y^{n}$
$y^{n+1}=\left(\frac{1+\frac{\lambda \Delta t}{2}}{1-\frac{\lambda \Delta t}{2}}\right) y^{n} \rightarrow y^{n}=\left(\frac{1+\frac{1 \Delta t}{2}}{1-\frac{\lambda \Delta t}{2}}\right)^{n} y^{0}$
여기서 각 iteration마다 amplication factor인 $\sigma_{TR}$가 곱해져서 y값을 구하게 됩니다.
$y^{n}=\sigma_{TR}^{n} y^{0}$
$\sigma_{TR}=\frac{1+\frac{\lambda \Delta t}{2}}{1-\frac{\lambda \Delta t}{2}}$
이 값을 $\sigma_{exact}$와 비교를 하면 accuracy, phase error, stability를 알 수 있습니다.
1. Accuracy
$\sigma_{\text {exact }}=e^{\lambda \Delta t} = 1+\lambda \Delta t+\frac{(\lambda \Delta t)^{2}}{2!}+\frac{(\lambda \Delta t)^{3}}{3!}+\cdots$
$\sigma_{TR}=\left(1 + \frac { \lambda \Delta t } { 2 } \right) / \left(1 - \frac { \lambda \Delta t } { 2 }\right) =1 + \lambda \Delta t + \frac { ( \lambda \Delta t ) ^ { 2 } } { 2 } + \frac { ( \lambda \Delta t ) ^ { 3 } } { 4 } + \cdots$
두 항을 비교하면 $\Delta t^{3}$일 때부터 차이가 나므로 locally 3rd order accuracy를 가지고 globally 2nd order입니다. (적분하면 $\Delta t$만큼 곱해지므로)
2. Stability
stability는 시스템의 eigenvalue에 따라서 stable한 시스템일 때 amplication factor의 절댓값이 1을 넘으면 시간이 거듭할 수록 값이 발산하게 됩니다. 따라서 $|\sigma_{TR}|$의 절댓값이 1보다 작은 영역을 확인합니다.
$\lambda=\lambda_{R}+i \lambda_{I}$
$\sigma_{T R}=\left|\frac{\left(1+\frac{\lambda_{R} \Delta t}{2}\right)+i\left(\frac{\lambda_{1} \Delta t}{2}\right)}{\left(1-\frac{\lambda_{R} \Delta t}{2}\right)-i\left(\frac{\lambda_{1} \Delta t}{2}\right)}\right| \leqslant 1$


(MATLAB으로 $|\sigma|<1$인 영역의 경계를 표시해놓은 것입니다. (왼쪽 경계는 식을 대입한 x범위 때문입니다. 적어도 $-3<\lambda_{R}\Delta t<0$에서는 1보다 작습니다.)
trapezoidal method의 장점은 다음과 같이 exact solution과 동일한 stability 영역을 갖는다는 점입니다.
따라서 시스템이 unstable하면 trapezoidal method로 답을 구했을 때 똑같이 unstable하게 나오고, 시스템이 stable하면 동일하게 stable한 결과를 얻을 수 있습니다. 즉, 이 방법은 A-stable(Unconditionally stable)합니다.
3. Phase error
phase error는 $\lambda=i\omega$라고 생각하고 oscillating system에 대해 위상차가 얼마나 변하는지 알아보는 것입니다. $\sigma_{TR}$식에서 $\lambda=i\omega$만 대입해주면 됩니다.
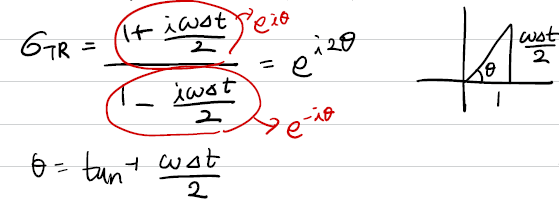
여기서 $2\arctan(\omega\Delta t /2)$가 trapezoidal method를 사용했을 때 나오는 phase입니다.
exact $\theta=\omega \Delta t$와 얼마나 차이가 나는지 계산해보면
$\text{Phase error }= \omega \Delta t-2 \tan ^{-1} \frac{\omega \Delta t}{2}=+\frac{1}{12}(\omega \Delta t)^{3}$
이전에 봤던 implicit euler 방법에서 phase error가 $\frac{(\omega \Delta t)^{3}}{3}$이므로 trapezoidal method의 phase error가 더 작습니다.
explicit euler 방법은 $\Delta t$의 크기가 한정되지만(unstable한 영역 때문에)
trapezoidal method나 implicit euler(backward euler) 방법은 $\Delta t$가 한정되지는 않습니다.
다만 $\Delta t$가 너무 크면
$ \underset{\Delta t \rightarrow \infty}{\lim}\sigma_{TR}=-1$이므로
solution 값이 심하게 진동하기 때문에 $\Delta t$가 너무 크지 않은지 확인할 필요가 있습니다.

다음 그림은 Implicit Euler(그림에서 IE) 방법, Explicit Euler(그림에서 EE) 방법, Trapezoidal 방법을 비교했습니다.
위 시스템은 oscillating만 하는 시스템입니다. (eigenvalue에서 imaginary 성분 밖에 없음)
이 때 trapezoidal은 amplitude 변화없이 phase 차이만 존재하고,
IE 방법은 점점 amplitude가 감소하고, EE방법은 점점 amplitude가 커지는 것을 확인할 수 있습니다. phase error 차이는 는 그림에서 잘 표현되지 못했으니 자세한 것은 이전 글을 찾아봐주세요. 둘의 phase error가 동일한데 그림을 그릴 당시에는 그걸 표현하지 못했네요.
Trapezoidal method는 여기까지 하고 다음에는 explicit method 중 하나인 Predictor-Corrector method를 보겠습니다.
'수치해석 Numerical Analysis' 카테고리의 다른 글
| [수치해석] Numerical solution of ODE (6) Runge-Kutta method (0) | 2021.09.26 |
|---|---|
| [수치해석] Numerical solution of ODE (5) Predictor-Corrector Method (0) | 2021.09.26 |
| [수치해석] Numerical solution of ODE (3) Implicit Euler (Backward Euler) (0) | 2021.04.29 |
| [수치해석] Numerical solution of ODE (2) Explicit Euler (0) | 2021.04.27 |
| [수치해석] Numerical solution of ODE (1) introduction (0) | 2021.04.07 |