옛날부터 automatic differentiation을 보면서 용어가 잘 정리가 안되었는데 이번 기회에 정리를 하고자 한다.
automatic differentiation만 궁금하다면 이 글을 봐도 좋지만 적절한 맥락을 알고 싶다면 다음 글을 참고하면 좋을 것이다.
이 글에서 다루는 키워드는 다음과 같다.
Automatic differentiation (AD) Forward mode
Automatic differentiation (AD) Reverse mode
여기에 더해서 JAX에서 자주 나오는 용어인 Jacobian-vector-product (JVP)와 Vector-Jacobian-product (VJP)에 대해서도 다룬다.
1. Chain rule
AD란 수치적으로 derivative를 구하는 방법 중 하나이다. 이 때 symbolic rules for differentiation을 써서 일반적으로는 finite difference approximation보다 더 정확하다고 알려져있다. 그러나 실제로 쓸 때는 심볼릭 계산을 쓰기 보다는 계산할 당시에 수치적으로 미리 계산해서 나중에 측정 값의 derivatives를 구하는 식으로 사용된다.
여기에서 두 방법이 있는데
1) Forward mode
2) Reverse mode
다음과 같다.
2. Forward mode & Reverse mode
다음과 같은 연속적인 함수들이 있다고 하자.
\[ y = f(x) = \sin(\exp(x^2)) = l(m(n(x))) \]
\[ \begin{aligned} z^{[0]} &= x \\ z^{[1]} &= n(z^{[0]}) = (z^{[0]})^2 \\ z^{[2]} &= m(z^{[1]}) = \exp(z^{[1]}) \\ z^{[3]} &= l(z^{[2]}) = \sin(z^{[2]}) \\ y &= z^{[3]} \end{aligned} \]
입력은 $x$이고 출력은 $y$이다.
우리는 $x$에 대한 $y$의 변화율을 알고 싶다고 하자.
$$\frac{\partial y}{\partial x} =\frac{\partial y}{\partial z^{[3]}} \frac{\partial z^{[3]}}{\partial z^{[2]}} \frac{\partial z^{[2]}}{\partial z^{[1]}} \frac{\partial z^{[1]}}{\partial z^{[0]}} \frac{\partial z^{[0]}}{\partial x} \frac{\partial y}{\partial x} $$
이런 chain rule을 적용해서 계산을 할 수 있다. 하지만 이 때 중요한 것이 계산 순서이다.
다음과 같이 계산하면 forward mode라고 한다.
$$\frac{\partial y}{\partial x}= \underbrace{\frac{\partial y}{\partial z^{[3]}} \left( \frac{\partial z^{[3]}}{\partial z^{[2]}} \left( \frac{\partial z^{[2]}}{\partial z^{[1]}} \left( \frac{\partial z^{[1]}}{\partial z^{[0]}} \frac{\partial z^{[0]}}{\partial x} \right) \right) \right) }_{\text{forward-mode}}$$
$$ \frac{\partial y}{\partial x} = \underbrace{ \left( \left( \left( \frac{\partial y}{\partial z^{[3]}} \frac{\partial z^{[3]}}{\partial z^{[2]}} \right) \frac{\partial z^{[2]}}{\partial z^{[1]}} \right) \frac{\partial z^{[1]}}{\partial z^{[0]}} \right) \frac{\partial z^{[0]}}{\partial x} }_{\text{reverse-mode}} $$
즉, 계산순서가 다르다. 왜 이게 이점이 될까?
입력과 출력이 모두 스칼라이고 내부 계산이 평이한 경우에는 큰 문제가 없을 수 있다.
하지만, 일반적으로 자코비안(Jacobian)은 sparse matrix인 경우가 많고, 인공신경망과 같이 내부 operation 상에서 자코비안이 $N \times N \; (N>>1)$인 경우에는 계산이 매우 비효율적이게 된다.
위에서는 Forward mode, reverse mode에 대해 설명했지만 실제로 이걸 어떻게 implement했는가는 또 생각할 부분이다. 여기서는 자세히 다루지 않고 MATLAB에 있는 설명을 간단히 이야기하고자 한다.
다음과 같은 $$f(x)=x_1 \exp{ -\frac{1}{2} (x_1^2 +x_2^2)}$$ 계산이 있을 때 $\frac{d f}{d x}$를 계산하고 싶다고 하자.

Chain rule을 사용한다면 다음과 같이 계산할 수 있다.
$$
\begin{aligned}
\frac{df}{dx_1} &= \frac{du_6}{dx_1} \\
&= \frac{du_6}{du_{-1}} + \frac{\partial u_6}{\partial u_5} \frac{\partial u_5}{dx_1} \\
&= \frac{du_6}{du_{-1}} + \frac{\partial u_6}{\partial u_5} \frac{\partial u_5}{\partial u_4} \frac{\partial u_4}{dx_1} \\
&= \frac{du_6}{du_{-1}} + \frac{\partial u_6}{\partial u_5} \frac{\partial u_5}{\partial u_4} \frac{\partial u_4}{\partial u_3} \frac{\partial u_3}{dx_1} \\
&= \frac{du_6}{du_{-1}} + \frac{\partial u_6}{\partial u_5} \frac{\partial u_5}{\partial u_4} \frac{\partial u_4}{\partial u_3} \frac{\partial u_3}{\partial u_1} dx_1.
\end{aligned}
$$
Forward mode에서 gradient 값을 계산하기 위해서는 일단 먼저 함수를 한 번 evaluation을 거치고, 그 다음에 아래와 같은 $x_1$에 대한 $f$의 미분을 위해 그래프를 한 번 더 거쳐야 한다. 여기서 지적할 수 있는 부분은 $x_2$에 대한 gradient를 계산하고 싶은 경우에도 비슷한 computational graph를 거쳐야 한다는 것이다. 즉, the gradient of the function을 위해서는 graph를 거쳐야 하는 횟수가 변수의 개수와 동일하다. 이는 일반적인 deep learning(입력의 차원이 크고, 출력의 차원이 작은 경우)에서는 매우 느리다. 그러나 중간 계산 과정을 저장할 필요가 없기 때문에 메모리가 덜 필요하다.
reverse mode의 경우에는 다음과 같은 adjoint variables를 상정한다.
$$\bar{u}_i = \frac{\partial f}{\partial u_i}$$
이 변수는 기존 변수 위에 bar를 추가해서 표기한다.
\[
\begin{aligned}
\frac{\partial f}{\partial u_{-1}} &= \frac{\partial f}{\partial u_1} \frac{\partial u_1}{\partial u_{-1}} + \frac{\partial f}{\partial u_6} \frac{\partial u_6}{\partial u_{-1}} \\
&= \bar{u}_1 \frac{\partial u_1}{\partial u_{-1}} + \bar{u}_6 \frac{\partial u_6}{\partial u_{-1}}.
\end{aligned}
\]
위 계산을 보고 $u_1 = u_{-1}^2$ and $u_6 = u_5 u_{-1}$라는 것을 이미 알고 있다.
\[
\bar{u}_{-1} = \bar{u}_1 2u_{-1} + \bar{u}_6 u_5.
\]
따라서 adjoint variable $\bar{u}_{-1}$는 위 식을 통해 구할 수 있다. 이런 식으로 adjoint variable들에 대한 관계식이 나온다.
이 adjoint variable을 유도하는 과정은 손으로 적어서 첨부한다.

처음 함수를 evaluation할 때 이 중간 변수를 저장하고 있다가 최초의 adjoint variable(아래 그림의 seed) $\bar{u}_6$에서 시작해서 차근차근 계산하면
다음과 같이 함수의 입력 $x_1,x_2$에 대한 gradient를 한 번에 구할 수 있다.
$\bar{u}_0 = \frac{\partial f}{\partial u_0} = \frac{\partial f}{\partial x_2}$ and $\bar{u}_{-1} = \frac{\partial f}{\partial u_{-1}} = \frac{\partial f}{\partial x_1}$.

MATLAB 설명에서는 reverse mode가 더 효율적이라고 나와있는데 항상 그런 건 아니다. 본인의 어플리케이션에 따라 달라질 수 있다. 적어도 신경망 학습에 있어서는 reverse mode가 효율적이라고 알려져있다.

이제 위 내용을 이해했다면 JVP와 VJP, Pullback과 Pushforward에 대해서도 이해한 셈이다.
JVP (Jacobian Vector Product) = Pushforward = forward
VJP (Vector Jacobian Product) = Pullback = reverse mode
프로그래밍 언어나 라이브러리마다 이를 칭하는 이름은 다르지만 위의 용어들이 같다는 것을 인식해야 한다.
3. JVP (Jacobian Vector Product) and Vector Jacobian Product (VJP)
1) Jacobian Vector Product
주어진 함수는 $f:\mathbb{R}^{n}\rightarrow \mathbb{R}^{m}$, the Jacobian of $f$ evaluated at an input point $x\in \mathbb{R}^n =: \partial f(x)$를 구해야 한다고 하자.
이 때, $\partial f(x)$는 $\mathbb{R}^{m\times n}$ 형태이다. (수학 convention에 따라 조금씩 다를 수 있기는 하지만 기본적으로 multivariate vector function을 다룰 때 인공지능 분야에서는 이렇게 정의한다.)
$\partial f(x)$를 해석하자면 linear map, point $x$에서 $f$의 domain 상의 $tangent space$에서 point $f(x)$에서 $f$의 codomain의 tangent space로 mapping하는 것으로 이해할 수 있다.
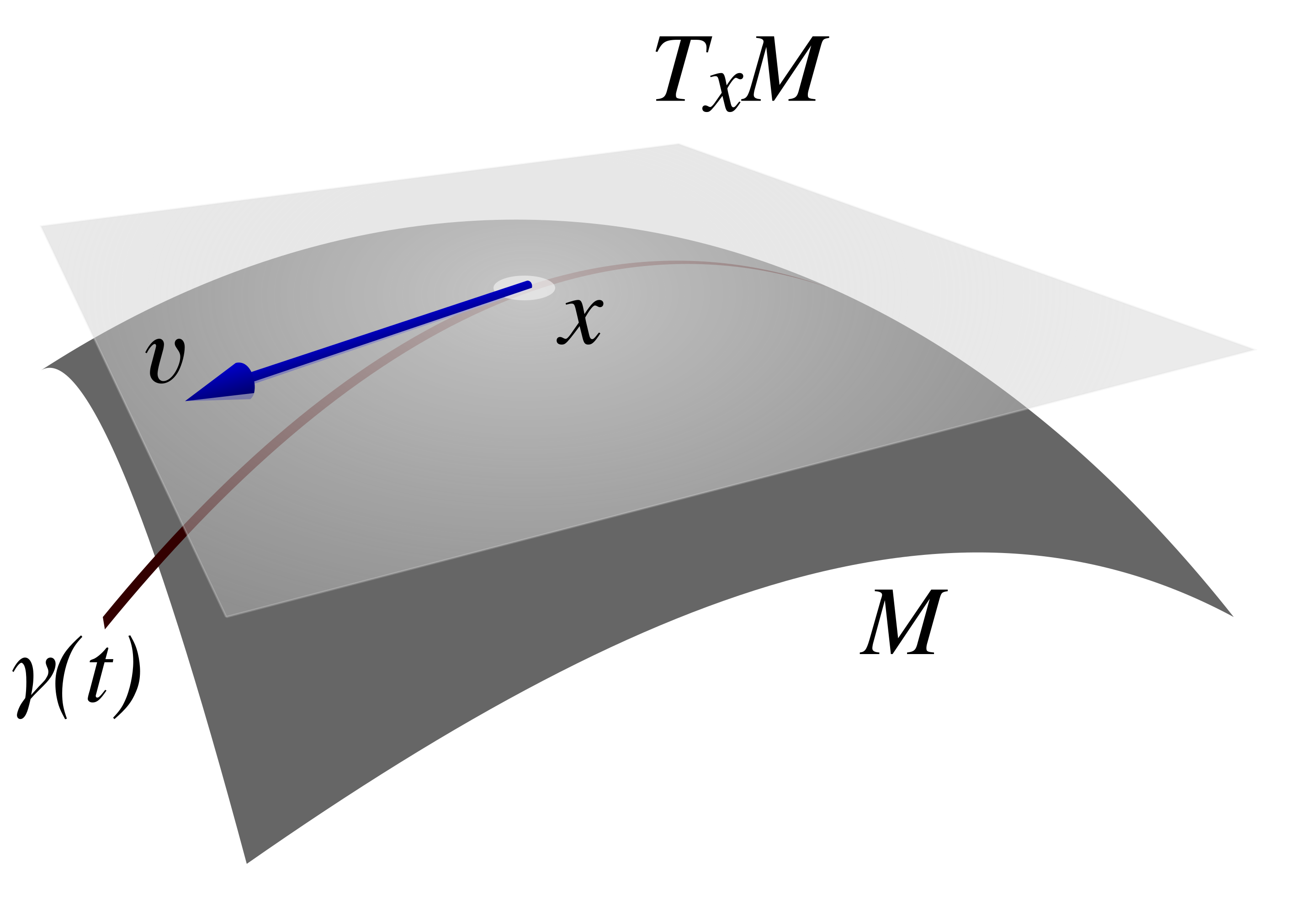
$\partial J(x):\mathbb{R}^{n} \rightarrow \mathbb{R}^m$
이러한 map을 pushforward map of $f$ at $x$라고 한다.
잘 생각해보면 $x^*$가 주어졌을 때 그 $x^*$에 대한 vector function의 $\partial f(x^*) \in \mathbb{R}^{m\times n}$가 계산된다. 이 말은 곧,
$$\partial f : \mathbb{R}^n \rightarrow \mathbb{R}^{n} \rightarrow \mathbb{R}^m$$
다음과 같이 a given input point $x^* \in \mathbb{R}^n$, a tangent vector $v \in \mathbb{R}^n$이 주어질 때 an output tangent vector $\mathbb{R}^m$를 얻을 수 있다는 뜻이다. 이 말이 무슨 뜻인가?
우리가 어떤 포인트($x^*$)에서의 함수의 변화율($\partial f(x)$)를 구했다고 하자. 그러면 그 때의 자코비안을 알 수 있다. 우리가 원하는 것은 내가 $v$만큼 변할 때의 $f$의 변화량을 알고 싶은 것이다.
대부분의 문제들은 함수의 자코비안을 구하는 것이 아니라, $\partial f(x) v$값을 알고 싶어한다. 이는 굉장히 중요한데, 단순 $\partial f(x)$를 따로 구해서 $\partial f(x) v$를 구하는 것보다 $\partial f(x) v$ 자체를 구하는 것이 더 효율적이기 때문이다.
그래서 이렇게 $(x,v)$ pair에서 output tangent vectors로 mapping하는 것을 "Jacobian-vector product"라고 한다.
$(x,v) \mapsto \partial f(x) v$ ($\partial f(x)$가 Jacobian이고 $v$가 vector이기 때문에 JVP라고 부른다.
그래서 다음과 같은 코드에서는
from jax import jvp
# Isolate the function from the weight matrix to the predictions
f = lambda W: predict(W, b, inputs)
key, subkey = random.split(key)
v = random.normal(subkey, W.shape)
# Push forward the vector `v` along `f` evaluated at `W`
y, u = jvp(f, (W,), (v,))
$y$는 주어진 $x$에서 evaluate한 값인 $f(x)$를 의미하고, $u$는 $\partial f(x)v$를 의미한다. JVP 방법은 forward mode와 마찬가지로 계산하면서 JVP를 evaluate하기 때문에 필요한 메모리는 depth of computation에 따라 다르다.
신경망 학습 시 이 방법의 단점:
Full jacobian matrix를 얻기 위해서는 각 $v$를 one-hot tangent vector로 설정한 다음에 각각 얻은 jacobian의 한 column을 이어붙여서 전체 jacobian matrix를 만든다. 그러면 인공신경망 같이 파라미터 수가 굉장히 많은 시스템은
$\partial f(x)\in \mathbb{R}^{1\times n}$를 계산하기 위해 엄청나게 많은 반복을 해야한다. 따라서 이럴 때는 VJP를 쓰는 게 더 유리하다.
2) Vector Jacobian Product
동일한 $f:\mathbb{R}^{n}\rightarrow \mathbb{R}^{m}$에서
$$(x,v) \mapsto v\partial f(x)$$
다음과 같이 mapping하는 것이다.
$v$는 an element of the cotangent space of $f$ at $x$이다.
다르게 표현하면
$$(x,v) \mapsto \partial f(x)^{\top} v$$
$$\partial f(x)^{\top} : \mathbb{R}^{m} \rightarrow \mathbb{R}^n$$와 같다. 이 map을 pullback of $f$ at $x$라고 한다.
이제 앞에서 봤던 JVP와 VJP를 비교해보자. 결국 동일하게 Jacobian을 구하는 것이지만 최종적으로 얻게 되는 output vector의 차원이 다르다는 것을 알 수 있다. 이는 마치 우리가 $f$의 output에 주목하던 것에서 input에 주목하는 것으로 볼 수 있다. 또한 앞서서 신경망을 학습할 때 JVP를 쓸 때 한 column씩 계산했던 것을 돌이켜볼 때, VJP는 row씩 계산하기 때문에 입력 parameter의 차원이 클 때 더 유리하다는 것을 알 수 있다. 그래서 VJP를 gradient 구할 때 쓸 수 있다.
여기서 forward-mode와 reverse-mode를 JAX에서 어떻게 구현했는지에 대해서는 설명을 줄였는데 더 깊게 알아보고 싶으면 다음 링크를 참고하라고 하니, 나중에 듣고 정리해볼 생각이다.
참고자료
https://www.youtube.com/watch?v=N7nVoyR0qO4&list=PLISXH-iEM4JkjRcfN6gNCRY74FlgQ1Anb
Automatic Differentiation Background
You clicked a link that corresponds to this MATLAB command: Run the command by entering it in the MATLAB Command Window. Web browsers do not support MATLAB commands.
www.mathworks.com
'연구 Research > 인공지능 Artificial Intelligent' 카테고리의 다른 글
| [연구] SciML 분야 라이브러리 기록 (0) | 2024.03.11 |
|---|---|
| [chatGPT] chatGPT 프롬프트 엔지니어링 (0) | 2023.11.28 |
| [JAX] L-BFGS optimizer로 학습하는 예제 코드 (0) | 2023.11.02 |
| [Deep learning] Bayesian Neural Network (1) (0) | 2023.10.23 |
| [인공지능] Learning에서 scaling이 중요한가 (0) | 2023.09.20 |