이번에는 수치해석에서 사용하는 interpolation 방법에 대해서 알아봅니다.
우리의 목적은 주어진 discrete data $(x_{i},y_{i})\text{ for }i=1,2,3,\ldots, n$가 있을 때
두 데이터 points 사이에 있는 point의 value y를 구하고 싶은 것입니다.
또한 우리는 $f^{'},f^{''}, \text{ or }\int f dx$도 알고 싶습니다.
(위에서 $f^{''}$까지 요구하는 이유는, 보통 기계공학에서 일반적인 DE는 order가 2nd order DE이므로, 두 번 미분한 값까지 아는 것이 좋기 때문입니다.)
주어진 데이터 안에서 알지 못하는 x에 대한 y값을 알 수 있는 방법은, 주어진 데이터를 가지고 시스템의 함수식을 예측해보는 방법이 있을 것입니다.
그 함수에 우리가 궁금한 y값에 해당하는 x값을 대입해보는 것입니다.
이 때 두 가지 방법이 있는데
1) find a smooth curve through the data
2) find a smooth curve pass through all the data
그림 출처 : en.wikipedia.org/wiki/Least_squares#/media/File:Linear_least_squares2.svg
1)의 경우는 least square method를 이용해 curve fitting하는 것을 생각할 수 있습니다. 그러나 수치해석에서는 논의하지 않습니다.
2)의 경우만 생각해서 주어진 데이터에 맞는 curve를 구하고, 이를 이용해 interpolation하는 방법을 살펴보겠습니다.
1. Polynomial interpolation
$(x_{i},y_{i})$ $i=1,2,3,\ldots,n$ : 총 n개의 points를 데이터로 가지고 있습니다.
$P(x) = a_{0}+a_{1}x^{1}+a_{2}x^{2}+\cdots+a_{n-1}x^{n-1}$
이 n개의 points를 가지고 (n-1)차 polynomial을 만들고자 합니다.
미지수(Unknowns)는 $a_{0},\ldots,a_{n-1}$ 총 n개입니다.
$\left\{\begin{matrix}
P(x_{1})=y_{1}=a_{0}+a_{1}x_{1}+a_{2}x_{1}^{2}+\cdots+a_{n-1}x_{1}^{n-1}&\text{when }i=1\\
P(x_{2})=y_{2}=a_{0}+a_{1}x_{2}+a_{2}x_{2}^{2}+\cdots+a_{n-1}x_{2}^{n-1}&\text{when }i=2\\
\vdots \\
P(x_{n})=y_{n}=a_{0}+a_{1}x_{n}+a_{2}x_{n}^{2}+\cdots+a_{n-1}x_{n}^{n-1}&\text{when }i=n
\end{matrix}\right.$
위의 방정식을 matrix로 바꾸면 다음과 같습니다.
$\begin{bmatrix}
1 & x_{1} & x_{1}^{2} & \cdots & x_{1}^{n-1} \\
1 & x_{2} & x_{2}^{2} & \cdots & x_{2}^{n-1} \\
\vdots & & & & \\
1 & x_{n} & x_{n}^{2} & \cdots & x_{n}^{n-1}
\end{bmatrix}\begin{bmatrix}a_{0}\\ a_{1}\\ \vdots\\ a_{n-1}\end{bmatrix}=\begin{bmatrix}y_{1}\\ y_{2}\\ \vdots\\ y_{n}\end{bmatrix}$
matrix $\begin{bmatrix}a_{0}\\ a_{1}\\ \vdots\\ a_{n-1}\end{bmatrix}$를 구하기 위해서는
n by n matrix $\begin{bmatrix}
1 & x_{1} & x_{1}^{2} & \cdots & x_{1}^{n-1} \\
1 & x_{2} & x_{2}^{2} & \cdots & x_{2}^{n-1} \\
\vdots & & & & \\
1 & x_{n} & x_{n}^{2} & \cdots & x_{n}^{n-1}
\end{bmatrix}$의 역행렬을 구해야하므로
앞서 구했던 대로 operation cost는 $\theta (n^{3})$가 필요하며 stiffness가 크면 클수록 더 정확한 값을 구하기 어려워지므로 interpolation을 하는 것이 어렵습니다.
이렇게 computational cost issue 외에도 polynomial interpolation이 어려운 이유는 또 있습니다.
higher order polynomial일수록 polynomial을 만들면 "wandering"으로 인해 physical 현상을 잘 묘사하지 못합니다.
"wandering" 문제는 바로 다음에 다룰 Lagrange polynomial interpolation에서도 발생하는 문제이므로 Lagrange polnomial interpolation에서 마저 설명하겠습니다.
2. Lagrange Polynomial Interpolation
이 Lagrange polynomial interpolation은 모든 data point를 지나면서 smooth하게 polynomial을 구할 수 있습니다.
위에서 다룬 polynomial과 다른 점은 computational cost를 낮출 수 있다는 점입니다.
Lagrange polynomial을 구하는 과정
1) 각 point $x_{j}$에 대한 degree n의 polynomial을 정의합니다.
$L_{j}(x)=a_{j}(x-x_{0})(x-x_{1})(x-x_{2})\cdots(x-x_{j-1})(x-x_{j+1}) \cdots(x-x_{n})=\alpha_{j}\prod_{i=0, i\neq j}^{n}(x-x_{i})$
$L_{j}(x)$는 $(x-x_{j})$를 제외한 나머지 항들의 곱으로 이루어진 n차 polynomial입니다.
$L_{j}(x_{k})=0 \text{ if }k\neq j$
$L_{j}(x_{j})=\alpha_{j}\prod_{i=0, i\neq j}^{n}(x_{j}-x_{i})$
$L_{j}$ 식에서 $x=x_{j}$ 외에 다른 $x_{k}$ point를 대입하면 0이 됩니다.
$\alpha_{j}=1/\prod_{i=0, i\neq j}^{n}(x_{j}-x_{i})$으로 정의하면
$L_{j}(x_{k})=\begin{cases} 0 & \text{if }k\neq j \\ 1 & \text{if }k=j\end{cases}$
으로 정리할 수 있습니다.
따라서 우리가 원하는 모든 데이터 포인트를 지나가는 lagrange polynomial
$P(x)=\sum_{j=0}^{n} y_{i}L_{j}(x)$
polynomial of degree n의 조합이 됩니다.
예를 들어, 얻은 데이터 포인트가
$i=0,1,2,3$
$x_{i}=1,2,4,8$
$y_{i}=1,3,7,11$일 때
$P(x)=1L_{0}(x)+3L_{1}(x)+7L_{2}(x)+11L_{3}(x)$
$\text{where } L_{0}(x)=\frac{(x-x_{1})(x-x_{2})(x-x_{3})}{(x_{0}-x_{1})(x_{0}-x_{2})(x_{0}-x_{3})}$
$\left\{\begin{matrix}L_{0}(x_{0})=1\\ L_{0}(x_{1})=0\\ L_{0}(x_{2})=0\\ L_{0}(x_{3})=0\end{matrix}\right.$
다음과 같이 3차 polynomial을 구했습니다. 이 polynomial에 $x_{0},\ldots, x_{3}$까지 대입해보면 이 polynomial이 모든 데이터 포인트를 지난다는 것을 알 수 있습니다.
$P(x_{0})=L_{0}(x_{0})=1=y_{0} (\because L_{1}(x_{0})=L_{2}(x_{0})=L_{3}(x_{0})=0)$
$P(x_{1})=3L_{1}(x_{1})=3=y_{1} (\because L_{0}(x_{1})=L_{2}(x_{1})=L_{3}(x_{1})=0)$
이와 같은 방식으로 모든 점을 지난다는 것을 확인할 수 있습니다.
이 Lagrange polynomial은 역행렬 계산이 필요없다는 점에서 계산 비용이 적습니다.
하지만 계산 비용을 줄였다고 해도 Lagrange polynomial interpolation, Polynomial interpolation 둘 다 사용하지 않습니다.
앞서 언급했던 "wandering" 문제 때문입니다.
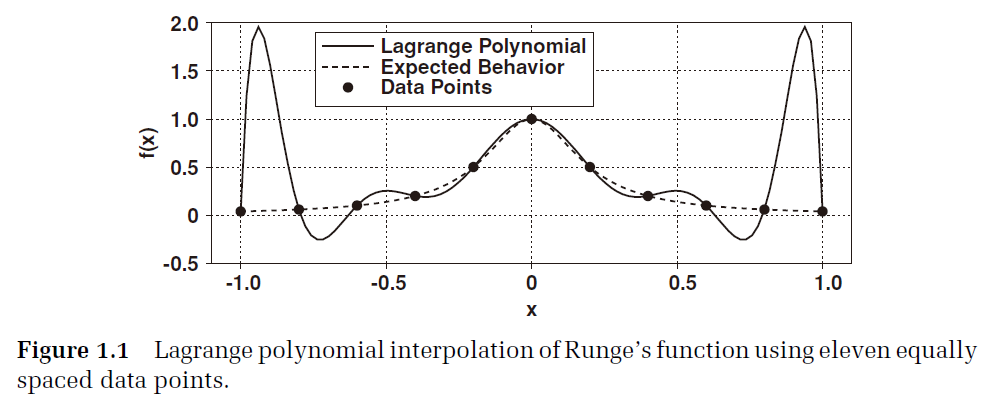
이 그림을 보시면 실선이 Lagrange Polynomial이고 점선이 예상되는 behavior입니다. n차 polynomial로 만듦으로써 실제 데이터의 경향성을 제대로 반영하지 못하는 일이 발생하고 있습니다.
이와 같은 문제 때문에 Lagrange polynomial interpolation도 부적절할 수 있습니다.
따라서 polynomial interpolation, Lagrange polynomial interpolation과 다른 방식의 interpolation을 알아보겠습니다.
다음 글로 이어집니다.
'수치해석 Numerical Analysis' 카테고리의 다른 글
| [수치해석] Numerical differentiation (1) (0) | 2021.03.19 |
|---|---|
| [수치해석] interpolation (2) - Spline interpolation (0) | 2021.03.12 |
| [수치해석] Operation cost / Condition number(Stiffness) (0) | 2021.03.04 |
| [수치해석] 수치해석 과정 예시 (0) | 2021.03.01 |
| [수치해석] Introduction (0) | 2021.03.01 |