이전 interpolation에서 이어지는 내용입니다.
1. Linear interpolation
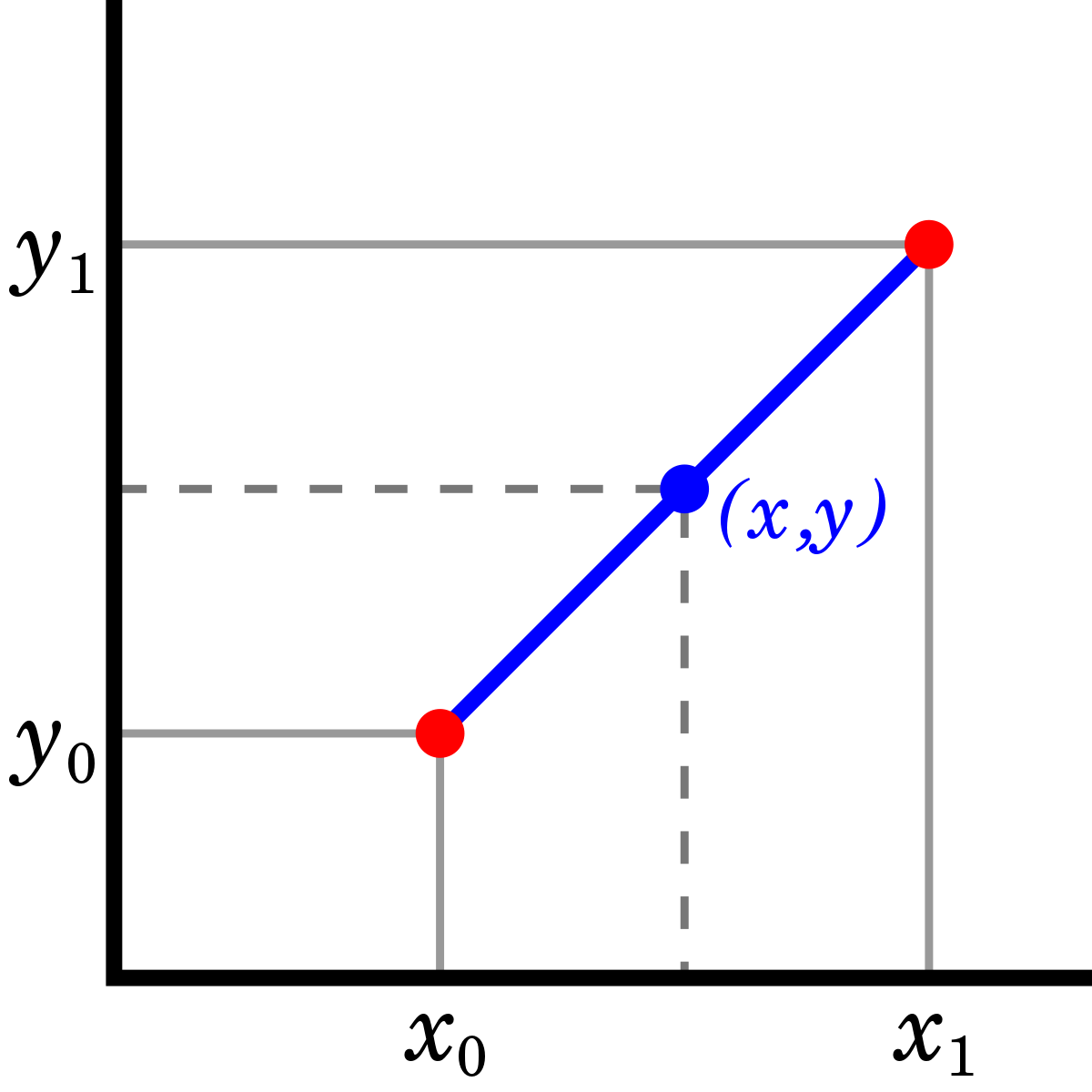
일반적으로 smooth한 것이 필요한 게 아니라면 linear interpolation을 사용해도 괜찮을 수 있습니다.
하지만 $f^{'},f^{''}, \text{ or }\int f dx$을 알고 싶은 것이 목적이기 때문에 여기서 linear interpolation은 넘어가겠습니다.
2. Cubic Spline interpolation
Spline interpolation은 공학적으로 유용한 interpolation이라고 합니다. 2차 미분도 가능하면서, computational cost도 적기 때문입니다.
예를 들어 bending 문제를 살펴보겠습니다.

외부 힘이 중력만 작용하는 경우 이 시스템을 $EIy^{''''}=G \text{ , where y is displacement}$로 모델링할 수 있습니다.
$\text{If }G=0, y^{''''}=0 \text{ between the data points}$
$y^{''''}=0 \Rightarrow y\text{ is "cubic" between } x_{i}\leq x \leq x_{i+1}$
y는 최대 3차 polynomial일 것입니다.
따라서 $\text{for ith interval}$
$F_{i}(x)=a_{0}+a_{1}x+a_{2}x^{2}+a_{3}x^{3}$
$F_{i}(x_{i})=y(x_{i})\cdots (1)$
$F_{i}(x_{i+1})=y(x_{i+1})\cdots (2)$
각 interval에 대해 3차 polynomial로 estimation한다면, i번째 interval에서 polynomial은 기존에 알고 있는 데이터 두 점을 지난다는 조건을 갖는 3차 polynomial로 식을 세웁니다. 미지수가 4개($a_{0},a_{1},a_{2},a_{3}$)이므로 조건이 2개 더 필요합니다.
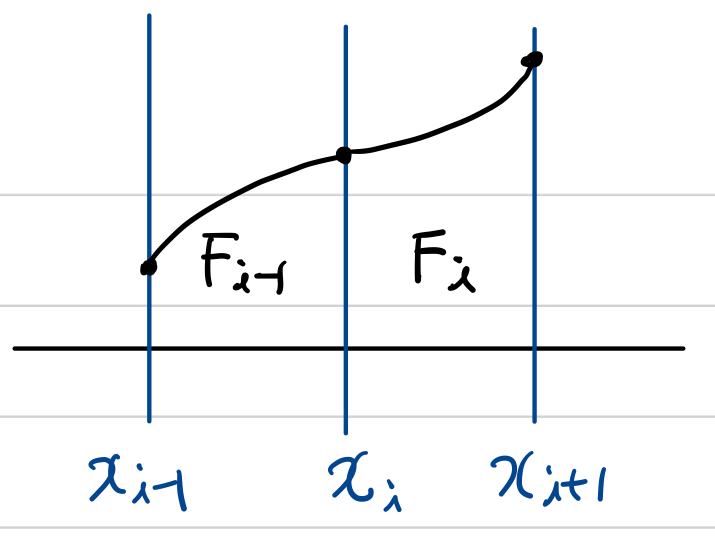
$F_{i}^{'}(x_{i})=F_{i-1}^{'}(x_{i})\cdots (3)$
$F_{i}^{''}(x_{i})=F_{i-1}^{''}(x_{i})\cdots (4)$
$x_{i}$를 기준으로 양 쪽으로 나누어진 함수 식 $F_{i-1},F_{i}$의 일차 미분, 이차 미분이 일치해야 한다는 조건을 부여함으로써 총 4개의 식과 4개의 미지수를 만들었습니다. (일치하지 않으면, 일차 미분 $f^{'}$, 이차 미분 $f^{''}$은 존재하지 않습니다.)
이 조건을 통해 $F_{i}$를 구해보도록 하겠습니다.
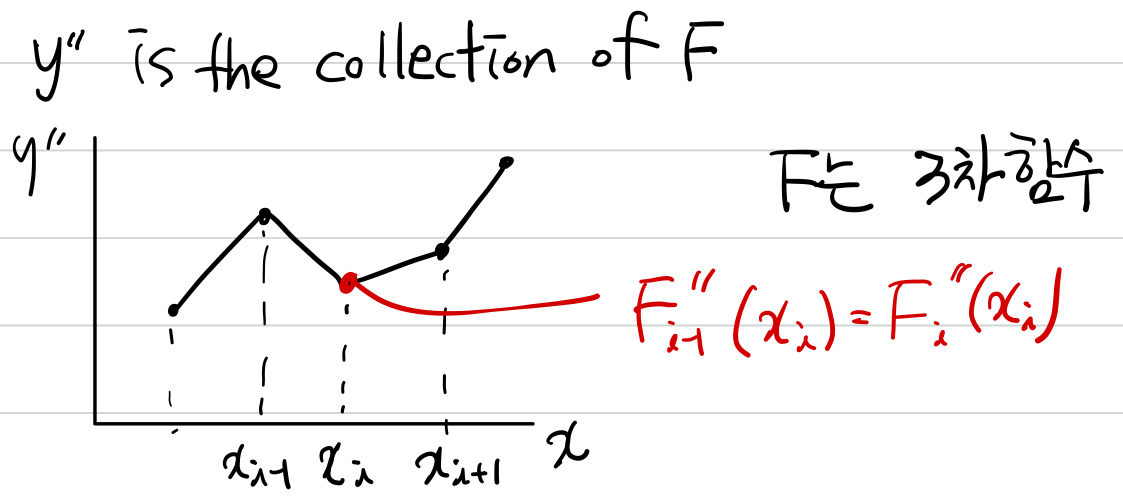
일단 (4)번 식 조건에서 시작합니다.
(4)번 식에 따르면 $F_{i-1}^{''}(x_{i})=F_{i}^{''}(x_{i})$입니다.
($F_{i}(x)$는 각 interval에서 estimate한 값이고, $g(x)$는 interpolation으로 얻은 최종적인 함수)
$\text{for }x_{i}\leq x \leq x_{i+1}$
$F_{i}^{''}(x)=g^{''}(x_{i})\frac{x-x_{i+1}}{x_{i}-x_{i+1}}+g^{''}(x_{i+1})\frac{x-x_{i}}{x_{i+1}-x_{i}}$
이 식은 $x_{i},x_{i+1}$ 사이에 있는 x에 대하여 $F^{''}$값을 구하기 위해, 직선($g^{''}$)의 내분점으로 구하듯이 값을 구한 것입니다. 이미 $F$가 3차 함수로 정했으므로, $F^{''}$는 일차함수가 되기 때문입니다.
위 식을 적분하면 $F_{i}^{'}(x)$을 구할 수 있고, 적분상수 $c_{1}$이 미지수로 남습니다.
$F_{i}^{'}(x)$를 적분하면 $F_{i}(x)$을 구할 수 있고, 적분상수 $c_{1},c_{2}$가 미지수로 남습니다.
이렇게 나온 적분상수 $c_{1},c_{2}$는 $F_{i}(x_{i})=y(x_{i}) \text{ (1) }, F_{i}(x_{i+1})=y(x_{i+1})\text{ (2)}$을 대입해서 알아낼 수 있습니다.
(자세한 풀이과정은 맨 밑에 첨부합니다.)
식 (1),(2)를 이용해서 적분상수를 구한 다음에 대입하여 얻은 식은 다음과 같습니다.
$F_{i}(x)=$
$\frac{1}{6}g^{''}(x_{i})\left [ \frac{(x_{i+1}-x)^{3}}{\Delta x_{i}}-\Delta x_{i} (x_{i+1}-x) \right ]+\frac{1}{6}g^{''}(x_{i+1})\left [ \frac{(x-x_{i})^{3}}{\Delta x_{i}}-\Delta x_{i}(x-x_{i})\right ]+y(x_{i})\frac{x_{i+1}-x}{\Delta x_{i}}+y(x_{i+1})\frac{x-x_{i}}{\Delta x_{i}}$
$\text{, where }\Delta x=x_{i+1}-x_{i}$
그런데 여기서 문제는 $g^{''}(x_{i}), g^{''}(x_{i+1})$를 모른다는 것입니다. 위 $F^{''}(x)$ 그림에서도 양 쪽의 이차 미분한 함수의 값이 같기만 하면 되기 때문에 어떤 값을 갖는지에 대한 정보는 없기 때문입니다.
그래서 마지막 조건으로 (3)번 식을 사용합니다. ((1),(2),(4) 조건은 이미 사용)
(3)번 식에 따르면 $F_{i}^{'}(x_{i})=F_{i-1}^{'}(x_{i})$입니다.
(3)번 식을 조건으로 사용하여 식을 정리하면 (자세한 과정은 이 글의 아래에 첨부)
$\frac{\Delta x_{i-1}}{6}g^{''}(x_{i-1})+\frac{\Delta x_{i-1}+\Delta x_{i}}{3}g^{''}(x_{i})+\frac{\Delta x_{i}}{6}g^{''}(x_{i+1})=\frac{y(x_{i+1})-y(x_{i})}{\Delta x_{i}}-\frac{y(x_{i})-y(x_{i-1})}{\Delta x_{i-1}}$
이제 $i=1,\ldots, n-1$을 위 식에 대입하면
$\left\{\begin{matrix}\alpha_{1} g^{''}(x_{0})+\beta_{1}g^{''}(x_{1})+\gamma_{1}g^{''}(x_{2})=R_{1}\\ \alpha_{2} g^{''}(x_{1})+\beta_{2}g^{''}(x_{2})+\gamma_{2}g^{''}(x_{3})=R_{2}\\ \vdots\\ \alpha_{n-1} g^{''}(x_{n-2})+\beta_{n-1}g^{''}(x_{n-1})+\gamma_{n-1}g^{''}(x_{n})=R_{n-1}\end{matrix}\right.$
$\begin{bmatrix}\beta_{1} & \gamma_{1} & & \cdots & 0\\ \alpha_{2} & \beta_{2} & \gamma_{2} & \cdots & 0\\ \vdots & & & & \\ 0 & & & \beta_{n-1} & \gamma_{n-1}\end{bmatrix}_{(n-1)\times(n-1)}\begin{bmatrix}g^{''}(x_{1})\\ g^{''}(x_{2})\\ \vdots\\ g^{''}(x_{n-1})\end{bmatrix}=\begin{bmatrix}R_{1}-\alpha_{1}g^{''}(x_{0})\\ R_{2}\\ \vdots\\ R_{n-1}-\gamma_{n-1}g^{''}(x_{n})\end{bmatrix}$
$\begin{bmatrix}g^{''}(x_{1})\\ g^{''}(x_{2})\\ \vdots\\ g^{''}(x_{n-1})\end{bmatrix}$를 구하기 위해서는 (n-1) by (n-1) matrix의 역행렬을 구해야 합니다.
다만 sparse matrix와 달리 Tridiagonal matrix이므로 operational cost는 $\theta (n^{1})$으로 매우 적습니다.
따라서 cubic spline interpolation은 계산 상에 이점이 있으며, smooth curve를 얻을 수 있습니다.
그런데 우변에 있는
$\begin{bmatrix}
R_{1}-\alpha_{1}g^{''}(x_{0})\\
R_{2}\\
\vdots\\
R_{n-1}-\gamma_{n-1}g^{''}(x_{n})
\end{bmatrix}$에서 경계 조건으로 사용되는 $g^{''}(x_{0})$와 $g^{''}(x_{n})$은 어떻게 알 수 있을까요?
이 값들은 맨 처음과 맨 끝 값이기 때문에 딱히 값을 추정할 방법이 없습니다.
그래서 이를 채워주기 위해 2가지 방법이 있습니다.
1) Parabolic runout (Neumann condition)
$\left\{\begin{matrix}
g^{''}(x_{0})=g^{''}(x_{1})\\
g^{''}(x_{n})=g^{''}(x_{n-1})
\end{matrix}\right.$
바로 옆에 있는 값을 그대로 가져다쓰는 방법입니다.
2) Natural spline (Dirichlet condition)
$\left\{\begin{matrix}
g^{''}(x_{0})=0\\
g^{''}(x_{n})=0
\end{matrix}\right.$
다른 값을 가져다쓰기 보다는 0으로 집어넣음으로써 해결하는 방법입니다.
wandering이 심하면 natural spline이 더 적합합니다. (수학적으로 증명이 되어있다고 합니다.)
꼭 0이 아니더라도, 시스템 상으로 경계 값을 알고 있다면 그 값을 써도 됩니다.
3. Tension spline interpolation
지금까지 배운 것은 "Cubic" spline interpolation인데 Tension spline interpolation도 있습니다.
cubic spline interpolation이 너무 구불거릴 경우(변동이 큰 경우)에 직선으로 interpolation하는(구불거림이 전혀 없는) linear interpolation을 섞어서 구불거림을 완화할 수 있습니다.
이러한 방법을 Tension spline이라 하고 cubic spline과 linear interpolation을 섞은 것으로 볼 수 있습니다.
$g_{i}^{''}(x)=g^{''}(x_{i})\frac{x-x_{i+1}}{x_{i}-x_{i+1}}+g^{''}(x_{i+1})\frac{x-x_{i}}{x_{i+1}-x_{i}}$
$g_{i}(x)=y_{i}\frac{x-x_{i+1}}{x_{i}-x_{i+1}}+y_{i+1}\frac{x-x_{i}}{x_{i+1}-x_{i}}$
이 두 식을 mixing해서
$g_{i}^{''}(x)-\sigma g_{i}(x)=\left (g^{''}(x_{i})-\sigma g_{i}(x)\right )\frac{x-x_{i+1}}{x_{i}-x_{i+1}}+\left (g^{''}(x_{i+1})-\sigma g_{i+1}(x)\right ) \frac{x-x_{i}}{x_{i+1}-x_{i}}$
$\sigma$는 linear interpolation에 대한 가중치입니다.
생략된 계산 과정


interpolation은 여기까지 하고 다음에는 Numerical differentiation을 다루겠습니다.
'수치해석 Numerical Analysis' 카테고리의 다른 글
| [수치해석] Numerical differentiation (2) (0) | 2021.03.27 |
|---|---|
| [수치해석] Numerical differentiation (1) (0) | 2021.03.19 |
| [수치해석] Interpolation (1) - Polynomial interpolation (0) | 2021.03.12 |
| [수치해석] Operation cost / Condition number(Stiffness) (0) | 2021.03.04 |
| [수치해석] 수치해석 과정 예시 (0) | 2021.03.01 |