interpolation, differentiation에 이어서 integration을 수치해석적으로 수행해보겠습니다.
1. Introduction
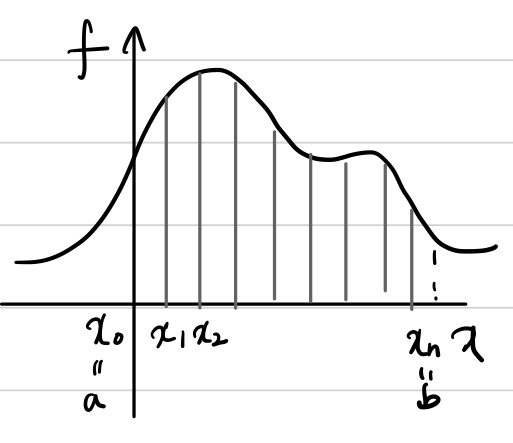
$x_{0}(=a)$부터 $x_{n}(=b)$까지 적분을 하려고 합니다.
우리는 discrete하게밖에 계산할 수 없으므로,
$I=\int_{a}^{b}f(x)dx=\sum_{j=0}^{n}f_{j}\cdot \omega_{j}$
적분을 오른쪽 식처럼 계산해야합니다. 이 때 $\omega_{j}$는 weighting factor라고 부릅니다.
이 전에 Lagrange polynomial을 배웠고, 그 polynomial 식은 $p(x)=\sum_{j=0}^{n}f_{j}L_{j}(x)$입니다.
이 방법을 통해 내가 알고 있는 데이터 점들을 충족하는 함수 식을 구할 수 있습니다.
Lagrange polynomial로 적분을 수행한다면
$I=\int_{a}^{b}p(x)dx=\int_{a}^{b}\sum_{j=0}^{n}f_{j}L_{j}(x)dx=\sum_{j=0}^{n}f_{j}\int_{a}^{b}L_{j}(x)dx$
여기서 $\int_{a}^{b}L_{j}(x)dx$이 weighting factor처럼 작용합니다.
Cotes number를 도입하겠습니다.
$\text{Cotes number : }C_{j}^{n}=\frac{1}{b-a}\int_{a}^{b}L_{j}(x)dx$
$\text{Newton-Cotes formula : }I=(b-a)\sum_{j=0}^{n}f_{j}C_{j}^{n}(x)$
후에 배울 numerical integration method는 Newton-Cotes formula의 variation입니다.
예를 들면,
$\text{if }f=1 \text{ then }\sum_{j=0}^{n}C_{j}^{n}=1$
$n=1$이라고 할 때 $x_{0}=a, x_{1}=b$입니다.
$L_{0}(x)=\frac{x-b}{a-b}$, $L_{1}(x)=\frac{x-a}{b-a}$
$C_{0}^{1}=\frac{1}{b-a}\int_{a}^{b}\frac{x-b}{a-b} dx=\frac{1}{2}$
$C_{1}^{1}=\frac{1}{b-a}\int_{a}^{b}\frac{x-a}{b-a} dx=\frac{1}{2}$

$I=(b-a)\left[ f_{0}C_{0}^{1}+f_{1}C_{1}^{1}\right]=\frac{b-a}{2}[f_{0}+f_{1}]$
이 방법은 후에 배울 Trapezoidal method에 대한 식입니다. 이에 대한 order of accuracy $\theta (h^{2})$

$n=2$인 경우에 대해서 똑같이 수행하면 $\int_{a}^{b}f(x)dx=\frac{(b-a)}{6}\left [ f(a)+4f \right( \frac{a+b}{2}\left)+f(b) \right]$
이 방법은 simpson's rule이라고 합니다. $~\theta (h^{3})$
이 때, n이 늘린다고 해서 항상 좋은 것은 아닙니다.
2. Rectangular (mid point) rule
Numerical integration 방법 중 하나인 mid point rule에 대해서 설명하겠습니다.

mid point rule은 이름에서 알 수 있는 것처럼 두 점 사이를 적분하고자 할 때 중앙값을 사용하는 방법입니다.
$\int_{x_{i}}^{x_{i+1}}f(x)dx \cong h_{i}f(y_{i})+\theta(h_{i}^{p}) \cdots (*)$
$h_{i}=x_{i+1}-x_{i}$
Taylor series expansion을 이용해서 $f(x)$를 $y_{i}$에 대해서 표현하겠습니다.
$f(x)=f(y_{i})+(x-y_{i})f^{'}(y_{i})+\frac{(x-y_{i})^{2}}{2!}f^{''}(y_{i})+\frac{(x-y_{i})^{3}}{3!}f^{'''}(y_{i})+\cdots$
이 식을 $(*)$ 좌변에 있는 $f(x)$에 대입한 다음에 적분을 수행합니다.
그 결과,
$f(y_{i})h_{i}+\left. \frac{1}{2}(x-y_{i})^{2}f^{'}(y_{i})\right |_{x_{i}}^{x_{i+1}}+\left. \frac{1}{3}\frac{(x-y_{i})^{3}}{2!}f^{''}(y_{i})\right |_{x_{i}}^{x_{i+1}}+\cdots$
$(x-y_{i})^{2}$ 등의 짝수 제곱 항은 0이 되고 홀수 번째 항만 살아남습니다.
$\int_{x_{i}}^{x_{i+1}}f(x)dx \cong h_{i}f(y_{i})+\theta(h_{i}^{p})=h_{i}f(y_{i})+\frac{1}{24}h_{i}^{3}f^{'''}(y_{i})+\theta(h_{i}^{5})$
$\left. \frac{1}{2}(x-y_{i})^{2}f^{'}(y_{i})\right|_{x_{i}}^{x_{i+1}}=0$ 등 짝수 항은 0이 됩니다.
따라서 위 식에서 가장 큰 error term은 $\frac{1}{24}h_{i}^{3}f^{''}(y_{i})$이므로, Leading order of error는 3rd order가 됩니다.
3. Trapezoidal rule
trapezoidal은 사다리꼴이라는 뜻입니다.
실제로도 이 적분 방법은 두 점 사이 적분을 사다리꼴 계산으로 수행합니다.

$\int_{x_{i}}^{x_{i+1}}f(x)dx \cong h_{i}\frac{1}{2}\left [ f(x_{i})+f(x_{i+1}) \right] \cdots (*)$
이 trapezoidal rule과 mid point rule의 오차를 비교해보고 싶기 때문에 $f(x_{i}),f(x_{i+1})$를 mid point인 $y_{i}$에 taylor series expansion으로 표현합니다.
$f(x_{i})=f(y_{i})-\frac{h_{i}}{2}f^{'}(y_{i})+\frac{h_{i}^{2}}{8}f^{''}(y_{i})-\frac{h_{i}^{3}}{48}f^{'''}(y_{i})+\cdots$
$f(x_{i+1})=f(y_{i})+\frac{h_{i}}{2}f^{'}(y_{i})+\frac{h_{i}^{2}}{8}f^{''}(y_{i})+\frac{h_{i}^{3}}{48}f^{'''}(y_{i})+\cdots$
이 두 식을 $(*)$에 대입하면,
$\frac{h_{i}}{2}\left [f(x_{i})+f(x_{i+1}) \right]=\frac{h_{i}}{2}\left(2f(y_{i})+\frac{h_{i}^{2}}{4}f^{''}(y_{i})+\cdots \right )$
$=h_{i}f(y_{i})+\frac{h_{i}^{3}}{8}f^{''}(y_{i})+\cdots$
여기서도 짝수항은 부호가 다르기 때문에 더하면 사라집니다.
위에서 mid point rule일 때
$\int_{x_{i}}^{x_{i+1}}f(x)dx = h_{i}f(y_{i})+\frac{1}{24}h_{i}^{3}f^{'''}(y_{i})+\theta(h_{i}^{5})$라는 것을 알고 있습니다.
trapezoidal에서는
$h_{i}f(y_{i})=\frac{h_{i}}{2}\left [f(x_{i})+f(x_{i+1}) \right]-\frac{h_{i}^{3}}{8}f^{''}(y_{i})+\cdots$
이기 때문에 mid point rule 식에 대입합니다.
$\int_{x_{i}}^{x_{i+1}}f(x)dx =\frac{h_{i}}{2}\left [f(x_{i})+f(x_{i+1}) \right]-\frac{1}{8}h_{i}^{3}f^{''}(y_{i}) +\frac{1}{24}h_{i}^{3}f^{''}(y_{i})+\theta(h_{i}^{5})$
error term을 보면 $-\frac{1}{12}h_{i}^{3}f^{''}(y_{i})$가 LOE입니다.
locally 3rd order의 order of accuracy를 가집니다.
따라서 trapezoidal 방법은 mid point rule과 같은 order를 가지지만 크기는 mid point rule이 더 작고($\frac{1}{24}<\frac{1}{12}$), 부호가 반대입니다.
크기가 mid point rule이 더 작기 때문에 좋아보이지만 실제로 계산을 할 때는, mid point에 대한 정보가 없기 때문에 $x_{i},x_{i+1},x_{i+2}$ 이렇게 3개의 데이터로 $x_{i+1}$을 mid point로 쓰기 때문에 각 데이터 포인트 간의 간격이 $h_{i}$에서 $2h_{i}$로 증가하고, 따라서 error는 mid point가 더 커지게 됩니다.
4. Global accuracy
위에서 trapezoidal rule의 accuracy가 locally 3rd order라고 말했는데, 왜 locally라고 언급했는지 설명하겠습니다.
[a,b] 구간의 적분을 구할 때 전체 구간이 적분을 쪼개서 적분할 수도 있습니다.
$I=\int_{a}^{b}f(x)dx=\int_{x_{0}}^{x_{1}}f(x)dx+\int_{x_{1}}^{x_{2}}f(x)dx+\cdots+\int_{x_{n-1}}^{x_{n}}f(x)dx$
만약 각 적분에 대해 trapezoidal rule을 적용한다면
$\frac{h}{2}\left [ f(x_{0})+f(x_{1})+f(x_{1})+\cdots +f(x_{n-1})+f(x_{n}) \right ]$
$=\frac{h}{2}\left [ f(a)+2\sum_{j=1}^{n-1}f(x_{j})+f(b) \right ]-\frac{1}{12}h^{3}\sum_{i=0}^{n}f^{''}(y_{i})$
전체 적분의 오차를 알아내려면 $-\frac{1}{12}h^{3}\sum_{i=0}^{n}f^{''}(y_{i})$를 구해야합니다.
# Mean value theorem
$\frac{\sum_{i=0}^{n}f^{''}(y_{i})}{n}=f^{''}(\overline{x})$ $(a\leq x\leq b)\text{ and }n=\frac{b-a}{h}$
이 Mean value theorem
$\text{L.O.E=}-\frac{h^{3}}{12}\frac{(b-a)}{h}f^{''}(\overline{x})\sim \theta(h^{2})$
하나의 panel 적분은 3rd order error이었지만
전체 panel 적분은 mean value theorem으로 2nd order error가 됩니다.
이전에 differentiation에서는 order of error는 error가 줄어드는 속도라고 언급했지만
여기서 error는 order 자체가 곧 error를 의미합니다.
5. Trapzoidal rule with end correction
이번에는 Trapzoidal rule에서 order를 높일 수 있는 방법에 대해서 알아보겠습니다.
$\int_{x_{i}}^{x_{i+1}}f(x)dx = h_{i}(f(x_{i})+f(x_{i+1}))-\frac{1}{12}h_{i}^{3}f^{''}(y_{i})+\theta(h_{i}^{5})$
이 식이 위에서 구한 Trapzoidal rule인데요,
$f^{''}(y_{i})=\frac{f^{'}(x_{i+1})-f^{'}(x_{i})}{h_{i}}+\theta(h_{i}^{2})$ 이라는 것을 numerical differentiation에서 알고 있습니다. 이 식을 위의 식에 대입하겠습니다.
$\int_{x_{i}}^{x_{i+1}}f(x)dx=\frac{h_{i}}{2}(f(x_{i})+f(x_{i+1}))-\frac{h_{i}^{2}}{12}(f^{'}(x_{i+1})-f^{'}(x_{i})+\theta(h_{i}^{5}))$
$I=\int_{a}^{b}f(x)dx=\frac{h_{i}}{2}\left [ f(a)+2\sum_{j=1}^{n-1} f(x_{j})+f(b) \right ]-\frac{h_{i}^{2}}{12}\left [ -f^{'}(x_{i})+f^{'}(x_{i+1})-f^{'}(x_{i+1})+\cdots \right ]+\sum_{i}^{n-1}\theta(h^{5})$
$=\frac{h}{2}\left [ f(a)-2\sum_{j=1}^{n-1} f(x_{j})+f(b) \right ]-\frac{h^{2}}{12}\left [ f^{'}(b)-f^{'}(a)\right ]+\theta(h^{4})$
맨 마지막에 있는 error term은 위의 4번 챕터에서 한 것처럼 mean value theorem에 의해서 차수가 하나 내려간 것입니다. 이제 저 식에서 모르는 것은 $f^{'}(b), f^{'}(a)$인데 이 경계값은 finite differentiation을 통해서 구할 수 있습니다.
2nd order error로 경계 미분값을 구하면 $\theta(h^{2})$이고 (2nd order forward, backward difference 이용)
$\frac{h^{2}}{12} \left [ f^{'}(b)-f^{'}(a) \right ]$에서 앞에 $h^{2}$이 곱해져있으므로 미분값에 대한 error는 $~\theta(h^{4})$가 됩니다.
따라서 적분값($I$)의 order of error는 $\theta(h^{4})$이고, trapezoidal rule의 LOE(Leading order of error)가 locally 3rd order이고 globally 2nd order인 것에 비해 더 개선되었습니다.
이와 같이 다른 finite difference 기법을 이용해서 error를 개선할 수 있습니다.
이제 이후에는 simpson's rule 등에 대해서 다루겠습니다.
'수치해석 Numerical Analysis' 카테고리의 다른 글
| [수치해석] Numerical integration (2) - Simpson's rule, Romberg integration, Adaptive quadrature (0) | 2021.04.04 |
|---|---|
| [수치해석/MATLAB] Lagrangian polynomial 구현하는 코드 (0) | 2021.04.02 |
| [수치해석] Error characteristics/Modified wave number (0) | 2021.03.27 |
| [수치해석] Numerical differentiation (2) (0) | 2021.03.27 |
| [수치해석] Numerical differentiation (1) (0) | 2021.03.19 |