수치해석 수업을 들으면서 수치해석으로 문제를 푸는 과정을 거치고 있습니다. (수치해석 정리글은 나중에 한꺼번에 올라갈 예정)
수치적으로 interpolation을 하는 것 중에 사용되지는 않지만 구현하기는 쉬운 Lagrangian polynomial에 대해 구현한 것을 공유하고자 합니다.
Lagranian polynomial을 만드는 방법에 대한 설명은
normal-engineer.tistory.com/95
[수치해석] Interpolation (1) - Polynomial interpolation
이번에는 수치해석에서 사용하는 interpolation 방법에 대해서 알아봅니다. 우리의 목적은 주어진 discrete data $(x_{i},y_{i})\text{ for }i=1,2,3,\ldots, n$가 있을 때 두 데이터 points 사이에 있는 point의..
normal-engineer.tistory.com
위 링크에 자세히 나와있습니다. 여기서는 코드 설명만 하도록 하겠습니다.
위의 글을 다 읽기 귀찮으신 분들을 위해서, 중요한 부분만 캡쳐했습니다.
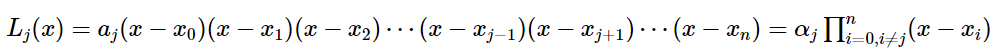

$y_{i}$는 데이터 샘플에서 주어진 y값이고 $L_{j}(x)$를 모두 구해서 lagrange polynomial인 $P(x)$를 구하는 게 목표입니다.
저의 경우에는 LagrangePolynomial이라는 함수를 만들어서 사용했습니다.
MATLAB에서 함수를 사용하는 방법은 함수명을 사용하는 코드를 만든 다음에 내가 함수를 가져와서 쓸 코드를 함수 코드와 같은 경로에 넣어두는 것입니다. 아래의 코드는 LagrangePolynomial.m으로 저장하고, 같은 폴더의 example.m 코드 있다면 example.m 코드에서 LagrangePolynomial(x,y)와 같은 방식으로 사용 가능합니다.
굳이 함수로 사용하지 않더라도 아래 코드 자체로도 수행할 수 있습니다.
코드 구성 : 변수 선언 - $a(n)$ 구하기 - $L_{j}$ 구하기 - $P(x)$ 구하기
function [P,L] = LagrangePolynomial(x_s, y_s)
x = sym('x');
len = length(x_s);
L = sym(ones(len,1));
a = ones(len,1);
for n = 1:len
multi = 1;
% Calculate alpha term
for m = 1:len
if m ~= n
multi = multi * (x_s(n)-x_s(m));
end
a(n)= 1/multi;
end
% Find L_{i}
L(n)=a(n);
for k = 1:len
if k ~= n
L(n)= L(n)*(x - x_s(k));
end
end
end
P = 0;
% Lagrange Polynomial
for i = 1:len
P = P + y_s(i)*L(i);
end처음에는 변수를 할당합니다. x라는 심볼릭을 사용할 거고, 주어진 sample data의 갯수를 변수 len에 넣습니다.
Laplace function($L_{j}$)을 j에 대해서 각각 넣기 위해 L이라는 변수를 심볼릭 matrix로 만듭니다.
심볼릭으로 행렬을 만들어주지 않으면 에러가 발생하니 주의하시기 바랍니다.
for 문에서는 $a(n)$을 구하는 과정이 내부의 첫번째 for문으로 들어가있습니다. (주석 %Calculate alpha term 부분)
그 다음에는 $L_{i}$를 구할 수 있도록 L matrix에 각 원소를 집어넣었습니다.
마지막으로 $P(x)$는 $L_{j}$의 조합으로 들어가있으므로 다 더해주면 됩니다.
'수치해석 Numerical Analysis' 카테고리의 다른 글
| [수치해석] Numerical integration (3) - Gauss quadrature (0) | 2021.04.04 |
|---|---|
| [수치해석] Numerical integration (2) - Simpson's rule, Romberg integration, Adaptive quadrature (0) | 2021.04.04 |
| [수치해석] Numerical integration (1) - Mid point rule, Trapezoidal rule (0) | 2021.03.28 |
| [수치해석] Error characteristics/Modified wave number (0) | 2021.03.27 |
| [수치해석] Numerical differentiation (2) (0) | 2021.03.27 |