1. General procedure to obtain first difference derivatives
이전에 한 논의에 이어서, taylor table을 만드는 과정에 대해서 알아보고자 합니다.
일단 한 예시를 보고 그것을 확장할 수 있습니다.
ex) $f_{j}^{'}$를 $f_{j},f_{j+1},f_{j+2}$를 이용해 구하고자 합니다.
최종적으로 $f_{j}^{'}+a_{0}f_{j}+a_{1}f_{j+1}+a_{2}f_{j+2}=\theta(h^{p})\text{, where }h=\Delta x=x_{j+1}-x_{j}=x_{j+2}-x_{j+1}$
의 형태로 나타냄으로써 $f_{j}^{'}$를 $f_{j},f_{j+1},f_{j+2}$에 대해서 표현하고, 그 때 발생하는 오차의 maximum order of accuracy는 p입니다.
이렇게 만들려면 이전 글에서 작성했던 것처럼 taylor expansion으로 $f_{j},f_{j+1},f_{j+2}$를 $f_{j}$의 미분에 대해서 표현해야합니다.
아래 그림은 이를 정리한 것입니다.

위 그림의 첫번째 행은 $f_{j}$부터 일차미분, 이차미분... 차수를 늘려가면서 미분한 것입니다.
그리고 첫번째 열은 $f_{j}^{'}, a_{0}f_{j}, a_{1}f_{j+1}, a_{2}f_{j+2}$이고 이 각각의 값에 대해 taylor expansion한 결과가 두번째 열부터 나와있습니다.
두번째 행부터 마지막 행까지 더하면
$f_{j}^{'}+a_{0}f_{j}+a_{1}f_{j+1}+a_{2}f_{j+2}=$
$(a_{0}+a_{1}+a_{2})f_{j}+(1+a_{1}h+2a_{2}h)f_{j}^{'}+\left ( a_{1} \frac{h^{2}}{2!}+a_{2} \frac{ (2h)^{2} }{ 2! } \right ) f_{j}^{''}+\left ( a_{1}\frac{h^{3}}{3!}+a_{2}\frac{(2h)^{3}}{3!}\right ) f_{j}^{'''}+\cdots (*)$
우리는 이 식의 우변에서 order가 maximum으로 만들게 하고 싶기 때문에
$a_{0}+a_{1}+a_{2}=0$
$1+a_{1}h+2a_{2}h=0$
$a_{1}\frac{h^{2}}{2!}+a_{2}\frac{(2h)^{2}}{2!}=0$
으로 설정하겠습니다. 이 세 개의 식을 연립방정식으로 풀면 위 식을 만족하는 $a_{0},a_{1},a_{2}$를 구할 수 있습니다.
식을 세 개로 잡은 이유는 위 식에서 미지수가 3개이기 때문에 최대 3개의 식을 사용할 수 있기 때문입니다.
이렇게 하면 $(*)$식을 다음과 같이 만들 수 있습니다.
$f_{j}^{'}+a_{0}f_{j}+a_{1}f_{j+1}+a_{2}f_{j+2}=(a_{1}\frac{h^{3}}{3!}+a_{2}\frac{(2h)^{3}}{3!})f_{j}^{'''}+\cdots$
참고로 위 연립방정식을 풀면 $a_{0}=\frac{3}{2h}, a_{1}=-\frac{2}{h},a_{2}=\frac{1}{2h}$가 나옵니다.
$a_{0},a_{1},a_{2}$를 알기 때문에 $(a_{1}\frac{h^{3}}{3!}+a_{2}\frac{(2h)^{3}}{3!})\neq 0$인 것도 알 수 있습니다.
$f_{j}^{'}=-a_{0}f_{j}-a_{1}f_{j+1}-a_{2}f_{j+2}+\theta(h^{2})=\frac{-3f_{j}+4f_{j+1}-f_{j+2}}{2h}+\theta(h^{2})$
즉 $f_{j}^{'}$를 numerical differentiation으로 세 개의 forward항을 썼을 때 maximum order of accuracy는 2입니다.
따라서 이 방법은 2nd order forward finite differentiation for $f_{j}^{'}$
이와 같은 방법으로 다양한 scheme의 differentiation을 진행할 수 있습니다. (여기서 scheme은 order와 방향이 다른 finite differentiation을 말합니다.)
왜 다양한 scheme이 필요할까요?
error term의 characteristics이 달라서 problem에 따라 적절한 방법을 사용합니다.
또한 항을 늘릴수록 order가 커지니까 좋아보일 수 있지만 항을 늘릴 때 문제가 발생할 수도 있습니다.
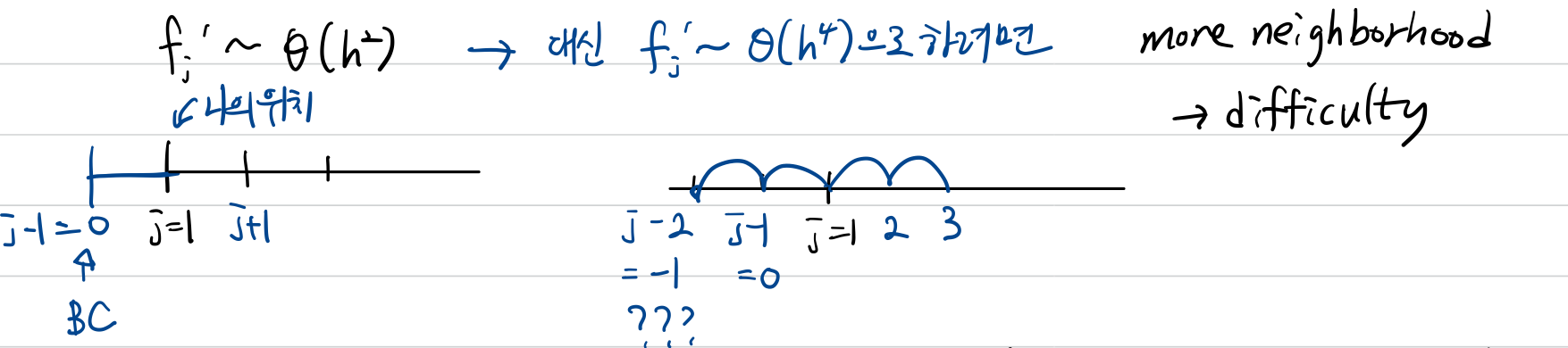
2nd order central scheme을 사용할 때는 나의 위치가 j=1일 때 j-1과 j+1을 사용하므로 boundary condition을 필요로 합니다.
4th order로 만들기 위해서는 j-2, j-1, j, j+1, j+2 까지 현재 위치를 중심으로 양 옆에 2개의 포인트가 필요합니다. 그러나 이때는 j=0, j=1에서 값을 구할 수 없는 neigborhood가 존재한다는 문제가 있기 때문에 위치가 최소 j=2가 되어야하며, 또 5개의 element로 계산을 해야하기 때문에 computational cost가 늘어난다는 문제가 있습니다.
2. Pade scheme
이 문제를 해결하기 위해 Pade approximation을 사용할 수 있습니다.
계산비용도 적고, 현재 위치를 기준으로 양 옆에 있는 neigborhood만 사용합니다.
neigborhood의 derivative를 사용함으로써 효율을 높이고, order도 줄일 수 있습니다.
$f_{j+1},f_{j-1},f_{j},f_{j+1}^{'},f_{j-1}^{'}$를 사용해서 $f_{j}^{'}$를 구하는 것이 목표입니다.
$f_{j}^{'}+b_{1}f_{j+1}^{'}+b_{-1}f_{j-1}^{'}+a_{1}f_{j+1}+a_{0}f_{j}+a_{-1}f_{j-1}=\theta$

다음 그림에서 미지수는 5개($a_{0},a_{1},a_{-1},b_{1},b_{-1}$)이므로 두 번째 열부터 여섯 번째 열까지 모두 총 합이 0이 되도록 설정함으로써 order를 4로 만들 수 있습니다.
$a_{0}=0, a_{1}=-\frac{-3}{4h}, a_{-1}=\frac{3}{4h}, b_{1}=\frac{1}{4}, b_{-1}=\frac{1}{4}$
위에서 구한 것이 4th order Pade scheme입니다.
General procedure for obtaining $f_{j}$
위에서 구한 Pade scheme을 이용해서 f 전체의 derivatives를 구하려고 합니다.
$f_{j-1}^{'}+4f_{j}^{'}+f_{j+1}^{'}=-\frac{3}{h}(f_{j-1}-f_{j+1})+\theta(h^{4})$
$\left\{\begin{matrix}
j=1 & f_{0}^{'}+4f_{1}^{'}+f_{2}^{'}=-\frac{3}{h}(f_{0}-f_{2}) \\
j=2 & f_{1}^{'}+4f_{2}^{'}+f_{3}^{'}=-\frac{3}{h}(f_{1}-f_{3})\\
\vdots & \\
j=n-1 & f_{n-2}^{'}+4f_{n-1}^{'}+f_{n}^{'}=-\frac{3}{h}(f_{n-2}-f_{n})
\end{matrix}\right.$
$\begin{pmatrix}4 & 1 & & & 0 \\ 1 & 4 & 1 & & \\ 0 & 1 & 4 & 1 & \\ & & & \ddots & \\ 0 & & & & \end{pmatrix} \begin{pmatrix}f_{1}^{'}\\ f_{2}^{'}\\ \vdots \\ f_{n-1}^{'}\end{pmatrix}=-\frac{3}{h}\begin{pmatrix}RHS_{1}-f_{0}^{'}\\ RHS_{2}\\ \vdots\\ RHS_{n-1}-f_{n}^{'}\end{pmatrix}$
TDMA는 계산하는데 $\theta(n^{1})$의 operation cost가 든다. 즉, 전체 포인트에서 함수 미분값을 구하는 데 계산 cost가 매우 적게 듭니다.
함수의 미분값을 사용해서 finite differentiation을 시도했을 뿐인데 계산cost가 적으면서도 order of accuracy가 증가하는 결과를 얻을 수 있었습니다.
그런데 이 방법을 쓸 때는 $f_{0}^{'}, f_{n-1}^{'}$을 알아야 한다. 이 경우에는 $f_{0}^{'}$의 order of accuracy가 third order보다는 높아야 합니다. 따라서 맨 끝의 두 미분 값을 구할 때는 항을 4개 잡아서 finite 방법으로 구할 수 있습니다.
$f_{0}^{'}$라면 j=0, 1, 2, 3을 사용하는 forward 방식이고,
$f_{n-1}^{'}$하면 j=n, n-1, n-2, n-3을 사용하는 backward 방식입니다.
finite deferentiation은 여기까지하고 다음에는 error의 특성을 modified wave number와 연결지어서 정리하겠습니다.
'수치해석 Numerical Analysis' 카테고리의 다른 글
| [수치해석] Numerical integration (1) - Mid point rule, Trapezoidal rule (0) | 2021.03.28 |
|---|---|
| [수치해석] Error characteristics/Modified wave number (0) | 2021.03.27 |
| [수치해석] Numerical differentiation (1) (0) | 2021.03.19 |
| [수치해석] interpolation (2) - Spline interpolation (0) | 2021.03.12 |
| [수치해석] Interpolation (1) - Polynomial interpolation (0) | 2021.03.12 |