1. Introduction
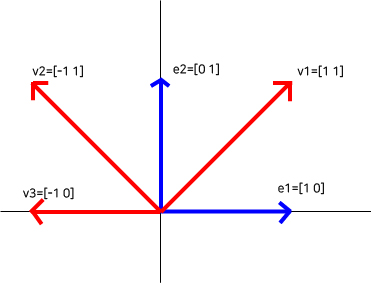
(위 그림 상에서 [0 1]은 $\begin{bmatrix}0&1\end{bmatrix}^{T}$와 같다는 것에 유의해주세요)
한 vector $\begin{bmatrix}x&y\end{bmatrix}^{T}$가 있을 때 $x\begin{bmatrix}1&0\end{bmatrix}^{T}+y\begin{bmatrix}0&1\end{bmatrix}^{T}$ 두 벡터(위 그림의 e1, e2)의 조합으로 모든 x,y에 대해 표현할 수 있습니다.
이 때 조합할 때 사용되는 계수 (x,y)로 unique하게 한 개밖에 없습니다. 예를 들어
$\begin{bmatrix}-2\\0\end{bmatrix}$를 표현하고 싶다면 $(-2)\times e1+0\times e2$ 외에 e1, e2를 조합해서 나타낼 방법이 없습니다.
만약 vector가 v1, v2, v3가 있다고 해보겠습니다.
$v1=\begin{bmatrix}1\\1\end{bmatrix}$
$v2=\begin{bmatrix}-1\\1\end{bmatrix}$
$v3=\begin{bmatrix}-1\\0\end{bmatrix}$
$\begin{bmatrix}-2\\0\end{bmatrix}$을 $v1,v2,v3$를 이용해서 표현해보겠습니다.
$\begin{bmatrix}-2\\0\end{bmatrix}=2v3=-v1+v2$
unique하게 하나의 조합으로만 표현하는 것이라 여러 방법으로 벡터를 표현할 수 있습니다.
이렇게 여러 가지 벡터들을 선형 조합하여 다른 벡터를 표현하는 이유는, 이것이 basis, linear independence 개념에 있어서 중요하기 때문입니다.
처음에 소개한 $e1, e2$는 두 벡터로 다른 모든 벡터들을 unique하게 표현할 수 있으므로 basis라고 합니다. (개념은 뒤에..)
$v1,v2,v3$는 unique하게 표현할 수 없으므로 basis라고 할 수 없습니다.
2. Spanning space
$V\text{ : a vector space } v_{1},\ldots,v_{k}\in V$
$\text{Def) }<v_{1},v_{2},\ldots,v_{k}>=\{a_{1}v_{1}+a_{2}v_{2}+\cdots+a_{k}v_{k}, a_{i}\in \mathbb{R}\}$
$\text{Ex) }A=\begin{bmatrix}1&2\\2&4\\3&6\end{bmatrix}$
$C(A)=<\begin{bmatrix}1\\2\\3\end{bmatrix},\begin{bmatrix}2\\4\\6\end{bmatrix}>=<\begin{bmatrix}1\\2\\3\end{bmatrix}$
3. Linear Independence
$\text{Definition) }$
$v_{1},v_{2},\cdots,v_{n}\text{ are linearly dependent if for some i, }v_{i}=c_{1}v_{1}+c_{2}v_{2}+\cdots+c_{i}v_{i}+\cdots+c_{n}v_{n}$
$\Leftrightarrow \text{There are }c_{1},c_{2},\cdots,c_{n}\text{ with }c_{i}\neq 0\text{ for some i such that }c_{1}v_{1}+\cdots+c_{n}v_{n}=0$
$v_{1},v_{2},\cdots,v_{n}\text{ are linearly independent if}$
$c_{1}v_{1}+c_{2}v_{2}+\cdots+c_{i}v_{i}+\cdots+c_{n}v_{n}=0\text{ implies }c_{1}=0,c_{2}=0,\cdots,c_{n}=0$
만약 $c_{1}v_{1}+c_{2}v_{2}+\cdots+c_{i}v_{i}+\cdots+c_{n}v_{n}=0$일 때, $c_{i}\neq 0$이라면
$v_{i}=-\frac{c_{1}}{c_{i}}v_{1}+\cdots-\frac{c_{n}}{c_{i}}v_{n}$
다음과 같이 표현할 수 있는데 식을 해석하자면, $v_{i}$를 $v_{1},\ldots,v_{n}$으로 표현할 수 있는 것입니다. 즉, $v_{1},\ldots,v_{n}$에 dependent합니다.
예를 들어 $A=\begin{bmatrix}3 & 4 & 2\\ 0 & 1 & 5\\ 0 & 0 & 2\end{bmatrix}$와 같은 matrix가 있을 때 각 column을 vector라고 생각하겠습니다.
$v_{1}=\begin{bmatrix}3\\0\\0\end{bmatrix}$
$v_{2}=\begin{bmatrix}4\\1\\0\end{bmatrix}$
$v_{3}=\begin{bmatrix}2\\5\\2\end{bmatrix}$
$c_{1}v_{1}+c_{2}v_{2}+c_{3}v_{3}=0$
다음 식을 만족하는 $c_{1},c_{2},c_{3}$를 찾아보면 0밖에 없다는 사실을 알 수 있습니다.
이를 통해 $v_{1},v_{2},v_{3}$는 linear independent라는 사실을 알 수 있습니다.
또한 이전에 배웠던 Null space 개념과 연관지을 수 있습니다.
$\begin{bmatrix}3 & 4 & 2\\ 0 & 1 & 5\\ 0 & 0 & 2\end{bmatrix}\begin{bmatrix}c_{1}\\c_{2}\\c_{3}\end{bmatrix}=0$
다음을 만족하는 벡터를 구했을 때 영벡터 밖에 없으므로 Null space에 영벡터 밖에 없다고 볼 수 있습니다.
$\text{Theorem) The column vectors of A are linearly independent }\Leftrightarrow Ax=0\text{ has only one solution }x=0$
$\begin{bmatrix}v_{1}&v_{2}&\cdots&v_{n}\end{bmatrix}\begin{bmatrix}c_{1}\\ \vdots \\c_{n}\end{bmatrix}=0$
$\text{Theorem) Any n vectors }v_{1},v_{2},\ldots,v_{n}\in \mathbb{R}^{m}\text{ are linearly dependent if n>m}$
$n=4,m=3$
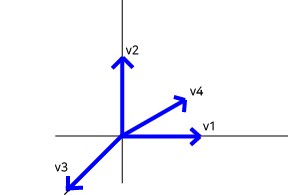
3차원의 4개의 벡터가 있을 때 3개의 벡터가 최대 linearly independent 가능하므로 한 개는 반드시 dependent할 수밖에 없다.
$v_{4}$를 $v_{1},v_{2},v_{3}$ 벡터로 표현 가능
$\text{proof) }$
$\text{want to show that there are }c_{1},c_{2},\ldots,c_{n}\text{ (not all zero) such that }c_{1}v_{1}+c_{2}v_{2}+\cdots+c_{n}v_{n}=0$
$m\left\{ \begin{matrix}\begin{bmatrix}v_{1} & v_{2} & \cdots & v_{n}\end{bmatrix}\end{matrix}\right. \begin{bmatrix}c_{1}\\ c_{2}\\ \vdots\\ c_{n}\end{bmatrix}=0$
$n>m$이면 미지수가 방정식보다 많으므로 해가 무한히 많다. 즉, linearly dependent하다.
4. Basis
$v_{1},v_{2},\ldots,v_{n}\text{ form a basis of V}$
$\text{if (1). }v_{1},\ldots,v_{n}\text{ are linearly independent}$
$\text{(2). }v_{1},\ldots,v_{n}\text{ span V}$
만약 $v_{1},v,{2},\ldots,v_{n}$이 basis라면 어떤 벡터든 $v_{1},v,{2},\ldots,v_{n}$의 Linearly combination으로 uniquely 표현할 수 있다.
$\text{proof) }$
(2)에 의해 $v=c_{1}v_{2}+\ldots+c_{n}v_{n}$
(1)에 의해 uniqueness를 증명할 수 있습니다.
$v=a_{1}v_{1}+a_{2}v_{2}+\ldots+a_{n}v_{n}=b_{1}v_{1}+b_{2}v_{2}+\ldots+b_{n}v_{n}$
$(a_{1}-b_{1})v_{1}+\ldots+(a_{n}-b_{n})v_{n}=0 \Rightarrow a_{i}=b_{i}\text{ for all i}$
$v_{1},\ldots,v_{n}$은 linearly independent이기 때문에 위 식의 각 계수는 모두 0이어야하고 따라서 $a_{i}=b_{i}$
$\text{example) }$
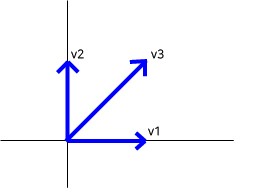
$v_{1}$ 벡터 하나만 있다고 했을 때 $v_{1}$벡터는 a basis of $\mathbb{R}^{2}$가 될 수 없다.
$v_{1},v_{2}$
$v_{2},v_{3}$
$v_{1},v_{3}$ form a basis
그러나 $v_{1},v_{2},v_{3}$은 basis를 형성할 수 없다. not linearly independent이기 때문입니다.
dimension of a vector space V는 basis의 elements 갯수와 같습니다.
3차원에 속한 어떤 vector space V를 span하기 위해 존재해야만 하는 벡터는 3개입니다.
5. Linear independence, basis, dimension과의 관계
$\text{Let V be a vector space of dimension n}$
$\text{1) Any set of n linearly independent vectors is a basis for V}$
$\text{2) Any set of n vectors spanning V is a basis for V}$
$\text{Theorem) }$
$v_{1},v_{2},\ldots,v_{m} \text{ and } w_{1},w_{2},\ldots,w_{n} \text{ basis of V, then m=n}$
basis는 unique하지 않기 때문에 여러 경우가 존재하지만 같은 vector space의 basis에 속한 벡터의 갯수는 항상 같습니다.
$\text{proof) }$
$n>m$이라고 가정할 때 $v_{1},v_{2},\ldots,v_{m} \text{ and } w_{1},w_{2},\ldots,w_{n}$ 모두 basis라고 하겠습니다.
$\left\{\begin{matrix}
w_{1}=a_{11}v_{1}+a_{21}v_{2}+\ldots+a_{m1}v_{m}\\
w_{2}=a_{12}v_{1}+a_{22}v_{2}+\ldots+a_{m2}v_{m}\\
\vdots\\
w_{n}=a_{1n}v_{1}+a_{2m}v_{2}+\ldots+a_{mn}v_{m}
\end{matrix}\right.$
이 식을 matrix로 나타내면 다음과 같습니다.
$\begin{bmatrix}w_{1} & w_{2} & \cdots & w_{n}\end{bmatrix}=\begin{bmatrix}
v_{1} & v_{2} & \cdots & v_{m}
\end{bmatrix}\begin{bmatrix}
a_{11} & \cdots & a_{1n}\\
\vdots & & \\
a_{m1} & \cdots & a_{mn}
\end{bmatrix}$
위의 a element를 가진 matrix를 A라고 할 때
$A\begin{bmatrix}c_{1}\\ \vdots\\ c_{n}\end{bmatrix}=0\text{, where }\begin{bmatrix}c_{1}\\ \vdots\\ c_{n}\end{bmatrix}\neq 0$
$n>m$이기 때문에 미지수가 방정식보다 더 많으므로 0이 아닌 해가 존재합니다.
(방정식이 미지수보다 더 많으면 해가 없을 수도 있습니다.)
즉, $c_{1}w_{1}+\ldots+c_{n}w_{n}=0$에서 $c_{i}\neq 0$이므로 $w_{1},\ldots,w_{n}$은 linearly dependent입니다. basis 조건에 어긋나므로 모순입니다.
마찬가지로 $n<m$일 때도 $w,v$만 바꿔서 모순임을 보일 수 있습니다.
따라서 $m=n$입니다.
$\text{Let V be a vector space with dim V = k}$
$v_{1},\ldots,v_{n}\left\{\begin{matrix}
\text{ are linearly dependent if} n>k\\
\text{ do not span V if }n<k
\end{matrix}\right.$
위의 결과를 바탕으로 이렇게 정리할 수 있을 것 같습니다. vector space V의 dimension이 k일 때,
vector space에 속한 $v_{1},\ldots,v_{n}$에서 n이 k보다 크면 linearly dependent하므로 basis가 될 수 없습니다.
n이 k보다 작으면 V를 span할 수 없습니다.
그렇다고 n과 k이 같다고 무조건 basis가 되는 것은 아닙니다. 위에서 다룬 basis의 조건을 검증해봐야합니다.
즉, n=k는 basis의 필요조건이지 충분조건은 아닙니다.
이제 특정 vector space에서 matrix를 예시로 basis를 살펴보겠습니다.
$\text{ A : m by n matrix, }v_{1},\ldots,v_{n}\text{ column vectors}$
$A=\begin{bmatrix}v_{1} & v_{2} & \ldots & v_{n}\end{bmatrix}$
$v_{1},v_{2},\ldots,v_{n}$는 $\mathbb{R}^{m}$의 basis가 될 수 있을까요?
$\text{(1). m<n : Not linearly independent }\Rightarrow \text{if they span V, then by discarding some elements, one can}$
$\text{(2). n<m : does not span }\mathbb{R}^{m}\Rightarrow \text{if they are linearly independent, one can add some vectors }v_{n+1},\ldots,v_{m}$
$\text{ so that }v_{1},\ldots,v_{m}\text{ form a basis of }\mathbb{R}^{m}$
$\text{(3). n=m : }$
$v_{1},\ldots,v_{m}\text{ form a basis of }\mathbb{R}^{n}\Leftrightarrow A\text{ is invertible}$
이 경우에는 벡터들이 basis가 된다면 A는 invertible하다는 말과 동치입니다.
matrix에서 다룬 내용이 위에서 다룬 내용과 크게 차이가 없다는 생각이 들 수도 있습니다.
하지만 matrix($\mathbb{R}^{m\times n}$)를 구성하는 column vector가 basis라는 말이 A matrix의 invertible과 연관되어있다는 점은 굉장히 중요합니다.
matrix가 invertible하기 위해서는 column이 linearly independent해야한다는 것도 알 수 있습니다.
이와 같이 matrix의 성질을 다른 관점에서 생각해볼 수 있습니다.
다음에는 fundamental subspace에 대해 이야기하겠습니다.
'수학 Mathematics > 선형대수학 Linear Algebra' 카테고리의 다른 글
| [응용선형대수] Linear Transformations (0) | 2021.03.05 |
|---|---|
| [응용선형대수] The four fundamental subspaces (0) | 2021.03.04 |
| [응용선형대수] Understanding Ax=0, Ax=b using null space matrix (0) | 2021.02.25 |
| [응용선형대수] Null space/Column space (0) | 2021.02.25 |
| [선형대수] Rectangular matrix의 곱과 singularity (0) | 2021.02.22 |