뛰는 놈 위에 나는 공대생

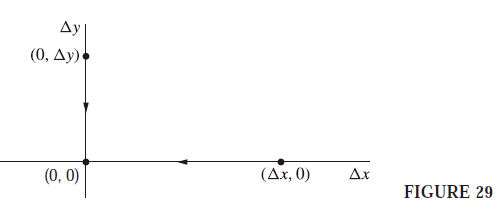
이전에 $f(z)$를 두 real-valued function $u(x,y)+iv(x,y)$으로 볼 수 있다는 것을 배웠습니다. 당연히 $f^{'}(z)$와 $u(x,y),v(x,y)$의 derivatives와도 연관성이 있을 것입니다. 만약 $f^{'}(z)$가 존재한다면, $u(x,y),v(x,y)$의 first-order partial derivatives가 만족해야만 하는 조건이 있습니다. 이를 통해 $f^{'}(z_{0})$를 $u,v$에 대해서 표현하는 방법도 알게 될 것입니다. Cauchy-Riemann equation은 그에 대한 내용입니다. $\text{first-order partial derivatives of the component functions u and v of a func..