1. Introduction
Runge Kutta 방법(이하 RK 방법)은 explicit method 중에서 nonlinear에 적합하기 때문에 많이 쓰입니다.
substep method라고 해서, RK방법은 한 타임스텝을 한 번에 계산하는 것이 아니라 여러 스텝으로 나눠서 진행하는 방법입니다.
Advantage
1) Stability가 좋다 (일반 explicit method에 비해 stability 영역이 넓음)
2) time step size를 바꿔가면서 사용할 수 있다 (이 글에서는 균일한 간격을 사용하지만 달라도 가능하다)
3) self-starting (이후에 나오는 multistep method는 초기 조건만으로 시작할 수가 없지만 이 방법은 가능)
RK방법도 2차, 3차, 4차 등 차수를 계속 높일 수가 있습니다. 여기 글에서는 2차, 4차만 다룬다는 점을 알아주세요.
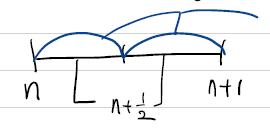
$n$스텝에서 $n+1$스텝으로 넘어갈 때 중간에 $n+\frac{1}{2}$ 스텝을 추가합니다. 중간에 한 스텝 더 추가해서 2nd order RK method(RK2로 표현)입니다.
$y^{n+\frac{1}{2}}=y^{n}+\frac{\Delta t}{2} f\left(y^{n}, t^{n}\right)$
$y^{n+1}=y^{n+\frac{1}{2}}+\frac{\Delta t}{2} f\left(y^{n+\frac{1}{2}}, t^{n+\frac{1}{2}}\right)$
각각의 식은 Explicit euler와 같습니다.
이 방법을 model problem에 적용해서 바꾸겠습니다.
$\text{model problem : }y^{\prime}=\lambda y$
$\begin{aligned} y^{n+\frac{1}{2}} &=y^{n}+\frac{\lambda \Delta t}{2} y^{n} \\ y^{n+1} &=y^{n}+\lambda \Delta t\left(y^{n+\frac{1}{2}}\right) \\ y^{n+1} &=y^{n}+\lambda \Delta t y^{n}+\frac{(\lambda \Delta t)^{2}}{2} y^{n}=\left(1+\lambda \Delta t+\frac{(\lambda \Delta t)^{2}}{2}\right) y^{n} \end{aligned}$
$y^{n}=(\sigma_{RK_{2}})^{n} y^{0} \quad \sigma_{RK_{2}}=1+\lambda \Delta t+\frac{(\lambda \Delta t)^{2}}{2}$
식을 정리해보면 Predictor-Corrector 방법과 거의 유사합니다.
2. Runge-Kutta method의 generalization
RK방법의 차수를 올리는 방법은 중간에 지나가는 step 수를 늘리는 것으로, 스텝을 늘릴수록 유도하는 것도, 계산 과정도 복잡해집니다. 위에서 언급한 2nd order 방법은 중간스텝을 한 번 추가한 것에 대한 최적의 결과입니다.
즉, 아래 그림처럼
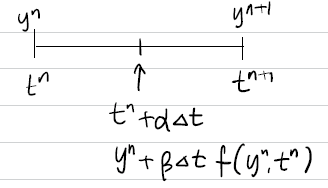
$n$스텝과 $n+1$스텝 사이에 중간 스텝을 추가할 때(2 steps) 굳이 $\frac{1}{2}\Delta t$ 간격을 갖는 것이 아니라 $\alpha \Delta t$를 정합니다.
$y^{n+1}=y^{n}+\gamma_{1} k_{1}+\gamma_{2} k_{2}$
$k_{1}=\Delta t f\left(y^{n}, t^{n}\right)$
$k_{2}=\Delta t f\left(y^{n}+\beta k_{1}, t^{n}+\alpha \Delta t\right)$
$k_{2}$ 식을 보면 $\Delta t f\left(y^{n}, t^{n}\right)$ 대신 $k_{1}$을 쓴 것을 확인할 수 있습니다.
그리고 $y^{n+1}$을 구할 때 $t^{n}$일 때와 $t^{n}+\alpha\Delta t$일 때를 가중치($\gamma_{1},\gamma_{2}$)를 곱해서 조합하여 다음 스텝(n+1)값을 구합니다.
$y^{n+1}$을 $y^{n}$일 때 값을 기준으로 taylor series expansion을 하면
$y^{n+1}=y^{n}+\Delta t y^{n^{\prime}}+\frac{\Delta t^{2}}{2 !} y^{n^{\prime \prime}}+\frac{\Delta t^{3}}{3 !} y^{n^{\prime \prime \prime}}+\cdots$
이 때,
$\left[\begin{array}{l}y^{\prime}=f(y, t) \\ y^{\prime \prime}=f_{t}+f \cdot f_{y}\end{array}\right.$
이므로 이 식을 위의 taylor series expansion에 대입합니다.
$y^{n+1}=y^{n}+\Delta t f\left(y^{n}, t^{n}\right)+\frac{\Delta t^{2}}{2 !}\left(f_{t}^{n}+f^{n} f_{y}^{n}\right)+\cdots$
또한 $k_{2}$를 $n$스텝에 대해 표현하기 위해 taylor expansion을 적용합니다.
$\begin{aligned} k_{2} &=\Delta t f\left(y^{n}+\beta k_{1}, t^{n}+\alpha \Delta t\right) \\ &=\Delta t f\left(y^{n}, t^{n}\right)+\Delta t \beta k_{1} f_{y}^{n}+\Delta t(\alpha \Delta t) f_{t}^{n}+\theta(\Delta t)^{3} \end{aligned}$
이제 여기서 구한 $k_{2}$를 $y^{n+1}=y^{n}+\gamma_{1} k_{1}+\gamma_{2} k_{2}$에 대입합니다.
$\begin{aligned} y^{n+1} &=y^{n}+\gamma_{1} k_{1}+\gamma_{2} k_{2} \\ &=y^{n}+\gamma_{1} \Delta t f\left(y^{n}, t^{n}\right)+\gamma_{2} \Delta t\left(f\left(y^{n}, t^{n}\right)+\beta k_{1} f_{y}^{n}+\alpha \Delta t f_{t}^{n}\right)+\cdots \\ &=y^{n}+\left(\gamma_{1} \Delta t + \gamma_{2} \Delta t\right) f\left(y^{n}, t^{n}\right)+\gamma_{2} \Delta t \beta k_{1} f_{y}^{n}+\gamma_{2}\Delta t \alpha \Delta t f_{t}^{n}+\cdots\\ &=y^{n}+\left(\gamma_{1}+ \gamma_{2}\right)\Delta t f\left(y^{n}, t^{n}\right)+ \gamma_{2} \Delta t^{2}\left(\beta f^{n} f_{y}^{n}+\alpha f_{t}^{n}\right)\end{aligned}$
이제 이 식을 exact solution인 위에서 구한 taylor series expansion과 비교합니다.
$y^{n+1}=y^{n}+\Delta t f\left(y^{n}, t^{n}\right)+\frac{\Delta t^{2}}{2 !}\left(f_{t}^{n}+f^{n} f_{y}^{n}\right)+\cdots$
최대한 accuracy를 높이기 위해 exact solution과 RK 방법 각 식의 계수를 일치시키도록 다음 식을 만족해야 합니다.
$\gamma_{1} \beta=\frac{1}{2}$
$\gamma_{1} \alpha=\frac{1}{2}$
$\gamma_{1}+\gamma_{2}=1$
이 방정식을 풀면
$\gamma_{1}=1-\frac{1}{2 \alpha}$
$\gamma_{2}=\frac{1}{2 \alpha}$
$\beta=\alpha$
처음에 제시했던 RK2 방법을 다시 생각해보겠습니다. 그 때는 시간 간격을 양 쪽이 같게 만들었었고, 따라서 $\alpha=1/2$일 때입니다. 그렇다면 $\beta = 1/2, \gamma_{1}=0, \gamma_{2}=1$이 나옵니다.
이 값을 식에 대입해보면 앞에서 했던 RK2 방법과 같다는 것을 알 수 있습니다.
$\alpha$는 0에서 1 사이의 임의의 값이므로 무수히 많은 2nd order RK 방법이 가능하게 됩니다. 또한 위의 exact solution과 비교했을 때 $\Delta t^{3}$의 오차가 나오므로 locally 3rd order accuracy임을 알 수 있습니다. globally 2nd order accuracy.
3. higher order Runge-Kutta method
위의 증명처럼 3차, 4차 늘려가면서 RK방법을 만들 수 있습니다.

이렇게 3개의 steps일 때는 $y^{n+1}=y^{n}+\gamma_{1} k_{1}+\gamma_{2} k_{2}+\gamma_{3} k_{3}$
다음처럼 식을 세워서 동일하게 풉니다.
사람들이 가장 무난하게 많이 쓰는 것은 RK4, 즉, 4th order Runge-Kutta 방법인데요.
이 경우에는 다음 식을 사용하는 것으로 알려져있습니다.
$y^{n+1}=y^{n}+\frac{1}{6} k_{1}+\frac{1}{3}\left(k_{2}+k_{3}\right)+\frac{1}{6} k_{4}$
$k_{1}=\Delta t f\left(y^{n}, t^{n}\right)$
$k_{2}=\Delta t f\left(y^{n}+\frac{1}{2} k_{1}, t^{n}+\frac{\Delta t}{2}\right)$
$k_{3}=\Delta t f\left(y^{n}+\frac{1}{2} k_{2}, t^{n}+\frac{\Delta t}{2}\right)$
$k_{4}=\Delta t f\left(y^{n}+k_{3}, t^{n}+\Delta t\right)$
RK4 방법은 globally 4th order accuracy도 매우 정확합니다.
또한 stability 영역은 다음과 같습니다. RK2는 Predictor-Corrector 방법과 동일하게 나오고, RK4는 Imaginary axis에 대해서도 stable 영역이 존재하기 때문에 explicit method도 imaginary 부분을 다루고 싶을 때 사용할 수 있습니다. (지금까지 배운 explicit method들은 불가능했습니다.)

Phase error 분석은 RK2만 적용하겠습니다.
$\sigma_{R k 2}=1+\lambda \Delta t+\frac{(\lambda \Delta t)^{2}}{2}$
$\lambda=i \omega$일 때
$\sigma_{RK_{2}}=1+i \omega \Delta t-\frac{\omega^{2} \Delta t^{2}}{2}$
$\theta=\tan ^{-1} \frac{\omega \Delta t}{1-\frac{\omega^{2} \Delta t^{2}}{2}}$
exact $-\theta=-\frac{(\omega \Delta t)^{3}}{6}$
phase error는 3차 수준으로 나게 됩니다.
여기까지 분석하고 마치도록 하겠습니다. 가능하면 RK4를 직접 유도해보는 것도 좋을 것이라 생각합니다.
'수치해석 Numerical Analysis' 카테고리의 다른 글
| [수치해석] Runge Kutta 4th order 증명 (0) | 2022.03.16 |
|---|---|
| [수치해석] Numerical solution of ODE (7) Leap frog method (0) | 2022.03.15 |
| [수치해석] Numerical solution of ODE (5) Predictor-Corrector Method (0) | 2021.09.26 |
| [수치해석] Numerical solution of ODE (4) Trapezoidal method (Crank-Nicolson) (0) | 2021.09.24 |
| [수치해석] Numerical solution of ODE (3) Implicit Euler (Backward Euler) (0) | 2021.04.29 |