ODE에 대한 Introduction에서 적분을 할 때 정해놓은 $\Delta t$가 아니라 그 안에서 여러 스텝을 거쳐서 적분을 하는 방법은 substep method이고, $t^{n+1}$라는 미래 시간을 계산하기 위해 현재와 그 이전 스텝을 쓰는 것을 multi step method라고 했습니다.
이번 글과 다음 글에서 소개할 방법은 multi step method의 범주에 드는 방법들입니다.

위의 그림처럼 $\Delta t$ 간격의 시간에서 $t^{n-1}$ 등 과거 스텝도 사용합니다.
이 방법에는 몇 가지 단점이 있습니다.
첫 번째, timestep size가 고정됩니다.
두 번째, self starting이 불가능합니다. 즉, 초기 조건을 알아도 그 초기 조건을 현재로 생각했을 때 이전 스텝도 알아야합니다.
그러나 장점도 있습니다. 한 번의 계산으로도 꽤 높은 정확도를 보이기 때문에 계산이 적다는 것입니다. (cost minimization)
이러한 multi step 방법 중 Leap frog method를 소개하도록 하겠습니다.
$\begin{aligned}&y^{\prime}=f(y, t) \\&\frac{y^{n+1}-y^{n-1}}{2 \Delta t}=f\left(y^{n},t^{n}\right)+\theta(\Delta t^{2})\end{aligned}$
이 식을 정리하면
$y^{n+1}=y^{n-1}+2 \Delta t f\left(y^{n}, t^{n}\right)+\theta\left(\Delta t^{3}\right)$
다음과 같으므로 이 방법의 정확도(accuracy)는 locally 3rd order이고 globally 2nd order입니다.
과거의 값만 사용하는 방법이기 때문에 explicit method라고 할 수 있습니다. 함수 계산이 한 번만 있는데도 locally 3rd order이기 때문에 계산 cost가 적다고 볼 수 있습니다.
leap frog method를 분석하기 위해 이전에 했던 것과 마찬가지로 model problem을 살펴보겠습니다.
$y^{\prime}=\lambda y$ 라고 할 때 위의 방법에 대입을 하면 다음과 같다.
$y^{n+1}=y^{n-1}+\lambda \Delta t f^{n} \Rightarrow y^{n}=\sigma^{n} y^{0}$
왼쪽 식을 보고 오른쪽 식의 형태로 만들고 싶지만 그러기는 어렵기 때문에 역으로 오른쪽 식을 왼쪽에 대입하여 $\sigma$를 구할 수 있다. 참고로 $f^{n}$은 $f$를 n번 곱했다는 뜻이 아니라 $f(x^{n},t^{n})$을 의미합니다.
$\sigma^{n+1} y^{0}=\sigma^{n-1} y^{0}-2 \Delta t \lambda \sigma^{n} y^{0}$
이제 위 식에서 $y^{0}$를 제거하면
$\sigma^{2}-2 \lambda \Delta t \sigma-1=0$
$\sigma=\lambda \Delta t \pm \sqrt{(\lambda \Delta t)^{2}+1}$
이렇게 2개의 $\sigma$를 구할 수 있습니다. $\sqrt{ (\lambda\Delta t)^{2} +1}$은 다항식으로 근사시킬 수 있습니다.
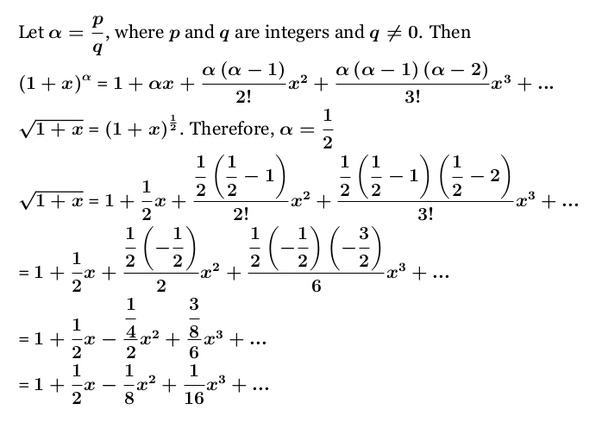
아주 옛날에 찾은 자료라서 어디에서 찾았는지 기억은 안나지만 위와 같이 근사가 가능합니다.
$\begin{aligned} \sigma_{1} &=\lambda \Delta t+1+\frac{1}{2}(\lambda \Delta t)^{2}-\frac{1}{8}(\lambda \Delta t)^{4}+\cdots \\ &=1+\lambda \Delta t+\frac{1}{2}(\lambda \Delta t)^{2}+\theta\left(\Delta t^{4}\right) \end{aligned}$
$\begin{aligned} \sigma_{2} &=\lambda \Delta t-1-\frac{1}{2}(\lambda \Delta t)^{2}+\frac{1}{8}(\lambda \Delta t)^{4}+\cdots \\ &=-1+\lambda \Delta t-\frac{1}{2}(\lambda \Delta t)^{2} +\theta\left(\Delta t^{4}\right) \end{aligned}$
여기서 Leap frog method의 문제점을 알 수 있습니다.
$\sigma_{2}$일 때를 가정하면
$y^{n}=(-1+\alpha)^{n}y^{0}$이고 이는 spurious(거짓된) solution입니다.
$\alpha$가 매우 작다고 했을 때 n에 따라서 $(-1)^{n}$이 음수였다가 양수였다가를 반복하기 때문입니다.
그렇게 되면 solution이 실제 결과와 달리 음수와 양수를 왔다갔다하는 모양새가 되므로 leaf frog 방법은 잘 사용하지 않는다고 합니다.
다만 저 $-1$의 영향을 없앨 수 있는 방법도 있습니다.
$y^{\prime}=\lambda y$
$y^{n+1}=y^{n-1}+\lambda \Delta t y^{n}$
$y^{n}=\left(c_{1} \sigma_{1}^{n}+c_{2} \sigma_{2}^{n}\right) y^{0}$
이 식을 이용해서 $n=0$일 때와 $n=1$일 때 연립을 합니다.
$\left.\begin{array}{ll}n=0 & y^{0}=c_{1}+c_{2} \\ n=1 & y^{1}=c_{1} \sigma_{1}+c_{2} \sigma_{2}\end{array}\right\} \quad \begin{array}{c}c_{1}=\frac{y^{1}-y^{0} \sigma_{2}}{\sigma_{1}-\sigma_{2}}\end{array}\quad c_{2}=\frac{-y^{1}+y^{0} \sigma_{1}}{\sigma_{1}-\sigma_{2}}=0$
$y^{0}-\sigma_{1} y^{\prime}=c_{2}\left(\sigma_{1}-\sigma_{2}\right)$
이 식에서 $c_{2}$를 보면 $c_{2}=0$일 때 $\sigma_{2}$의 영향이 없어지므로
$y^{1}=y^{0}\sigma_{1}$이면 됩니다.
하지만 긴 시간동안 적분을 하다보면 $\sigma_{1}$이 무한소수일 때 컴퓨터 상에서는 소수점 무한대까지 계산이 불가능해서 나중에는 솔루션이 망가지게 됩니다.
어쨌든, $\sigma$에 대해서 파악했으니 stability와 phase error에 대해서 알아보겠습니다.
$\lambda=\lambda_{R}+i\lambda_{I}$로 실수부와 허수부 모두 존재합니다.
만약 $\lambda=i\omega$, 즉 허수부만 존재하는 진동하는 시스템이라면 결과는 다음과 같습니다.
$\sigma_{1}=\lambda \Delta t+\sqrt{(\lambda \Delta t)^{2}+1}=\left|i \omega \Delta t+\sqrt{1-\omega^{2} \Delta t^{2}}\right|>1$
$\sigma_{2}=\lambda \Delta t-\sqrt{(\lambda \Delta t)^{2}+1}=\left|i \omega \Delta t-\sqrt{1-\omega^{2} \Delta t^{2}}\right|>1$
진동하는 시스템에서는 발산하는 결과가 나옵니다. 또한 꼭 $\lambda$가 허수부만 있는게 아니더라도 방법은 A-unstable, 즉 항상 unstable한 결과가 나옵니다. 두 $\sigma_{1},\sigma_{2}$가 1보다 작도록 하는 $\lambda$가 없기 때문입니다.
'수치해석 Numerical Analysis' 카테고리의 다른 글
| [수치해석] 미분방정식을 시간이 작아지는 방향으로(역으로) 풀 때 (0) | 2023.09.17 |
|---|---|
| [수치해석] Runge Kutta 4th order 증명 (0) | 2022.03.16 |
| [수치해석] Numerical solution of ODE (6) Runge-Kutta method (0) | 2021.09.26 |
| [수치해석] Numerical solution of ODE (5) Predictor-Corrector Method (0) | 2021.09.26 |
| [수치해석] Numerical solution of ODE (4) Trapezoidal method (Crank-Nicolson) (0) | 2021.09.24 |