* 이 글의 그림에서 사용된 아이콘은 모두 flaticon의 Freepik에서 나온 것입니다. 아래 링크로 들어가면 찾아볼 수 있습니다. User icons created by Freepik - Flaticon
Coordinated Turn
항공기의 coordinate turn은 slip, skid 없이 롤각으로 이루어지는 turn이다.
원운동하듯이 일정 요각 변화율($\dot{\psi}$)로 움직이고 있는 비행기가 있을 때 이 요각 변화율은 bank angle 덕분에 만들어진 것이다.

일정 요각 변화율로 turn을 하고 싶다면 다음 조건이 만족해야한다.
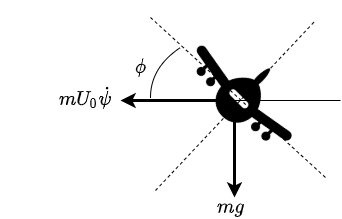
$mU_{0}\dot{\psi} \cos\phi = mg\sin \phi$
$\Rightarrow \tan\phi =\frac{U_{0}\dot{\psi} }{g} $
$mU_{0}\dot{\psi}$는 구심력 식에서 사용되는 $mr\omega ^{2}=m\frac{mv^{2}}{r}=mv\omega$
중력을 비행기의 Y축에 대해서 projection할 때 이 힘이 곧 원운동할 때 작용하는 구심력이 되고, 이 구심력과 원하는 요각 변화율에 의해 계산되는 원심력은 같다.
애초에 원심력은 가상의 힘이므로, 중력의 Y축 방향 힘이 구심력으로 작용해서 원운동을 하고 있다고 봐도 된다.
만약 위 식이 만족하지 않는 경우를 생각해보자. 중력으로 발생하는 구심력보다 더 빠르게 요각 변화가 일어난다는 등의 상황에서는 coordinated turn이 성립하지 않는다.
따라서 원하는 coordinated turn을 만들기 위해서는 적절한 bank angle을 가져야하고 이를 위해 롤각 제어기가 필요하게 된다.
Additional question :
비행기 안에 타고 있는 사람은 coordinated turn일 때 어디로 쏠리게 될까?
정답 먼저 말하면 아무데도 쏠리지 않는다.
우리가 물리에서 배운대로 비행기 내부에 있는 사람은 비행기가 coordinated turn을 하는 것을 인식하지 못하고 대신 관성력을 도입하여서 운동을 설명한다.
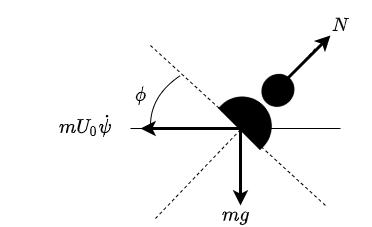
다음 그림처럼 비행기 내부에 있는 사람은 자신의 질량에 따른 중력이 있을 것이고, 자리에 앉아있으므로 비행기가 사람에게 작용하는 수직항력($N$)이 작용한다. 이 수직항력은 비행기가 어떤 운동을 하느냐에 따라 다를 것이다. 그리고 이 수직항력, 중력만 존재하면 사람은 오른쪽 방향으로 쏠리는 느낌을 받게 된다.
그러나 coordinate turn에서는 바깥쪽으로 향하는 원심력까지 도입되어 사람은 균형을 이루게 된다.
* 참고로 헷갈릴까봐 말하자면, '특정 힘'이 원운동을 위해 작용할 때 그 힘이 구심력처럼 작용한다고 말하는 것이지 애초부터 구심력이라는 힘은 존재하지 않는다고 볼 수 있다. 예를 들어 공에 실을 매달아서 원운동을 할 때 장력이 구심력 역할을 하는 것인 것처럼 말이다.
위에서 얘기했던 것처럼 이런 균형이 맞지 않으면 안에 있는 사람은 왼쪽이나 오른쪽으로 쏠리는 느낌을 받게 될 것이다.
구심력과 원심력 탐구 : 롤러코스터 문제
여기서 좀 더 나아가서 아주 고전적인 문제인 롤러코스터 문제를 생각해볼 수 있다.
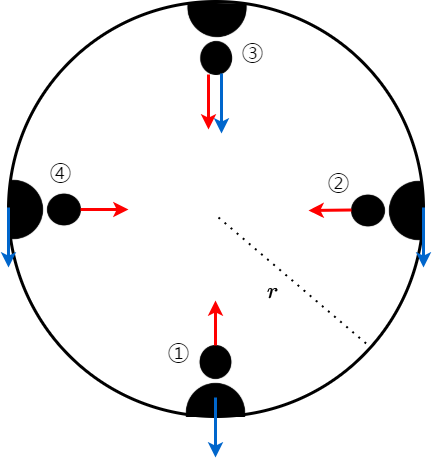
위 그림에서 파란색 화살표는 중력 $mg$을 의미하고, 빨간색 화살표는 수직항력 $N$을 의미한다.
1번 상황에서 사람에게 작용하는 힘은 위 방향이 양수라고 생각하고 $N_{1}-mg$만큼 작용한다.
2번 상황은 수직항력은 원의 중심 방향으로, 중력은 아래 방향으로 작용하기 때문에 두 힘이 나란하게 작용하지는 않는다.
3번 상황은 아래 방향으로 중력과 수직항력이 작용하게 된다.
4번 상황은 수직항력은 원의 중심 방향으로, 중력은 아래 방향으로 작용한다.
여기서 의문을 가져야할 부분은 3번이다. 3번을 보면 분명 중력과 수직항력 모두 아래를 향하므로 사람이 떨어져야하는 것이 맞다. 그러나 롤러코스터를 타다가 아래로 뚝 떨어진다면 롤러코스터는 운영될 수 없었을 것이다.
즉, 어떤 힘이 사람을 떨어지지 않게 막아주고 있고 이 힘을 롤러코스터에 탄 사람 기준으로는 '원심력'이 작용하기 때문이라고 볼 수 있다.
원심력은 원의 중심으로 향하는 방향의 반대방향으로 작용하므로, 이 힘이 중력을 이겨내고 사람을 롤러코스터에 붙어있을 수 있게 만드는 힘이다.

그러면 이 롤러코스터는 수직항력이 없다고 생각하고 중력만 고려하면 $mg = mr\omega^{2}=m\frac{v^{2}}{r}$가 성립해야된다. ($r$은 원의 반지름, $\omega$는 각속도) 만약 원운동할 때 각속도가 더 빠르면 그만큼 수직항력이 커지면 되므로 괜찮지만, 그보다 각속도가 느리면 안된다.
따라서 최소한 롤러코스터의 정점에서 속력이 $v=\sqrt{gr}$(또는 각속도 $\omega = \sqrt{\frac{g}{r}}$)는 되어야 한다.
그리고 만약 $v=2\sqrt{gr}$이라고 해보자. 최소 속력보다 더 큰 경우이다. 이 경우에는
$N+mg = m\frac{4gr}{r}=4mg$ 이므로 수직항력이 $3mg$로 작용한다.
참고로 위의 롤러코스터는 등속원운동 문제라고 생각하면 안된다.
2번과 4번 상태를 보면 중력이 수직항력과 별개로 아래로 작용하므로 2번을 거치는 과정에서는 속력이 느려지도록 힘을 받고, 4번을 거치는 과정에서는 속력이 빨라지도록 힘을 받는다. 따라서 가장 높은 점으로 올라가고 내려가는 과정에서 몸이 가속되고 감속되는 것을 느낄 것이다.
이런 해석에서 중요한 점은 구심력이 따로 있다고 생각하는 것이 아니라, 원의 중심으로 향하는 힘이 곧 구심력처럼 작용하여 속도의 방향을 바꾸고, 속력은 구심력 외의 다른 힘에 의해서 증가하거나 감소한다는 것이다.
그래서 마찰이 없는 환경이라면, 힘보다는 에너지로 해석하는 것이 더 나을 수 있다.
'항공우주 Aeronautical engineering' 카테고리의 다른 글
| [비행동역학] Multicopter (Drone) dynamics (1) | 2023.11.08 |
|---|---|
| [비행동역학] Total angle of attack and Aerodynamic roll angle (0) | 2022.08.08 |
| [추진] 추진공학에 대한 개요 (2) 분류 (0) | 2022.03.02 |
| [추진] 추진공학에 대한 개요 (1) 기본 원리 (0) | 2022.02.25 |
| [항법] 쿼터니언 Quaternion (2) 쿼터니언 미분과 업데이트 식 (0) | 2022.01.25 |