angle of attack은 바람에 대한 상대적인 속도를 나타낼 때 사용된다. 공력을 표시할 때 공력은 바람에 대한 상대속도를 기준으로 만들어지기 때문이다.
그 중에서도 total angle of attack ($\alpha_{T}$)과 aerodynamic roll angle ($\phi_{T}$)이라는 개념이 있다. 이 개념은 angle of attack, side slip angle과 달리 XY평면, XZ평면 대칭인 미사일 같은 형상을 다룰 때 사용된다. (AoA와 Side slip angle은 비행기 같은 XZ평면 대칭인 경우에 주로 사용된다.)
$\alpha_{T} = \cos^{-1}(\cos\alpha \cos\beta)$
$\phi_{T}=\tan^{-1}\left(\displaystyle \frac{\tan\beta }{\sin\alpha} \right)$
여기서 $\alpha$와 $\beta$는 받음각과 옆미끄럼각이다.
$\alpha=\tan^{-1}\left( \displaystyle \frac{w}{u} \right),\; \beta=\sin^{-1}\left(\displaystyle \frac{v}{V}\right)$
위의 정의 말고도 기하학적인 형상을 보고도 다음과 같이 구할 수 있다.
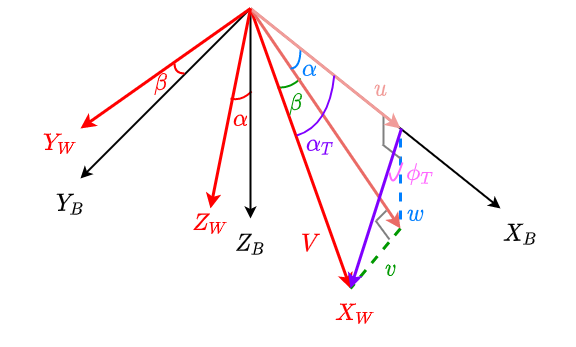
위 그림에서 빨간색은 바람을 기준으로 한 좌표계이다.
$u,v,w$는 동체 좌표계를 기준으로 표기한 물체의 속도이다.
위 그림에 따르면,
$\alpha_{T}=\cos^{-1}\left(\displaystyle \frac{u}{V}\right)$
$\phi_{T}=\tan^{-1}\left(\displaystyle\frac{v}{w}\right)$
으로 구할 수 있다.
Q. 그러면 $(\alpha, \beta)$와 $(\alpha_{T},\phi_{T})$의 변환을 쉽게 구할 수 있는 방법이 있을까?
$\alpha, \beta$가 주어진 경우에는 위의 식을 이용해 바로 $\alpha_{T},\phi_{T}$를 구할 수 있지만 역으로는 구하기 어렵다.
그래서 차라리 중간 단계인 $(u,v,w,V)$를 구하고 그 다음에 $\alpha,\beta$를 구하는 방법이 있다.
$V=1$로 고정시켜놓으면 구속조건으로 $u^2+v^2+w^2=V^2=1$이 생긴다.
$ \cos\alpha_{T}=\displaystyle \frac{u}{V} $
$ \tan\phi_{T}=\displaystyle\frac{v}{w} $
를 만족하는 $u,v,w$를 쉽게 구할 수 있다.
$u = V\cos\alpha_{T}$
$w\tan\phi_{T}=v$
이 식을 구속조건에 대입하면,
$V^2 \left((1-\cos\alpha_{T})^2\right) = w^2 \left(1+(\tan\phi_{T})^2\right)$
여기서 $w$를 구할 수 있고, $u$는 이미 $u = V\cos\alpha_{T}$ 관계로 알 수 있으며,
자동으로 $v$가 결정된다.
그 다음에는 이 식으로 구하면 된다
$\alpha=\tan^{-1}\left( \displaystyle \frac{w}{u} \right),\; \beta=\sin^{-1}\left(\displaystyle \frac{v}{V}\right)$
# MATLAB 코드
alpt = [ 0, 4, 8, 12, 16 ] ;
phia = [ 0. , 22.5, 45. , 67.5, 90. , 112.5, 135. , 157.5, 180. ,...
202.5, 225. , 247.5, 270. , 292.5, 315. , 337.5, 360. ] ;
N = length(alpt) ;
M = length(phia) ;
R2D = 180.0/pi ;
options = optimoptions('fsolve','Display','off') ;
record = zeros(length(alpt)*length(phia),2) ;
V = 1 ;
for i =1:N
fprintf(" ====================================================================== \n") ;
for j =1:M
alpt_tmp = alpt(i) ;
phia_tmp = phia(j) ;
fprintf("when alpt = %.1f, phia = %.1f / ", alpt_tmp, phia_tmp) ;
w = sqrt( (1 - V^2 * cosd(alpt_tmp)^2) / (1+tand(phia_tmp)^2) ) ;
u = V * cosd(alpt_tmp) ;
v = sqrt(1-w^2-u^2) ;
alpha = atan(w/u) * R2D ;
beta = asin(v/V) * R2D ;
fprintf(" u = %.2f, v = %.2f, w = %.2f / ", u,v,w)
fprintf(" alpha = %.2f, beta = %.2f \n", alpha, beta) ;
record( (i-1)*M + j, 1 ) = alpha ;
record( (i-1)*M + j, 2 ) = beta ;
end
end
'항공우주 Aeronautical engineering' 카테고리의 다른 글
| [비행동역학] Multicopter (Drone) 제어기 (0) | 2023.12.04 |
|---|---|
| [비행동역학] Multicopter (Drone) dynamics (1) | 2023.11.08 |
| [비행동역학] Coordinated turn과 원심력, 구심력에 대한 고찰 (0) | 2022.03.12 |
| [추진] 추진공학에 대한 개요 (2) 분류 (0) | 2022.03.02 |
| [추진] 추진공학에 대한 개요 (1) 기본 원리 (0) | 2022.02.25 |