사실 물체의 dynamics 자체는 뉴턴 법칙으로 고정되어있기 때문에 익숙하다.
다만 이 dynamics에서 얼마만큼 더 '정밀하게' 모델링할 것인가는 엔지니어의 몫이다.
예를 들면
$\dot{P}=F$
$\dot{H}=M$
다음과 같이 운동량의 변화율은 힘이고, 각운동량의 변화율은 모멘트 (즉, 힘과 모멘트로 운동량/각운동량을 변화시킬 수 있다)라는 사실은 변하지 않는다. 하지만 제어하는 사람 입장에서는 이 힘이 어떻게 발생하는지를 디테일하게 따져보게 된다.
일례를 들면, 지금 설명할 드론의 경우 공기로 인한 항력이 발생할 수 있다. 나는 이런 유체역학을 기초적인 부분 밖에 모르지만 모터가 돌면 주변의 발생하는 바람으로 인해 힘에 영향을 줄 수 있다. 하지만 측정이 불가능한 영역이라면 이를 무시하고 dynamics를 구성하게 되는 것이다.
1. Multicopter dynamics
Dynamics를 기술할 때 가장 중요한 것은 좌표계 문제이다. 좌표계에 대해서 옛날에 고민을 많이 하고 쓴 글이 있으니 참고하실 분들은 참고하시길. (링크)
1) Translation dynamics
멀티콥터는 구조상 body 기준으로 z축 방향으로밖에 힘을 만들 수 없다. 이 점 때문에 제어기 설계 로직에도 영향을 주게 된다.
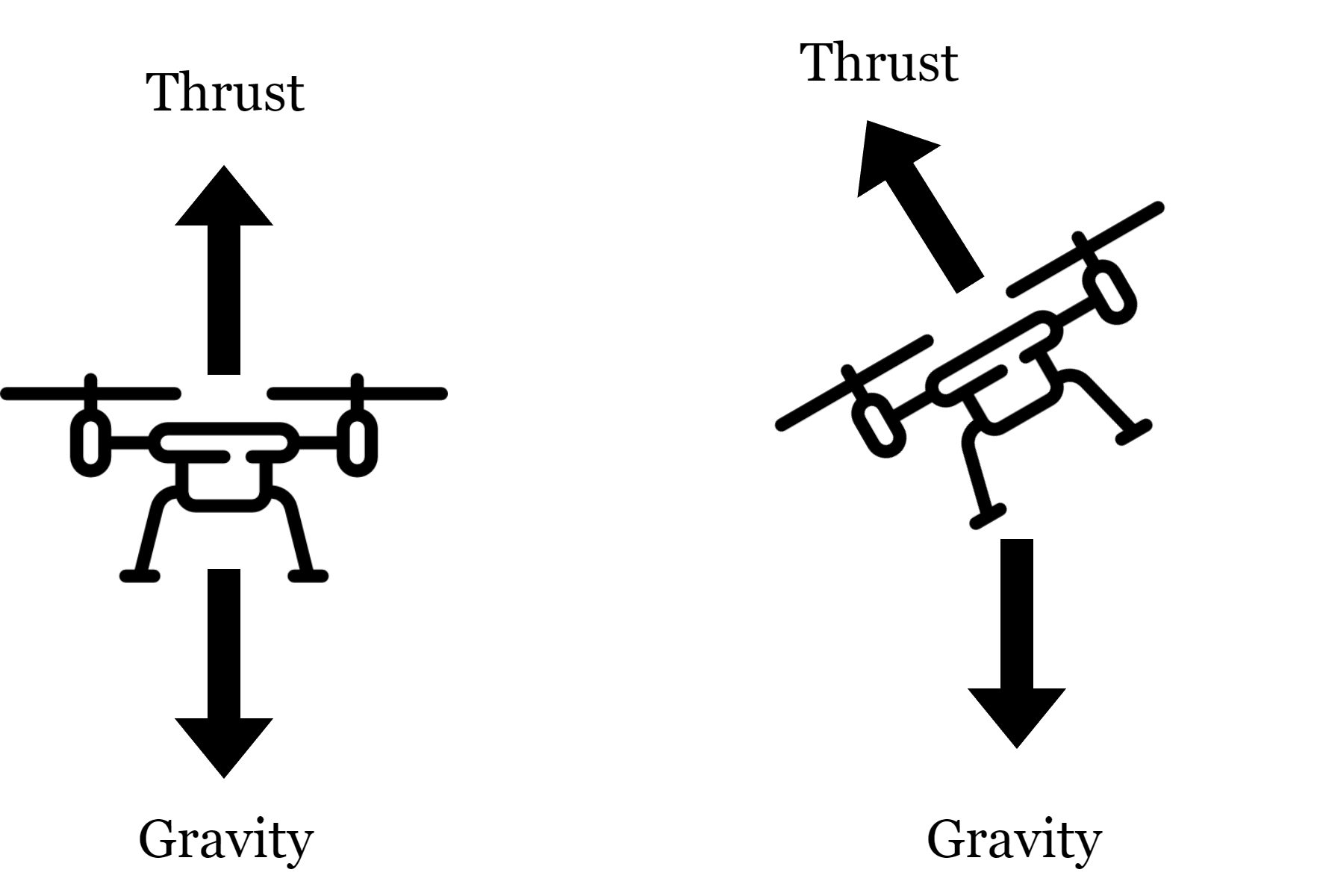
기본적으로 $m\dot{v}=m \ddot{x} = F$로 구성이 되며, 멀티콥터에 작용하는 힘은 대표적으로 동체 z축방향 Thrust가 있다. 또한 중력은 항상 지구 중심 방향을 가리키고 있다.
관성 좌표계에서 동체 좌표계로 변환하는 DCM을 구해야하는데 이는 오일러각을 기반으로 구할 수 있다.
Direction Cosine Matrix (DCM) 은 다음과 같다. (유도 과정은 다음 글 참고)
\begin{equation}
[C]_{I}^{B}=\left[\begin{array}{ccc}
\cos \psi \cos \theta & \cos \psi \sin \theta \sin \phi-\cos \phi \sin \psi & \cos \psi \sin \theta \cos \phi+\sin \phi \sin \psi \\
\sin \psi \cos \theta & \sin \psi \sin \theta \sin \phi+\cos \phi \cos \psi & \sin \psi \sin \theta \cos \phi-\sin \phi \cos \psi \\
-\sin \theta & \sin \phi \cos \theta & \cos \theta \cos \phi
\end{array}\right]
\end{equation}
따라서 body 기준으로 작용하는 추력 벡터 $F_{B}=[0,0,T]^{\top}$을 DCM을 통해 관성좌표계 기준으로 바꿔준다.
$$ F_{I}=C_{I}^{B}\times F_{B}$$
그리고 중력 외에 작용하는 다른 힘은 관성좌표계 기준으로 $[f_{x}, f_{y}, f_{z}+g]^{\top}$으로 표현한다. 모델링 정도에 따라 이 힘을 얼마나 구체적으로 나타낼지가 결정될 것이다. 주로 $f$에 포함되는 것은 항력인데 항력 모델링은 시스템에 따라 차이가 있다.
$f_{x}=-d_{x}\dot{x}, f_{y}=-d_{y}\dot{y}, f_{z}=-d_{z}\dot{z}$
다음과 같이 속도에 항력 계수만큼 비례하게 모델링할 수도 있고, 공력에 의한 항력처럼 속력의 제곱에 비례하게 설정할 수도 있다.
\begin{equation}
\left[\begin{array}{c}
\ddot{x} \\
\ddot{y} \\
\ddot{z}
\end{array}\right]=\frac{1}{m}\left[\begin{array}{c}
F_x+f_x \\
F_y+f_y \\
F_z+g+f_z
\end{array}\right]=-\frac{T}{m}\left[\begin{array}{c}
\cos \psi \sin \theta \cos \phi+\sin \phi \sin \psi \\
\sin \psi \sin \theta \cos \phi-\sin \phi \cos \psi \\
\cos \theta \cos \phi
\end{array}\right]+\left[\begin{array}{c}
f_x \\
f_y \\
g+f_z
\end{array}\right]
\end{equation}
2) Rotational dynamics
$M=\dot{H}=\dot{H}_{I}+\omega\times H= I\dot{\omega}+\omega \times H_{I} \quad (H_{I}=I\omega)$
동역학에서 관성좌표계에서 보는 회전하는 물체의 운동을 기술할 때 위와 같이 나오는데 유도과정은 이 글에 나와있다.
위에서 $I$는 mass moment of inertia matrix이고 운동 중에 변하지 않는다고 하자.
$I=\begin{bmatrix}I_{xx} & I_{xy} & I_{xz} \\ I_{yx} & I_{yy} & I_{yz} \\ I_{zx} & I_{zy} & I_{zz} \end{bmatrix}$
$\dot{\omega} = I^{-1}(M-\omega \times H)$
멀티콥터의 경우에는 xz, yz 평면 대칭이므로 $J$에서 diagonal term만 존재한다고 생각할 수 있다.
$$ \left[\begin{array}{c}
\dot{p} \\
\dot{q} \\
\dot{r}
\end{array}\right] = \left[\begin{array}{c}
\dfrac{I_{yy}-I_{zz}}{I_{xx}}qr \\
\dfrac{I_{zz}-I_{xx}}{I_{yy}}pr \\
\dfrac{I_{xx}-I_{yy}}{I_{zz}}pq
\end{array}\right] + \left[\begin{array}{c}
\dfrac{M_{1}}{I_{xx}}\\
\dfrac{M_{2}}{I_{yy}} \\
\dfrac{M_{3}}{I_{zz}}
\end{array}\right] $$
여기서 Moment를 만들 수 있는 것은 멀티콥터의 추력 차이로 발생시키는 모멘트와 로터 자체에서 발생하는 회전력 등이 있다.

각 부분에서 작용하는 힘을 $F_{1},F_{2},F_{3},F_{4}$라고 하자. 앞서 translational dynamics에서 봤던 것은 $T=F_{1}+F_{2}+F_{3}+F_{4}$이다.
$$M_{1}=L_{y}F_{1}-L_y F_{2}+L_{y}F_{3}-L_{y}F_{4}$$
$$M_{2}=L_{x}F_{1} +L_{x}F_{2} -L_{x}F_{3} -L_{x}F_{4} $$
Yawing moment의 경우에는 모터 모델에서 구한 torque coefficient를 사용해야한다.
모터 모델에 대한 내용은 아래로 이어진다.
$$M_{3}=-c_{Q}(F_{1} +F_{2} +F_{3} -F_{4}) \quad \text{ where } c_{Q}=\left( \dfrac{k_{Q}}{k_{T}}\right)$$
참고로 이 요 모멘트와 힘과의 관계식은 아래의 모터 모델에 따라 결정된 값이다.
즉, 각 모터의 요 모멘트가 $F_{1},F_{2},F_{3},F_{4}$에 비례하는 값으로 모델을 결정했기 때문이며, 정확히는 모터의 회전수에 따라 결정되는 값이고 모터의 힘 역시 회전수에 따라 결정되기 때문에 위와 같이 계산할 수 있다.
3) 모터 모델
모터의 자체의 추력과 토크는 다음과 같은 관계를 갖는다.
$$T=k_{T}\Omega^{2}$$
$$Q=k_{Q}\Omega^{2}$$
여기서 $\Omega$는 모터의 RPM을 의미하고 $k_{T},k_{Q}$는 thrust, torque coefficient이다. 이 계수는 블레이드의 형상 등에 따라 달라지는 부분이다.
이렇게 관계가 도출된 이유는 실험적인 결과로 뒷받침된다.
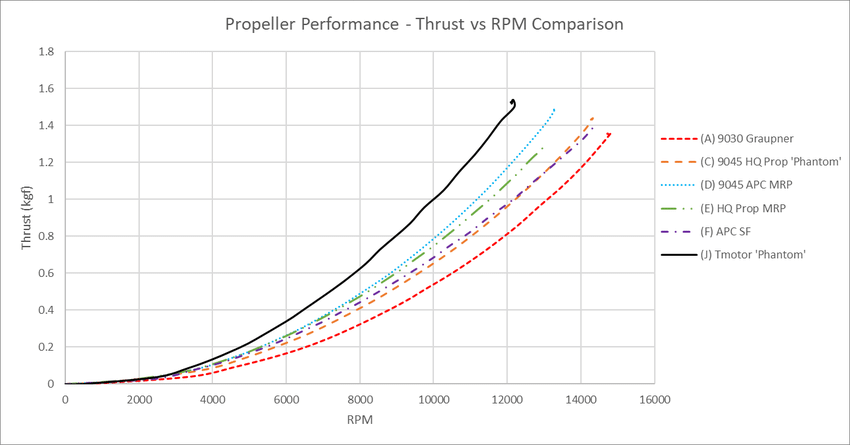
많은 모터가 대략적으로 rpm과 추력 간의 quadratic function 관계로 근사될 수 있기 때문이다.
토크 역시 비슷할 것이라고 가정하고 계산하는데 아직까지 실험적 결과는 찾지 못했다. 또한 이런 Thrust & torque coefficient를 구하는 이론적인 식도 연구에서 나와있다. 보통은 시스템 식별을 통해서 구한다.
4) 종합
종합해서 보면 x,y,z 축으로 움직이는 경우, 즉 평면 상과 고도 상으로 움직이고 싶은 경우에는 로터 자체의 추력을 바꿀 수 있다. 하지만 x,y를 변화시키고 싶으면 추력의 크기 뿐 아니라 자세각을 조절해야한다.
자세각을 바꾸는 방법은 로터 각각의 추력을 제어해서 모멘트를 만들고 이 모멘트로 각속도를 변화시켜 최종적으로는 각도를 변화시켜야 한다.
이 설명에서 중요한 점은 제어 순서이다. 보통 response가 빠른 것이 inner loop로 제어하고, response가 느린 것이 outer loop로 제어하며 위의 설명대로 각속도를 먼저 건드려야 각도 제어, 속도제어, 위치제어로 이어질 수 있다.
이 생각을 바탕으로 제어기를 설계한다.
2. 제어기 설계 구조
구체적인 제어기는 나중에 pixhwak 사 얘기를 하면서 더 구체적으로 얘기할 것으로 보인다.
제어기 설계 원칙에 따라 다를 수 있는 있겠으나
기본적으로 가장 response가 빠른 부분이 내부에 들어가게 된다.
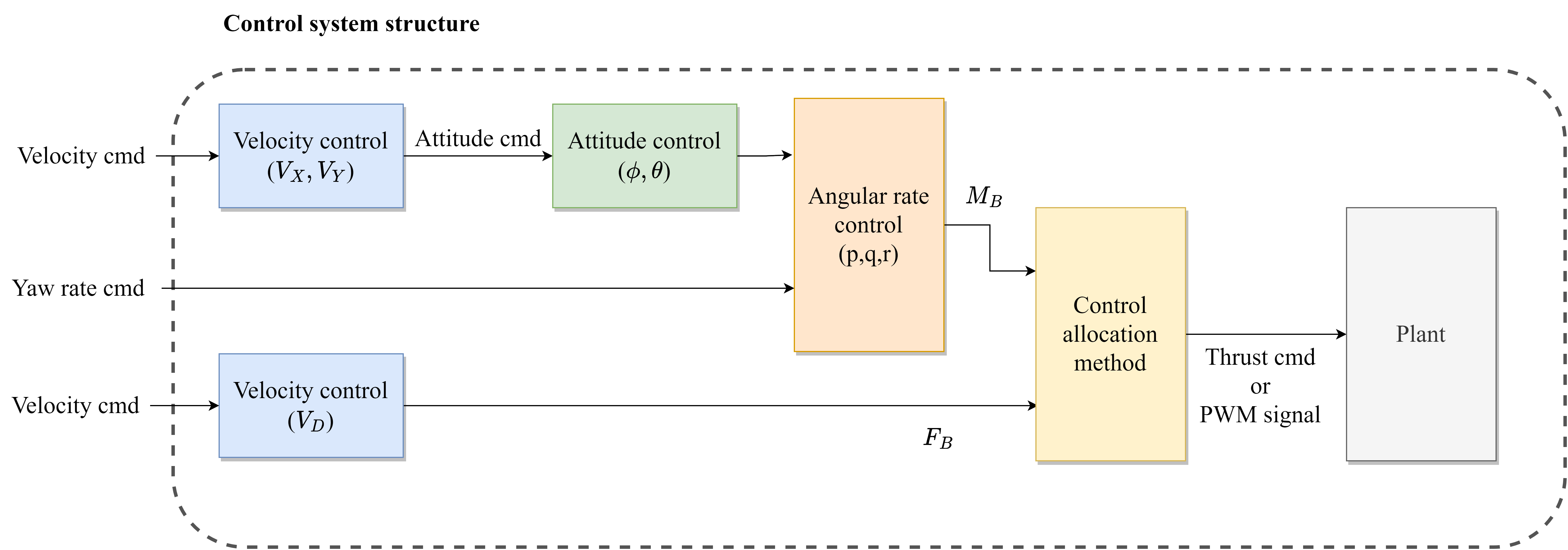
따라서 아래 그림과 같이 속도 제어 - 자세 제어 - 각속도 제어 순서로 제어를 하게 된다.
또한 결국 개별 모터에 들어가는 명령은 PWM 신호로 들어가기 때문에 이를 Mapping해주는 로직을 정해야한다.
여기서는 Control allocation method는 무엇이 있느냐고 하면, 제어기처럼 설계 방식에 따라 달라질 수 있다.
드론 이미지 사용 : 드론 케이스 아이콘 제작자: Freepik - Flaticon 무인 비행기 아이콘 제작자: surang - Flaticon
12,043,689종의 무료 아이콘
SVG, PSD, PNG, EPS 포맷 또는 웹폰트로 제공되는 12,043,689종 이상의 아이콘을 다운로드받으세요. 최대의 무료 아이콘 데이터베이스 - Flaticon.
www.flaticon.com
'항공우주 Aeronautical engineering' 카테고리의 다른 글
| [항공우주] Guidance, Navigation, and Control (GNC)란 무엇인가 (0) | 2023.12.07 |
|---|---|
| [비행동역학] Multicopter (Drone) 제어기 (0) | 2023.12.04 |
| [비행동역학] Total angle of attack and Aerodynamic roll angle (0) | 2022.08.08 |
| [비행동역학] Coordinated turn과 원심력, 구심력에 대한 고찰 (0) | 2022.03.12 |
| [추진] 추진공학에 대한 개요 (2) 분류 (0) | 2022.03.02 |