이런저런 생각을 하다가 미분방정식의 최종 시간에서의 값이 정해질 때 역으로 풀면 (즉, 시간을 거꾸로 해서 풀면)
풀릴 지에 대한 궁금증이 생겨서 테스트한 것이다.
% Solve differential equation using MATLAB odesolver
tspan = [0 5];
y0 = 10;
[t,y] = ode45(@(t,y) -2*y, tspan, y0);
figure;
plot(t,y,'-o');
dt = 0.01 ;
N = tspan(2) / dt ;
x = zeros(N+1,1) ;
f = @(t,y) -2*y ;
x(1) = y(end) ;
% solve reversely
for i =1:N
t_tmp = 5 - dt * i ;
x(i+1) = x(i) - dt * f(t_tmp,x(i)) ;
end
Time = 0 : dt : tspan(2) ;
x_flip = flipud(x) ;
figure; hold on;
plot(t,y,'-o');
plot(Time,x_flip') ;
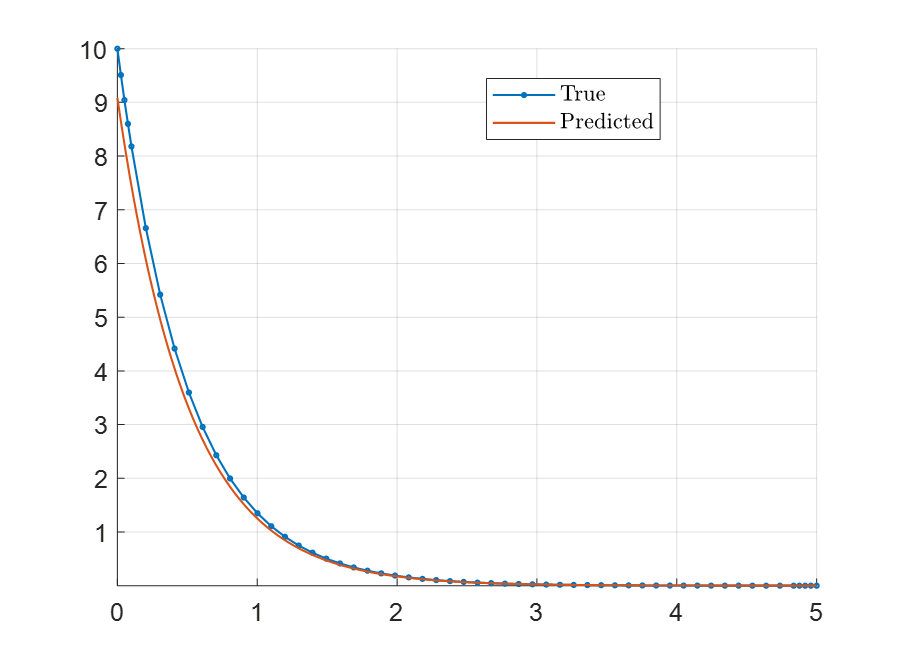
legend('True','Predicted') ;
다음과 같이 계산할 때 True값과 어느정도 비슷한 경향을 보인다. 시스템이 단순해서 이렇게 나오는 것 같아서 좀 더 복잡한 시스템에 대해서도 테스트해볼 생각이다.
'수치해석 Numerical Analysis' 카테고리의 다른 글
| [수치해석] System of ODEs - Boundary value problem (0) | 2025.07.20 |
|---|---|
| [수치해석] System of ODEs - Initial value problem (0) | 2025.07.20 |
| [수치해석] Runge Kutta 4th order 증명 (0) | 2022.03.16 |
| [수치해석] Numerical solution of ODE (7) Leap frog method (0) | 2022.03.15 |
| [수치해석] Numerical solution of ODE (6) Runge-Kutta method (0) | 2021.09.26 |