MATLAB에서는 친절하게 State space model과 transfer function 간에 전환하기 쉽도록 되어 있습니다.
그러다보니 굳이 원리를 몰라도 state space model에서 transfer function으로 바꿀 수도 있고, 반대도 가능합니다만,
저는 원리를 다 알아보고 가겠습니다.
0. System의 input과 output의 관계

어떤 LTI 시스템에서 input u(t)을 넣었을 때 output y(t)를 구하는 방법은, u(t)*g(t) (g(t) : Impulse response)를 수행하는 것입니다. 즉, u(t)와 g(t)를 convolution하는 방법입니다.
이는 frequency domain 또는 s domain에서 쉽게 곱셈으로 풀 수 있기 때문에, time domain에서 frequency domain, s domain으로 바꾸는 fourier transform, laplace transform이 유용한 것입니다.
즉, $y(t)=u(t)*g(t) \Leftrightarrow Y(s)=G(s)U(s) \Leftrightarrow \frac{Y(s)}{U(s)}=G(s)\text{ : transfer function}$
1. State Space to Tranfer Function (SS2TF)
State Space model에서 Transfer Function으로 바꾸는 것은 Laplace transform을 통해 간단히 할 수 있습니다.
$ \frac{dx(t)}{dt} = Ax(t) + Bu(t)$
$ y(t) = Cx(t) + Du(t)$
위의 식을 Laplace transform합니다.
$ sX(s) -x(0) = AX(s) + BU(s)$
$(sI-A)X(s) = BU(s)$ (initial condition은 0으로 두고 식을 풉니다.)
$X(s)=(sI-A)^{-1}BU(s)$
$Y(s)=CX(s)+DU(s)$ 이므로 위의 식을 이 식에 대입합니다.
$Y(s)=[C(sI-A)^{-1}B+D]U(s)$
이를 통해 $\frac{Y(s)}{U(s)}$, 즉 transfer function을 구할 수 있습니다.
$\frac{Y(s)}{U(s)}=G(s)=[C(sI-A)^{-1}B+D]=\frac{B(s)}{A(s)}$
A(s)는 characteristic equation, 특성방정식이라 해서 A(s)=0이 되는 s의 값을 pole이라고 합니다.
B(s)=0이 되는 s의 값을 zero라고 합니다.
Example
이전에 작성한 예시를 풀어보면(링크에 들어가서 5번 항목으로 가시면 됩니다. normal-engineer.tistory.com/24)
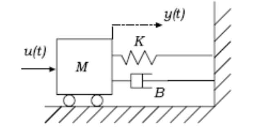
이 시스템의 DE는
$M\ddot{y}+B\dot{y}+Ky=u$
$\ddot{y}=\ddot{p}=\dot{v}=-\frac{B}{M}\dot{p}-\frac{K}{M}p+\frac{1}{M}u$
그리고 State-space model은
$A =\begin{bmatrix}0&1\\-\frac{K}{M}&-\frac{B}{M}\end{bmatrix} \in \Re^{2\times2}$
$B =\begin{bmatrix}0\\ \frac{1}{M}\end{bmatrix} \in \Re^{2\times1}$
$C =\begin{bmatrix}1&0\end{bmatrix} \in \Re^{1\times2}$
$D = 0$
다음과 같이 나왔습니다.
DE를 Laplace transform하여 구한 transfer function은 $\frac{1}{Ms^{2}+Bs+K}$이고,
위의 State space model에서 transfer function으로 바꾸는 공식을 쓰면 아래와 같습니다.

맨아래 결과와 같이 동일하게 transfer function을 구할 수 있습니다.
2. From Transfer Function to State Space(TF2SS)
State space에서 transfer function으로 바꾸어보았으니, transfer function에서 state space로도 바꿀 수 있을 것 같다는 생각이 듭니다.
하지만 여기서 맹점이 있습니다. 이전에 state space와 관련한 글에서, state variables의 갯수는 고정되어 있지만 state vector를 구성하는 조합은 무한히 많다고 했습니다. 그리고 state vector에 따라서 A,B,C,D matrix가 바뀌기 때문에 transfer function을 state space로 바꿀 때도 무한히 많은 A,B,C,D의 조합이 생길 것이라고 추측해볼 수 있습니다.
이 글에서는 state space로 바꿀 때 무수히 많은 형태 중 크게 3가지 형태로 바꾸는 법에 대해 배웁니다.
1) Controllable canonical form
2) Observable canonical form
3) Jordan form
* D가 0이 아닌 경우 (즉, Transfer function의 분자와 분모의 차수가 일치하는 경우)
$G(s) = \frac{b_{2}s^{2}+b_{1}s+b_{0}}{s^{3}+a_{2}s^{2}+a_{1}s+a_{0}}+D$
이 경우는 input이 직접적으로 output에 관여하는 경우인데, 보통의 mechanical system에서 D=0이다. D가 0이 아닌 경우는 매우 드문 상황이다.
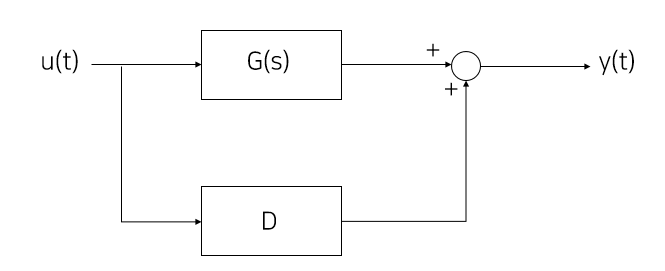
그렇다면 분자의 차수가 분모보다 높은 경우도 있을까?
예를 들면 다음과 같은 시스템을 생각해보자.$y=\dot{u}$$Y(s)=sU(s)$$G(s)=\frac{Y(s)}{U(s)}=\frac{s}{1}$이 경우는 분모가 분자보다 차수가 높은 경우다. Laplace transform에서 s를 곱하는 것은 미분할 때인데, 실제 input을 미분을 하기 위해서는 미래의 값을 알아야하므로 causal한 경우에는 사용할 수 없다. 즉 현실 세계의 mechanical system은 causal이므로 s가 존재할 수 없다.
즉 우리가 보는 대부분의 transfer function은 분모의 차수가 분자보다 높다.
3. Controllable Canonical form
시스템의 controllability는 다른 문서에 작성하고, 따로 링크를 첨부하도록 하겠습니다.
그래도 이야기하기 앞서, 간단하게 controllabilty에 대해서 말하겠습니다. 시스템을 설계를 할 때, input에 대하여 모든 원하는 output을 얻을 수 있는 것은 아닙니다. 시스템 특성에 따라서 아무리 제어기를 바꿔도 안될 수도 있습니다. 그럼에도 불구하고 input을 조절하여 어떤 final state를 얻을 수 있을 때 controllable system이라고 합니다.
Transfer function G(s)가
$G(s)=\frac{B(s)}{A(s)}=\frac{b_{2}s^{2}+b_{1}s+b_{0}}{s^{3}+a_{2}s^{2}+a_{1}s+a_{0}}$이라고 할 때,
Controllable Canonical form은 다음과 같습니다.
$\frac{d}{dt}\begin{bmatrix}x_{1}\\x_{2}\\x_{3}\end{bmatrix}=\begin{bmatrix}0&1&0\\0&0&1\\-a_{0}&-a_{1}&-a_{2}\end{bmatrix}\begin{bmatrix}x_{1}\\x_{2}\\x_{3}\end{bmatrix}+\begin{bmatrix}0\\0\\1\end{bmatrix}u$
$y=\begin{bmatrix}b_{0}&b_{1}&b_{2}\end{bmatrix}\begin{bmatrix}x_{1}\\x_{2}\\x_{3}\end{bmatrix}$

이렇게 나타낸 Controllable Canonical form은 항상 controllable하다는 특징이 있습니다.
즉, Controllable system은 이와 같은 controllable canonical form으로 바꿀 수 있다는 것입니다.
# Controllable Canonical Form 유도

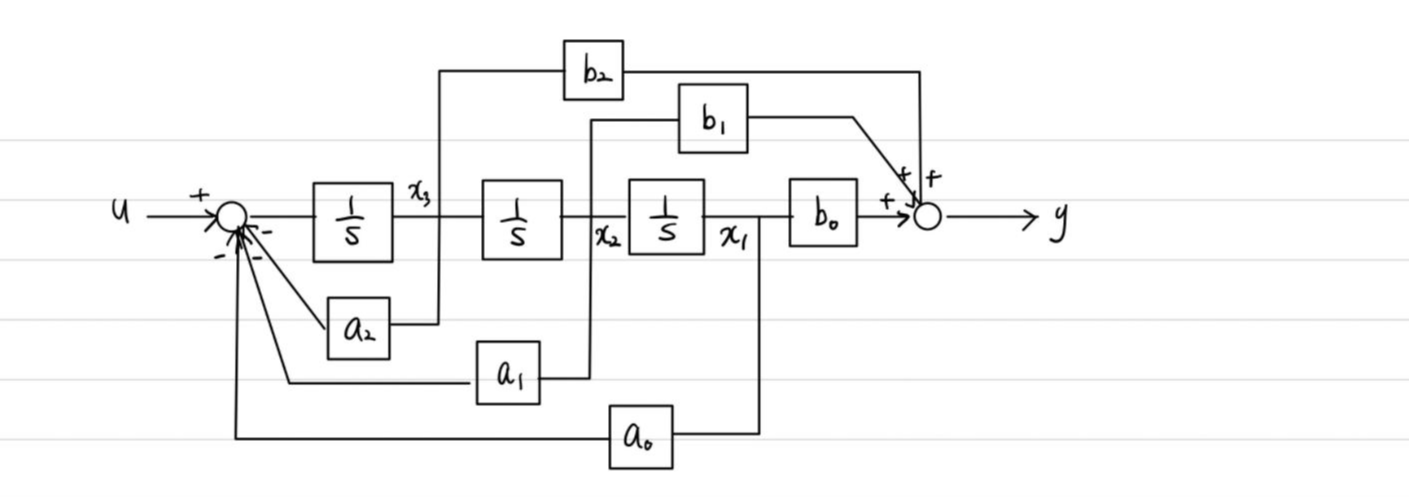
4. Observable Canonical form
Observability 역시 Controllability와 함께 나중에 다룰 것입니다.
간단하게 말하면, observability는 어떤 시스템에서 state를 estimate할 수 있는지에 대한 여부를 말합니다. 시스템에 센서가 있다면 output을 측정할 수 있을 것이고, 이 측정된 결과를 가지고 state를 추정할 수 있는 시스템들이 있습니다. 즉 모든 시스템이 observable한 것은 아닙니다.
Transfer function이 $G(s)=\frac{B(s)}{A(s)}=\frac{b_{2}s^{2}+b_{1}s+b_{0}}{s^{3}+a_{2}s^{2}+a_{1}s+a_{0}}$일 때,
Observable Canonical form은 다음과 같습니다.
$\frac{d}{dt}\begin{bmatrix}x_{1}\\x_{2}\\x_{3}\end{bmatrix}=\begin{bmatrix}-a_{2}&1&0\\-a_{1}&0&1\\-a_{0}&0&0\end{bmatrix}x+\begin{bmatrix}b_{2}\\b_{1}\\b_{0}\end{bmatrix}u$
$y=\begin{bmatrix}1&0&0\end{bmatrix}\begin{bmatrix}x_{1}\\x_{2}\\x_{3}\end{bmatrix}$

observable canonical form은 항상 observable합니다.
# Observable Canonical Form 유도

Controllable Canonical form과 달리 block diagram을 그린 다음에 각 변수를 x1, x2, x3로 설정합니다.
정한 state들을 가지고 식을 세워주면 됩니다.
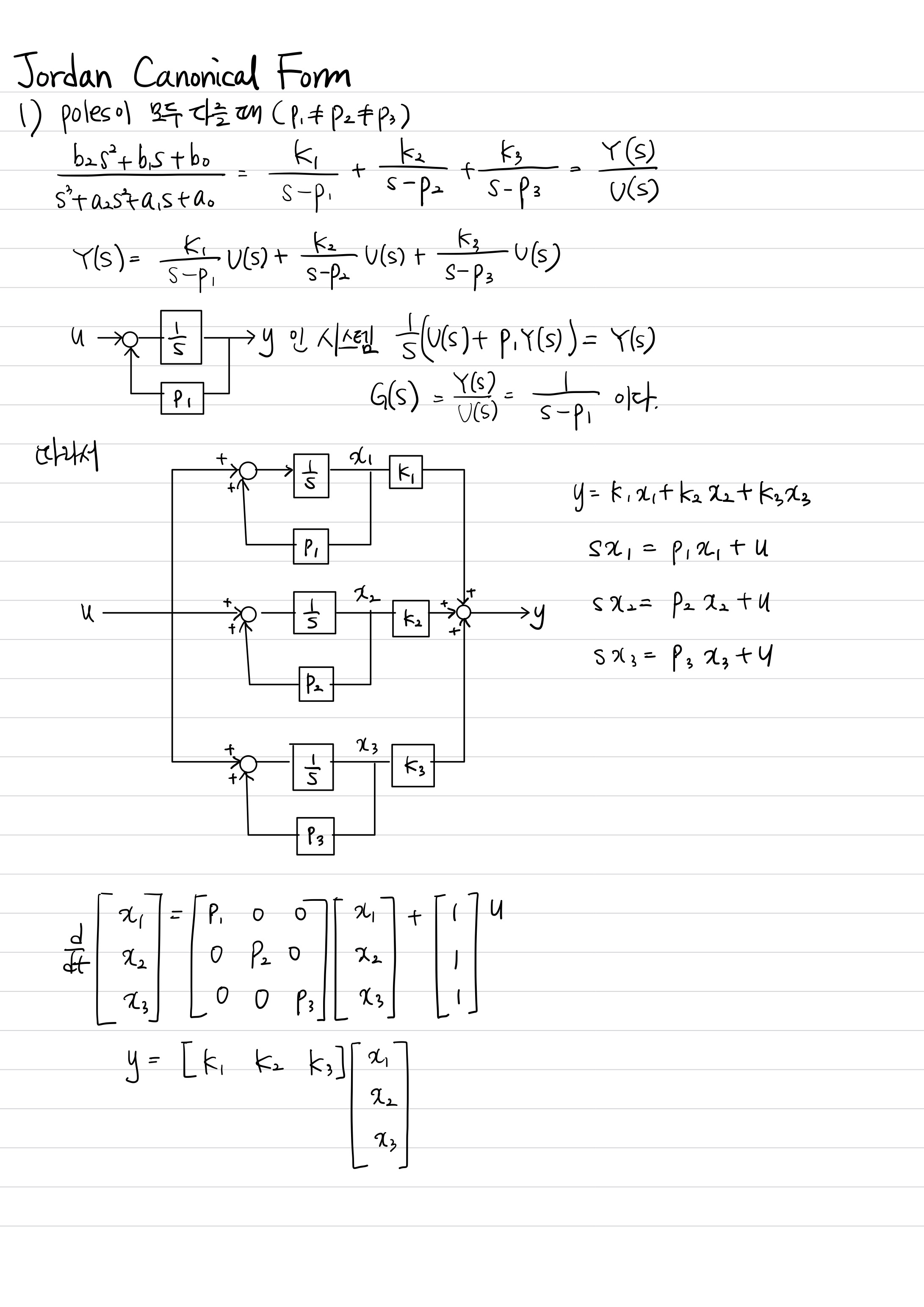
5. Jordan (Diagonal) Canonical Form
마지막으로 볼 State space model은 Jordan Canonical form입니다.
$G(s)=\frac{B(s)}{A(s)}=\frac{b_{2}s^{2}+b_{1}s+b_{0}}{s^{3}+a_{2}s^{2}+a_{1}s+a_{0}}$
다음과 같은 transfer function에서 분모는 characteristic equation이고, 이 characteristic equation을 0으로 만드는 값을 pole이라고 한다고 위에서 설명했습니다.
이 poles를 $p_{1}, p_{2}, p_{3}$라고 한다면,
$s^{3}+a_{2}s^{2}+a_{1}s+a_{0}=(s-p_{1})(s-p_{2})(s-p_{3})$
$\frac{b_{2}s^{2}+b_{1}s+b_{0}}{s^{3}+a_{2}s^{2}+a_{1}s+a_{0}}=\frac{K_{1}}{s-p_{1}}+\frac{K_{2}}{s-p_{2}}+\frac{K_{3}}{s-p_{3}}$
아래는 Jordan Canonical form을 유도하는 방법입니다. (tistory 글로 쓰기에는 너무 방대해서 노트필기로 대체합니다.)
각각 poles이 다를 때, pole에 중근이 있을 때, 복소수 pole일 때 각각을 나눠서 유도합니다.



+ 추가적인 내용
1. determinant of matrix와 adjoint matrix
state space model을 transfer function으로 바꾸는 첫 번째 항목에서 A(s)와 B(s)를 따로따로 구할 수 있습니다.
(나중에 작성)
# 마지막으로 생각해볼 거리
1. state space와 transfer function 사이의 관계
우리는 transfer function와 state space 사이의 전환을 살펴보았습니다. 단순해보이는 transfer function을 block diagram으로 나타내면 복잡하다는 것을 확인해볼 수도 있었습니다. 즉, 비교적 복잡한 형태의 transfer function은 적분기, 피드백, gain 등의 조합으로 나타나며, 사실 이것은 그 dynamics를 보여주는 것으로 보입니다. 우리가 state space model을 만든 이유는 결국 dynamic system을 수학적으로 모델링한 것이며, 이 state space model을 간단한 입출력 간의 관계로 나타낸 것이 transfer function입니다.
2. controllability와 obserbility는 무슨 의미인가? 그리고 왜 중요한가?
이 내용은 다음에 다루도록 하겠습니다.
'연구 Research > 제어 Control' 카테고리의 다른 글
| [고등자동제어] 제어에서 필요한 수학 개념 (0) | 2020.12.07 |
|---|---|
| [고등자동제어] System modeling (2) | 2020.12.03 |
| [고등자동제어] State space model (0) | 2020.11.18 |
| [고등자동제어] Z-transform (0) | 2020.11.17 |
| [고등자동제어] Laplace Transform (0) | 2020.11.13 |
