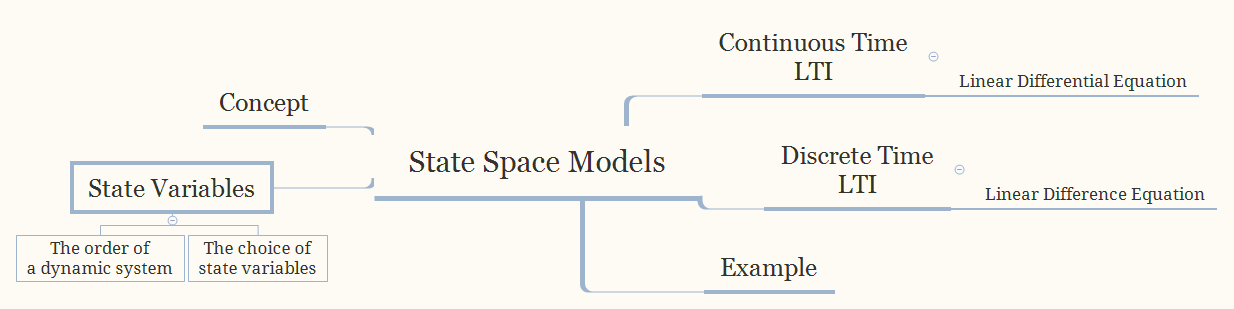
이번에는 제어에서 중요한 주제인 State space model에 대해서 이야기하고자 합니다.
앞서 배웠던 Laplace transform과 Z-transform을 통해서 input과 output간의 관계식을 구할 수 있고, 이를 보통 transfer function이라고 합니다.
예를 들면,

다음과 같은 mass spring damper system이 있다고 합시다. spring의 탄성게수를 k라고 하고, 관성과 질량을 무시하겠습니다. damper는 linear damping이고 damping coefficient는 c로 가정하겠습니다. 이렇게 했을 때, mass에 f(t)라는 힘을 가하고 있습니다.
이 경우에 Differential equation을 적으면 다음과 같습니다. input은 f(t)이고, output은 x(t), 즉 mass의 position입니다.
간단하게 하기 위해 초기조건은 모두 0.
$ m\frac{\ddot{dx}}{dt}+c\frac{\dot{dx}}{dt}+kx = f(t)$
이것을 Laplace transform하면,
$(ms^{2}+cs+k)X(s) = F(s)$
$\frac{X(s)}{F(s)} = \frac{1}{ms^{2}+cs+k}$
다음과 같은 결과가 나옵니다. 들어간 input에 대하여 결과인 output의 비율을 나타낸 것이 transfer function이고, laplace transform된 결과로 표현되기 때문에 문자 s에 대한 식으로 나타납니다.
여튼, 이런 transfer function은 classical한 제어 접근으로서 input과 output의 관계는 쉽게 알 수 있지만, 구체적인 시스템의 작동방식은 파악하기 어렵습니다. 이런 점에서 유용한 것인 state space model입니다.
1. Concept
1) state of Dynamic systems란 무엇인가?
state는 dynamic system이 각 시간마다 가지고 있는 information이자 memory입니다.
어떤 순간에 state에 대해 알고 있고, input을 알고 있다면, state에는 미래에 대한 정보가 있기 때문에 미래를 예측할 수 있습니다.
2. State Variables
Dynamic system의 order는 state variable의 수와 일치합니다. state variable의 수는 system을 필요충분하게 설명할 수 있는 변수의 수를 말합니다.
하지만, state variable의 갯수는 정해져있는데 반해 시스템을 모델링할 때 선택할 수 있는 state variable의 조합은 무한히 많습니다. 이는 예시를 보면서 더 자세히 설명할 것입니다.
3. Discrete Time LTI State space description

Discrete time에서 domain(정의역)은 정수입니다.Discrete time LTI system은 이전에 Linear Difference Equation으로 표현될 수 있다고 했습니다. (z-transform에서)State space model은 어떻게 나타낼 수 있을까요?
(*r,m,n은 모두 임의의 자연수입니다.)
$\text{Input vector : }u(k) = [u_{1}(k), u_{2}(k), ..., u_{r}(k)]^{T} \in U \subset \Re^{r}$
$\text{Output vector :}y(k) = [y_{1}(k), y_{2}(k), ..., y_{m}(k)]^{T} \in Y \subset \Re^{m}$
$\text{State vector : }x(k) = [x_{1}(k), x_{2}(k), ..., x_{n}(k)]^{T} \in X \subset \Re^{n}$
input vector는 r차원 벡터, output vector는 m차원 벡터, state vector는 n차원 벡터입니다.그리고 state space model은 다음과 같습니다.
$ x(k+1) = Ax(k) + Bu(k)$
$ y(k) = Cx(k) + Du(k)$
이 때, input vector, output vector, state vector의 차원이 다르기 때문에 A,B,C,D의 차원이 저마다 다릅니다.
$\text{State Equation : }A \in \Re^{n\times n}, B\in\Re^{n\times r}$
$\text{Output Equation : }C\in\Re^{m\times n}, D\in\Re^{m\times r}$
이 A,B,C,D matrix는 시스템에 따라 고정되는 값입니다.
4. Continuous Time LTI State space description
Continuous time 일 때도 거의 동일합니다.

다음과 같은 시스템일 때 각각의 벡터는 다음과 같습니다.
$\text{Input vector : }u(t) = [u_{1}(t), u_{2}(t), ..., u_{r}(t)]^{T} \in U \subset \Re^{r}$
$\text{Output vector :}y(t) = [y_{1}(t), y_{2}(t), ..., y_{m}(t)]^{T} \in Y \subset \Re^{m}$
$\text{State vector : }x(t) = [x_{1}(t), x_{2}(t), ..., x_{n}(t)]^{T} \in X \subset \Re^{n}$
state space model의 형태는,
$ \frac{dx(t)}{dt} = Ax(t) + Bu(t)$
$ y(t) = Cx(t) + Du(t)$
차원은 위와 동일합니다.
$\text{State Equation : }A \in \Re^{n\times n}, B\in\Re^{n\times r}$
$\text{Output Equation : }C\in\Re^{m\times n}, D\in\Re^{m\times r}$
이 state space model을 수학적으로 방법에 대해서는 추후에 문서를 다시 쓰던가, 이 문서에 덧붙일 예정입니다.
아래는 state space model을 block diagram으로 나타낸 것입니다.
D matrix를 주목해보자면, D가 0이 아닐 때, Input이 시스템을 거치지 않고 직접적으로 output에 영향을 준다고 볼 수 있습니다.
그런데 일반적인 경우에는 input이 output에 직접 영향을 미치는 경우가 없어서 대부분의 경우 D가 0이었습니다. (혹시 D가 0이 아닌 경우를 보게 된다면 수정하겠습니다..ㅎㅎ)

5. example

이 mass spring damper 시스템에서 output은 M의 position이라고 하겠습니다.
즉, p(t)가 시간에 따른 M의 position이라고 할 때,
$\text{Output vector : } y(t)=p(t) \in \Re$
state vector는 제가 임의로
$\text{State vector : }x(t) = \begin{bmatrix} p(t)\\v(t)\end{bmatrix} \in \Re^{2}$
라고 정하겠습니다.
$\text{Input vector : }u(t)=f(t) \in \Re$
위 system의 Differential Equation(DE)는
$M\ddot{y}+B\dot{y}+Ky=u$
$\ddot{y}=\ddot{p}=\dot{v}=-\frac{B}{M}\dot{p}-\frac{K}{M}p+\frac{1}{M}u$
$\frac{d}{dt}\begin{bmatrix}p(t)\\v(t)\end{bmatrix}=\begin{bmatrix}v(t)\\ \dot{v}(t)\end{bmatrix}=\begin{bmatrix}0&1\\-\frac{K}{M}&-\frac{B}{M}\end{bmatrix}\begin{bmatrix}p(t)\\v(t)\end{bmatrix}+\begin{bmatrix}0\\ \frac{1}{M}\end{bmatrix}u(t)$
$y(t)=\begin{bmatrix}1&0\end{bmatrix} \begin{bmatrix}p(t)\\v(t)\end{bmatrix}$
따라서
$A =\begin{bmatrix}0&1\\-\frac{K}{M}&-\frac{B}{M}\end{bmatrix} \in \Re^{2\times2}$
$B =\begin{bmatrix}0\\ \frac{1}{M}\end{bmatrix} \in \Re^{2\times1}$
$C =\begin{bmatrix}1&0\end{bmatrix} \in \Re^{1\times2}$
$D = 0$
state는 다양한 방식으로 만들 수 있습니다. $[p(t), v(t)+p(t)]^{T}$로 선택할 수도 있었습니다.
p(t)와 v(t)의 linear combination은 무한히 많습니다. 즉, state vector로 고를 수 있는 state variables의 조합은 무한히 많습니다.
하지만 이 시스템의 state variables의 갯수는 정해져있습니다.
이를 가지고 A,B,C,D를 구하면 위의 값과 다를 수는 있지만 결론적으로 transfer function은 같을 것입니다.
'연구 Research > 제어 Control' 카테고리의 다른 글
| [고등자동제어] System modeling (2) | 2020.12.03 |
|---|---|
| [고등자동제어] State space와 transfer function의 관계 (2) | 2020.11.19 |
| [고등자동제어] Z-transform (0) | 2020.11.17 |
| [고등자동제어] Laplace Transform (0) | 2020.11.13 |
| [고등자동제어] Introduction (2) | 2020.11.12 |