이번에는 system을 modeling하는 방법에 대해서 알아보려고 합니다.
state space model이나 transfer function을 다루기 이전에 알아야할 내용인 것 같습니다만, 기초적인 제어 내용을 알고 있다는 전제 하에 내용을 정리하다보니 이렇게 되는 것 같습니다.

시스템에는 각 element에 따라 differential equation을 구할 수 있습니다.
그런데 같은 differential equation이라 해도 state variables를 무엇으로 잡는지에 따라 state space model이 달라집니다.
우리의 목표는, 여러 elements가 있는 시스템에서 일관되게 모델링하는 방법을 찾는 것입니다.
그러기 위해서는 시스템에 있는 각 element들의 특성을 이해하는 것이 필요합니다.
1. Engineering system
Engineering system은 다양한 elements들로 구성되어 variables간에 상호작용하면서 input이 들어갈 때 output이 나오는 법칙을 말합니다. Engineering system이나 Energetic system은 비슷하지만, energetic system은 시스템을 power나 energy의 입출에 좀 더 중점을 둔 표현이라고 생각합니다. Energetic system에는 mechanical, electrical, fluid, thermal system 등이 있습니다.
우리가 system에서 볼 elements는 power의 관점에서 분류할 수 있습니다.
그래서 다음 내용에 들어가기 전에 power가 무엇인지 개념을 잡고 가야합니다.
# Power
power P는 the rate of work or energy입니다. 고등학교 물리에서 work와 energy가 서로 전환될 수 있음을 배웠기 때문에 work or energy라고 표현했습니다. 예를 들어 상자를 경사로에 밀어올려, 즉 일을 해서 위치에너지를 증가시키는 것처럼요.
또한 power의 단위 중 하나인 W(와트)는 J/s이고 시간 당 에너지를 뜻합니다.
한 energetic system에서 여러 Power가 들어온다고 생각해보면,
$\sum_{k=1}^{n}P_{k}(t)=\frac{d}{dt}E(t)+P_{D}$
$P_{k}(t)$ : k번째 energy port에서 system으로 들어오는 power
$E(t)$ : system에 저장되는 에너지
$P_{D}(t)$ : system에서 소멸(dissipate)되는 에너지
시스템의 종류에 따라 power를 나타내는 공식은 다를 수 있습니다.
mechanical system에서는 $P_{mech}=\text{velocity}\times\text{force}$
electrical system에서는 $P_{elec}=\text{voltage}\times\text{current}$
fluid system에서는 $P_{fluid}=\text{pressure}\times\text{Volumetric flow rate}$
2. Variables
이제 variables에 대해서 공부할 것입니다. elements를 이해하기 위해 또 필요한 내용이 variable입니다.
1) Through Variables

여기 translational spring이 있습니다. 우리는 특별한 조건이 있지 않는 이상 spring을 mass가 없다고 가정합니다. 이럴 때 이 spring에 걸리는 힘 F는 스프링 양끝 모두 같습니다. 만약 양끝에 걸리는 힘이 다르면 net force가 0이 아니고 질량은 0이므로 가속도가 무한으로 발산합니다.(F=ma)
이렇게 external force is transmitted through the spring이므로, force F는 Through variable이라고 합니다.
즉 through variable은 element을 통해(through) 흐르는 변수를 말합니다. 균일하게 흐르기 때문에 element의 양 끝에서 동일한 값을 가집니다. 예를 들어 electrical system에서 전류가 흐를 때 양 쪽 모두 같습니다.
2) Across Variables
위의 예를 이어서 보겠습니다. 스프링이 힘을 받는다면 스프링 양끝의 움직임은 다를 것입니다. 스프링은 늘어났다 줄어들었다하면서 운동을 하니까요. 즉 스프링은 속도가 존재합니다. 스프링의 속도를 잰다면 x1 지점의 속도와 x2 지점의 속도의 차이를 구하면 됩니다.
velocity difference is measured across the spring element이므로, velocity v는 Across variable입니다.
across variable은 element 사이(across)의 차이로 나타나는 변수를 말합니다. voltage도 across variable 중 하나인데 voltage는 절대적인 값이라기 보다면 특정 지점(보통 ground)보다 얼마나 더 높은지 비교해서 구할 수 있는 값입니다. velocity는 inertial frame에서 얼마나 더 빠른지 나타내는 값입니다.
아래의 표는 각 energetic system의 through variable과 across variable를 정리한 표입니다.
Integrated through variable과 Integrated across variable도 나와있습니다. force를 적분하면 momentum(또는 impulse)이고, velocity를 적분하면 displacement가 나오기 때문에 쉽게 납득하실 수 있을 것입니다.

3. Elements
Variable을 배웠으면, 이제 power와 variable을 이용해 elements를 분류하겠습니다.
1) T-element ; Inductive storage
T-element는 Through variable로 power를 저장하는 element입니다.
electrical system에서는 Inductor(L), mechanical system에서는 Spring(k)가 T-element가 됩니다. (왜 그런지는 뒤에서 자세히 설명하겠습니다.)
아래는 T-element를 differential equation으로 나타낼 때의 식, 그리고 에너지를 element에 대해 나타낸 것입니다.

맨 왼쪽 열을 보면, across variable을 through variable의 미분으로 표현할 수 있다는 것을 알 수 있습니다.
또한 이 element가 가지고 있는 energy는 through variable로 표현할 수 있습니다. 즉, through variable로 power를 저장한다는 것을 살펴볼 수 있습니다.
2) A-element ; Capacitive storage
T-element와 비슷하게 A-element는 Across variable로 power를 저장하는 element입니다.
electrical system에서는 capacitor(C), mechanical system에서는 mass(M)가 A-element 역할을 합니다.
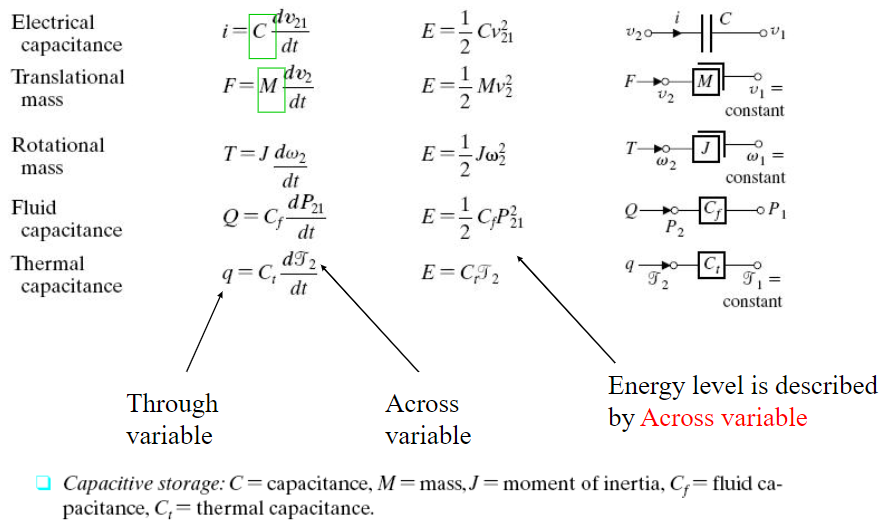
위 그림을 보면 through variable이 across variable의 미분(방정식)으로 나타낼 수 있음을 알 수 있습니다. 또한 에너지는 across variable로 표현할 수 있으므로, A-element는 across variable로 power를 저장하는 element이라고 파악하면 됩니다.
3) D-element ; Energy dissipator
D-element는 T-element나 A-element와 달리 에너지를 저장하지 않고 에너지를 dissipate하는 element입니다.
electrical system에서는 resistor(R), mechanical system에서는 damper가 D-element입니다.

위에서 through variable과 across variable이 미분(방정식) 관계인 것과 달리, D-element는 algebraic equation으로 표현됨을 알 수 있습니다.
4) Element를 통해 알 수 있는 것
element를 파악하는 것은 시스템을 이해하는 데에 도움이 됩니다. 결국 이 과정들은 시스템을 잘 모델링하기 위한 것이니까요.
A-element와 T-element는 위에서 본 것과 같이 through variable과 across variable의 미분(방정식) 관계로 나타낼 수 있음을 알았습니다. 따라서 A-element와 T-element의 갯수를 알면, 이 개수는 곧 시스템의 differential equation의 갯수라고 생각할 수 있습니다. 각 element마다 differential equation을 하나씩 가지고 있기 때문입니다. D-element는 미분(방정식) 관계가 아니므로 differential equation의 갯수에는 영향을 미치지 않습니다.

다음과 같은 시스템이 있다면, A-element인 mass가 1개, T-element인 spring이 1개 있으므로 2개의 DE가 나올 수 있음을 미리 식을 세우기 전에 파악할 수 있습니다.
또한 Through variable과 Across variable을 state variable로 채택함으로써 일관된 방식으로 시스템을 모델링할 수 있습니다. 이것에 대한 예시는 아래에서 다루겠습니다.
4. Mechanical system

mechanical system은 위의 그림에서 알 수 있듯이, Passive element와 Active element로 구분하고 그 하위에 또 element가 존재합니다. Active element에는 source가 있는데 source는 power를 generate하는 역할을 합니다.
우리가 주목할 부분은 passive element입니다.
각 element마다 power를 어떻게 저장하는지 유도해볼 것입니다.
1) D-element (Damper)

D-element인 damper에 대하여 dissipated power를 구할 수 있습니다.
$F_{d}=Bv_{d}$는 damper가 linear damper라고 가정하고 쓴 식이며, non-linear하게 표현할 수도 있습니다. 그것이 실제와 더 가깝기도 합니다. 하지만 지금 이 글에서는 다 linear하게 가정합니다.
2) A-element (Mass)

회색으로 줄이 쳐진 부분만 집중하셔도 됩니다.
mass에서 through variable과 across variable 간의 관계식을 구하고, 이 관계식을 이용해 에너지 식을 유도하는 과정입니다.
3) T-element (Spring)

마찬가지로 spring에서의 through variable과 across variable의 관계식을 구하고, 에너지 식을 유도해냅니다.
보통 spring에 저장되는 (탄성)에너지는 $\frac{1}{2}kx_{s}^{2}$이라고 하지만, $x_{s}$는 across variable도, through variable도 아니기 때문에 에너지를 표현하는데에 적절하지 않습니다. $\frac{1}{2k}F_{s}^{2}(t)$와 같이 through variable에 관한 식으로 표현할 수 있습니다.
4) Mechanical variables의 관계
앞서 element들을 볼 때, through variable, across variable, 그리고 더 나아가 integrated through variable, integrated across variable의 관계를 살펴볼 수 있습니다.

force : through variable
impulse : integrated through variable
velocity : across variable
displacement : integrated across variable
이 각각의 변수들이 linear하게 연결될 수 있는 element들은 위에 써진 바와 같다.
force-velocity는 damper, impulse-velocity는 mass, displacement-force는 spring으로 algebraic equation으로 연결되어있다.
impulse와 displacement가 각각 through variable, across variable의 적분된 값이기 때문에 mass와 spring은 through variable과 across variable의 미분방정식으로 나타낼 수 있는 것이다.
5. Electrical system

1) D-element (Resistor)

2) A-element (Capacitor)

3) T-element (Inductor)

# Flux linkage
여기서 나오는 Flux linkage에 관해 잠시 짚고 넘어가겠습니다. 저는 이 단어를 처음 접했거든요.
위에서는 Flux linakage를 문자 P로 표현했지만 좀 더 일반적으로는 $\lambda$를 씁니다.
정의 상 voltage의 time integral $\int \varepsilon dt\text{, where }\varepsilon\text{ is voltage}$로 표현이 되며, 거꾸로 말하면 voltage는 Flux linkage의 시간변화율과 같다는 것을 의미합니다.
추가적인 내용은
en.wikipedia.org/wiki/Flux_linkage
4) Electrical element의 관계

mechanical variables와 마찬가지로, through variable, across variable과 그 변수들을 이어줄 수 있는 element들을 중심으로 생각해볼 수 있습니다.
5) Active element
위에서 다룬 element는 모두 passive element의 경우입니다. 그러나 electrical element 중에서도 active element가 존재합니다.
battery와 같은 voltage source는 source 중에서도 A-source라고 불리며, across variable인 voltage를 공급합니다. 따라서 voltage는 고정이 되고 저항에 따라 흐르는 전류가 달라집니다.
일정 전류를 흘려보내주는 current source는 T-source라고 불리며, through variable인 current를 회로에 공급합니다. current가 고정이기 때문에 저항에 따라 다른 element에 걸리는 전압이 정해집니다.
6. Fluid system
(나중에 시간이 나면 정리하는 걸로... 내용 상에 critical한 부분은 아니기 때문)
7. Example
'연구 Research > 제어 Control' 카테고리의 다른 글
| [고등자동제어] LTI 시스템의 state equation 풀기 (1) (0) | 2020.12.15 |
|---|---|
| [고등자동제어] 제어에서 필요한 수학 개념 (0) | 2020.12.07 |
| [고등자동제어] State space와 transfer function의 관계 (2) | 2020.11.19 |
| [고등자동제어] State space model (0) | 2020.11.18 |
| [고등자동제어] Z-transform (0) | 2020.11.17 |