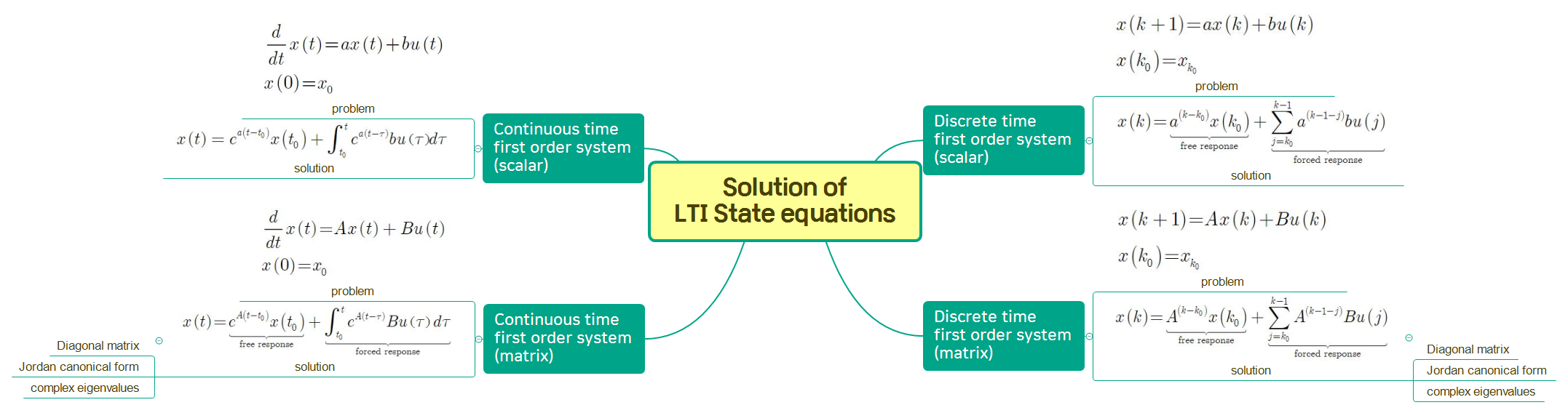
앞서 본 State space model을 식으로써 풀어볼 수 있습니다.
일반적인 미분방정식은 풀 수 있다면, 그것을 확장하여 행렬로 이루어진 미분방정식도 풀 수 있습니다. 그래서 처음에는 스칼라 계수를 가진 미분방정식을 풀고 이것을 행렬로 확장할 것입니다.
1. Continuous time first order system (scalar)
시스템에서 continuous time first order system은,
$\frac{dx(t)}{dt}=ax(t)+bu(t)$
$x(t_{0})=x_{0}$
다음과 같이 주어져있습니다.
이 시스템은 linear하기 때문에 $\frac{dx(t)}{dt}=ax(t)+bu(t)$와 $\frac{dx(t)}{dt}=ax(t)$의 solution의 조합으로 표현할 수 있습니다.
$\frac{dx(t)}{dt}=ax(t)$ : 이와 같이 input이 없이 시스템의 solution을 구하면, 그 solution을 free response라고 합니다.
또한 $u(t)$는 시스템에 들어가는 입력(input)이므로, $\frac{dx(t)}{dt}=ax(t)+bu(t)$의 solution은 free response와 forced response의 조합으로 나타날 수 있습니다.
1) free response
$\dot{x}=ax, x(t_{0})=x_{0} \rightarrow x(t)=e^{a(t-t_{0})}x_{0}$
이 solution은 대입을 통해서 알아낼 수 있습니다. $e^{at}$를 미분방정식에 대입하면,
$\dot{x}=ae^{at}=ax(t)$
이고 따라서 $e^{at}$가 solution이 됩니다.
그런데, 조건이 주어져있으므로 $x(t_{0})=x_{0}$ 조건을 대입하면 최종 결과를 얻을 수 있습니다.
# free response의 경향성
지금 구한 free response는 $x(t)=e^{at}x(0)$ (초기조건이 주어졌을 때)
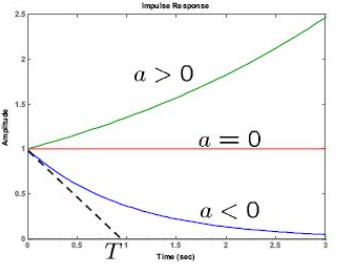
a가 0보다 크면 발산하고, a=0이면 초기조건에서 그대로 유지, a가 0보다 작으면 0으로 수렴합니다. 우리는 stable한 시스템을 주로 다루기 때문에 $a<0$인 케이스를 보겠습니다. 이 때, free response의 Time constant를 정의하는데, time constant는 x(t)가 초기값의 37%(=$e^{-1}$=약 0.37로 될 때까지의 시간을 말합니다.
따라서 $\text{Time constant }T=\frac{1}{|a|}$입니다. 절댓값을 씌우는 이유는 $a<0$인 것이 전제이기 때문입니다.
2) forced response
다음으로 $\frac{dx(t)}{dt}=ax(t)+bu(t), x(t_{0})=x_{0} \rightarrow x(t)=e^{a(t-t_{0}}x(t_{0})+\int_{t_{0}}^{t}e^{a(t-\tau)}bu(\tau)d\tau$
이 solution을 구하는 방법은
$\dot{x}(t)-ax(t)=bu(t)$ 로 식을 변형한 다음, 양변에 $e^{-at}$
$e^{-at}\dot{x}-e^{-at}ax=\frac{d}{dt}(e^{-at}x(t))=e^{-at}bu(t)$
이제 양변을 적분하겠습니다.
$\int_{0}^{t}e^{-a\tau}x(\tau)d\tau=e^{-at}x(t)-x(0)=\int_{0}^{t}e^{-a\tau}bu(\tau)d\tau$
$x(t)=e^{at}x(0)+\int_{0}^{t}e^{a(t-\tau)}bu(\tau)d\tau$ (initial condition이 있을 때)
적분구간만 $\int_{t_{0}}^{t}$라면 forced response의 시작부분에 언급한 solution과 동일하게 나옵니다.
* 마지막으로 확인을 위해 Leibniz's Theorem을 이용해 solution이 미분방정식을 만족하는지 알 수 있습니다.
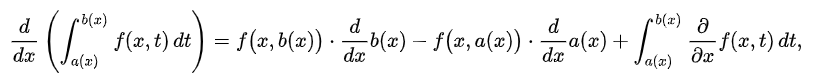
위 식의 출처 : en.wikipedia.org/wiki/Leibniz_integral_rule
Leibniz integral rule - Wikipedia
From Wikipedia, the free encyclopedia Jump to navigation Jump to search This article is about the integral rule. For the convergence test of alternating series, see Alternating series test. Differentiation under the integral sign formula In calculus, Leibn
en.wikipedia.org
$x(t)=e^{a(t-t_{0})}x(t_{0})+\int_{t_{0}}^{t}e^{a(t-\tau)}bu(\tau)d\tau$ 일 때
$\dot{x}(t)=ax(t)+bu(t)$를 만족하는지 $\dot{x}$에 대입해보겠습니다.
$\frac{dx(t)}{dt}=ae^{a(t-t_{0})}x(t_{0})+\int_{t_{0}}^{t}ae^{a(t-\tau)}bu(\tau)d\tau+e^{a(t-t)}bu(t)=a(e^{a(t-t_{0})}+\int_{t_{0}}^{t}e^{a(t-\tau)}bu(\tau)d\tau)+bu(t)=ax(t)+bu(t)$
적분식을 미분할 때는 위의 Leibniz integral rule을 사용하면 되는데, 위의 문자가 다소 헷갈릴 수 있을 것 같네요. Leibniz integral rule에서 $x$ 대신 $t$라고 생각하고, $t$ 대신 $\tau$라고 생각하면 됩니다.
# forced response의 경향성
unit step forced response를 계산하면 ($\int_{0}^{t} e^{a(t-\tau)}bu(\tau)d\tau=\int_{0}^{t}be^{a(t-\tau)}$)
free response 부분을 제외한다면 $x(t)=\frac{b}{|a|}(1-e^{at})$이 나옵니다.
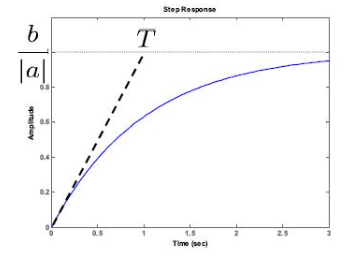
다음을 그래프로 나타내면 $a<0$이라는 전제 하에 다음과 같이 구할 수 있다. 앞서 free response에서 time constant를 구한 것처럼,
$\text{time constant }T=\frac{1}{|a|}$일 때
$x(T)=\frac{b}{|a|}(1-e^{-1})=0.67\frac{b}{|a|}$
2. Continuous time nth order system (matrix)
1) State equation
위의 scalar와 달리 n coupled first order differential equation이 있을 때 matrix의 형태로 state equation을 나타낼 수 있습니다.
# 왜 n개의 first order differential equation이 있는 system을 nth order system이라고 할까?
저는 사실 왜 first order differential equation이 n개 있음에도 불구하고 first order system이 아니라 nth order system이라고 하는지 이해가 되지 않았습니다.
그런데
mathonline.wikidot.com/converting-nth-order-odes-to-systems-of-n-first-order-odes
mathonline.wikidot.com/nth-order-ordinary-differential-equations
이 사이트를 통해 도움을 얻었습니다. 모든 nth order system은 n개의 first order system으로 나타낼 수 있다는 것이 증명되어 있습니다. 따라서 일반적인 시스템이 nth order differential equation으로 나타낼 때, 이것을 state space model로 나타내기 위해 n개의 first order system으로 나타내는 것이었습니다.
당연하게 알고 있으신 분들이 있겠지만, 지금까지 해온 state space model이 수학의 관점에서는 nth order ODE를 n개의 first order ODE로 바꾸는 과정이었다고 연결지어볼 수 있겠네요.
(n개의 first order ODEs에서 nth order ODE로 바꾸려고 하다보니 이상함을 느꼈던 것 같습니다.)
$\frac{d}{dt}x(t)=Ax(t)+Bu(t)$
$x(t_{0})=x_{0}$
$x\in R^{n}, A\in R^{n\times n}$
위의 solution을 참고하여 비슷한 꼴의 solution을 구할 수 있습니다.
$x(t)=e^{A(t-t_{0}}x(t_{0})+\int_{t_{0}}^{t}e^{A(t-\tau)}Bu(\tau)d\tau$
이 식에서 고민해봐야할 부분은, $e^{At}$를 어떻게 구할 것인가 입니다.
2) Matrix exponential
$A\in R^{n\times n}$ 일 때
matrix exponential $e^{At}=I_{n}+At+\frac{1}{2}A^{2}t^{2}+\cdots+\frac{1}{n!}A^{n}t^{n}+\cdots \in R^{n\times n}$
로 나타낼 수 있습니다. 이는 taylor expansion($e^{at}=1+at+\frac{1}{2}a^{2}t^{2}+\cdots+\frac{1}{n!}(at)^{n}+\cdots$)과 유사합니다.
이에 대한 성질도 보여드리자면,
* $(e^{At})^{-1}=e^{A(-t)}$ : t 대신 -t를 집어넣는 것만으로 역행렬을 구할 수 있다.
* $e^{A(t_{1})}e^{A(t_{2})}=e^{A(t_{1}+t_{2})}$
* $e^{A(t)}A = Ae^{A(t)}$ : 둘 다 n by n matrix인데 교환법칙이 성립한다.
* $e^{A(t)}e^{B(t)}=e^{(A+B)(t)}\Longleftrightarrow AB=BA$
3) Solution matrix 계산
Case1 : Diagonal matrix (eigenvalue가 모두 다를 때)
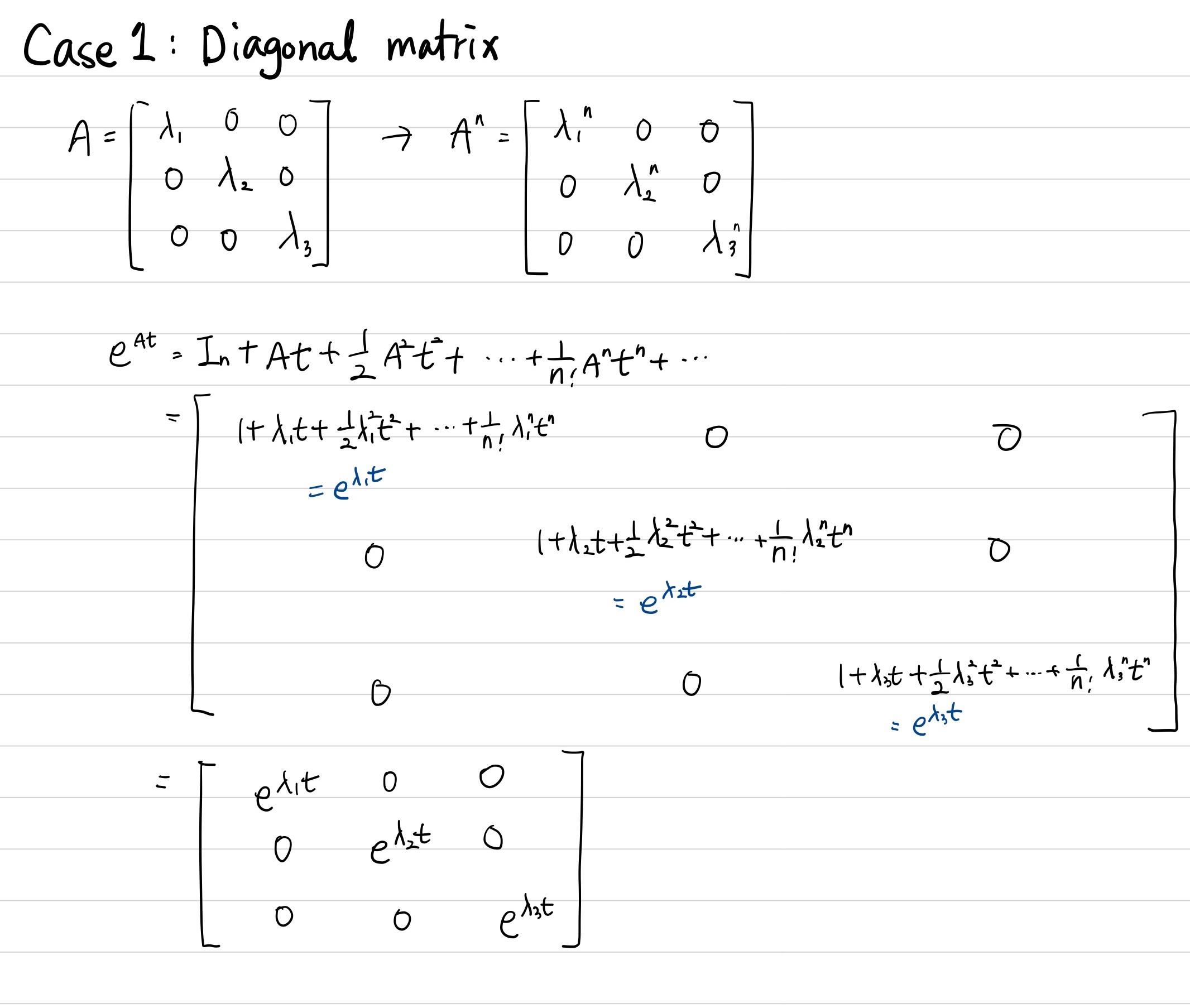
시스템이 안정적이기 위해서는 t가 무한대로갈 때 $e^{At}$가 발산하면 안됩니다. 즉, $\underset{t\rightarrow \infty}{lim}e^{\lambda_{i}t=0}$이어야 합니다. 그 말은 곧 $\text{real}(\lambda_{i})<0$ 이라는 의미입니다.
모든 $\lambda$의 실수부가 음수여야 합니다. 허수부는 진동하는 부분이므로 수렴, 발산 여부에 영향을 주지 않는다.
Case2 : Jordan canonical form (중근이 있을 때)

발산하지 않을 조건
$\underset{t\rightarrow \infty}{lim} t^{m}e^{\lambda_{i}t}=0\Leftrightarrow \text{Real}(\lambda)<0$
Case3 : Complex eigenvalues (복소수근이 존재할 때)

발산하지 않을 조건$\underset{t\rightarrow \infty}{lim}e^{\sigma t}cos(\omega t)=0 \Leftrightarrow \text{Real}(\sigma)<0$
# 생각할 거리
만약 matrix가 jordan form, diagonal matrix, complex eigenvalue의 조합이면 어떻게 할 것인가?
예를 들면
$A=\begin{bmatrix} p_{1} & 0 & 0\\ 0 & p_{m} & 1\\ 0 & 0 & p_{m} \end{bmatrix}$
$A=\begin{bmatrix} p_{1} & 0 & 0\\ 0 & \sigma & \omega\\ 0 & -\omega & \sigma \end{bmatrix}$
일 때 $e^{At}$를 구할 수 있을까?
그래서 해보았습니다. 위에서 증명했던 과정과 동일하게 한 결과입니다.
1) Repeated eigenvalue 2개만 있을 때
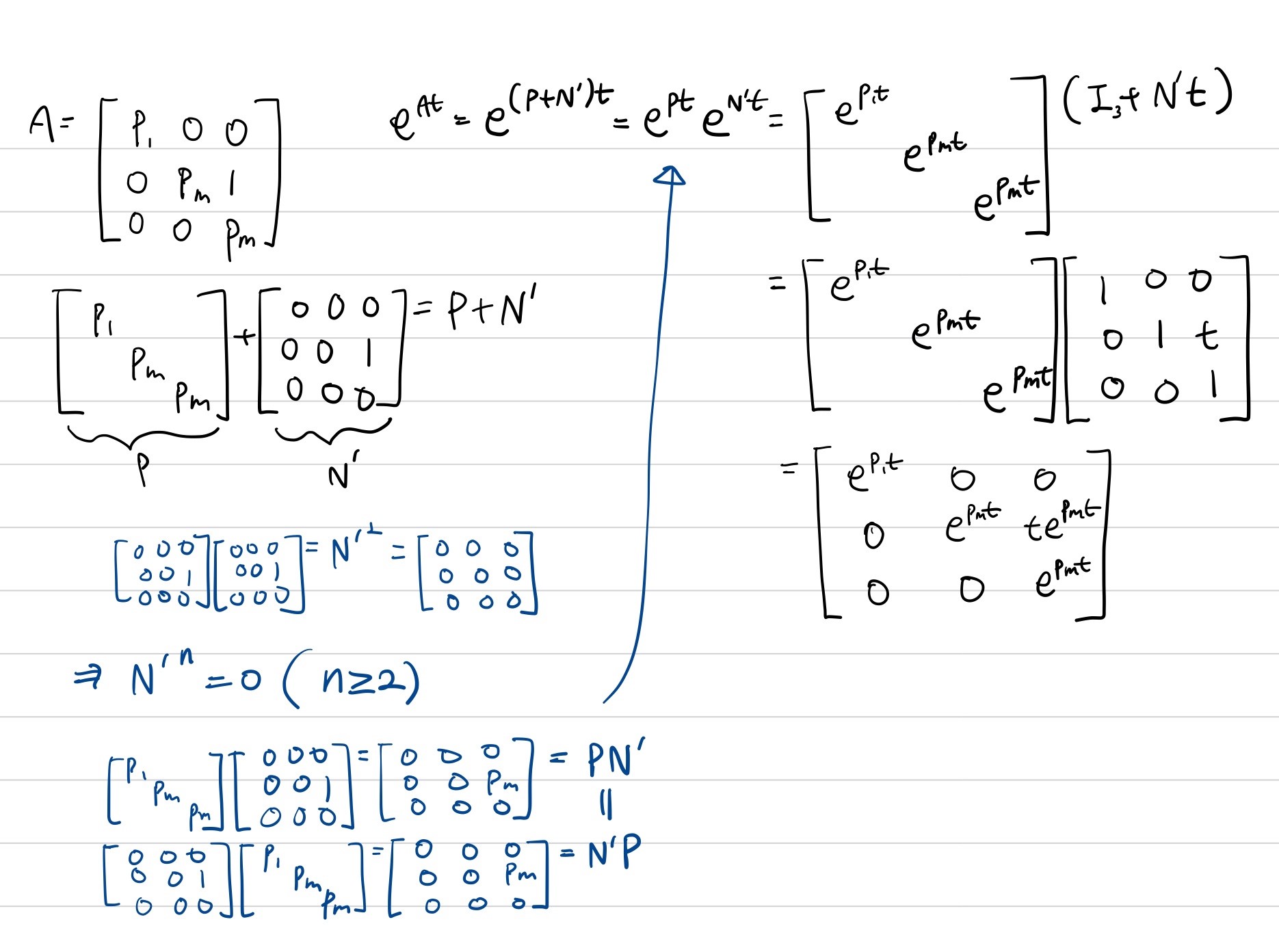
2) complex eigenvalues 외에도 다른 eigenvalue가 있을 때

직접 해보면 단순해서 굳이 해야하나 싶지만, 직접 해보다보면 그 패턴을 발견하기 더 쉬워진다는 장점이 있습니다.
Discrete system part는 (2)에서 이어서 쓰겠습니다.
'연구 Research > 제어 Control' 카테고리의 다른 글
| [고등자동제어] Similarity Transformation for matrix exponential (1) (0) | 2020.12.29 |
|---|---|
| [고등자동제어] LTI 시스템의 state equation 풀기 (2) (0) | 2020.12.16 |
| [고등자동제어] 제어에서 필요한 수학 개념 (0) | 2020.12.07 |
| [고등자동제어] System modeling (2) | 2020.12.03 |
| [고등자동제어] State space와 transfer function의 관계 (2) | 2020.11.19 |