
1. Discrete time first order system (scalar)
$x(k+1)=ax(k)+bu(k)$
$x(k_{0})=x_{k_{0}}$
다음과 같은 시스템의 solution : $x(k)=a^{k-k_{0}}x(k_{0})+\sum_{j=k_{0}}^{k-1}a^{(k-1-j)bu(j)}$
앞서 continuous time에서도 말했듯이 free response와 forced response의 조합으로 구할 수 있다.
2. Discrete time nth order system (matrix)
1) State equation
$x(k+1)=Ax(k)+Bu(k)$
$x(k_{0})=x_{k_{0}}$
$x\in R^{n}, A\in R^{n\times n}$
solution은 $x(k)=A^{k-k_{0}}x(k_{0})+\sum_{j=k_{0}}^{k-1}A^{(k-1-j)}Bu(j)$ 입니다.
$\sum$에서 $A^{k-1-j}Bu(j)$이 왜 이렇게 나오는지에 대해서 짚고 넘어가려고 합니다.
아래 내용은 Lectures on Dynamic Systems and Control이라는 MIT 수업을 참고했습니다.
$x(k+1)=Ax(k)+Bu(k)$
$x(1)=Ax(0)+Bu(0)$
$x(2)=Ax(1)+Bu(1)=A^{2}x(0)+\{A^{1}Bu(0)+A^{0}Bu(1)\}$
$x(3)=Ax(2)+Bu(2)=A^{3}x(0)+\{A^{2}Bu(0)+A^{1}Bu(1)+A^{0}Bu(2)\}$
x(k)에서 k가 증가함에 따라 x(0) 앞에 곱해지는 A는 k제곱만큼 이루어지고, 뒤의 u(k) 역시 패턴을 찾을 수 있습니다.
$\text{generalization : }x(k)=A^{k}x(0)+\sum_{j=0}^{k-1}A^{k-1-j}Bu(j)$
Continuous time에서 그랬던 것처럼 $A^{k}$를 어떻게 구할 것인지 case별로 나누어서 생각해보겠습니다.
Case1 : Diagonal matrix
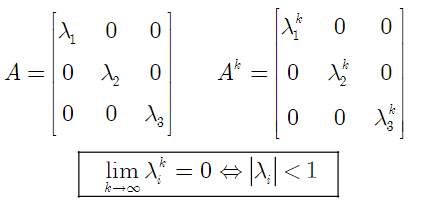
Case2 : Jordan canonical form


Case3 : Complex eigenvalues


'연구 Research > 제어 Control' 카테고리의 다른 글
| [고등자동제어] Similarity Transformation for matrix exponential (2) (0) | 2020.12.29 |
|---|---|
| [고등자동제어] Similarity Transformation for matrix exponential (1) (0) | 2020.12.29 |
| [고등자동제어] LTI 시스템의 state equation 풀기 (1) (0) | 2020.12.15 |
| [고등자동제어] 제어에서 필요한 수학 개념 (0) | 2020.12.07 |
| [고등자동제어] System modeling (2) | 2020.12.03 |