이번에는 dynamics를 통해 제어기를 생각하는 방법에 대해 다룬다.
사실 제어기를 설계하는 것은 정답이 있는 게 아니라 어떻게 모델링해서 어느 부분을 제어할 것이냐에 따라 달라질 수 있다. 따라서 본인이 달성하고자 하는 성능 지표나 운용 목적, 센서의 유무 등을 따져보아야 한다.
dynamics를 알아야 하므로 다음 글을 참고한다.
1. Outer loop - Inner loop
제어기에서는 내부 루프와 외부 루프로 제어기가 구성된다. 내부 루프는 가장 빠른 response를 기준으로 설정이 된다.
가장 기본적으로 위치, 속도, 자세각, 각속도가 측정 가능하다고 가정한다. (그래야 피드백을 할 수 있으니까)
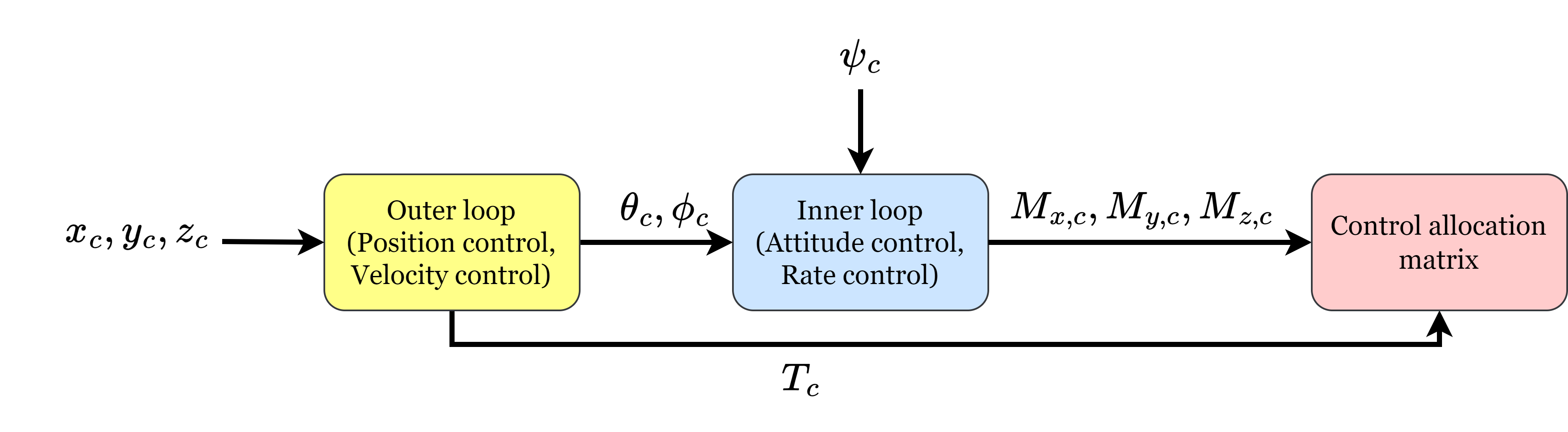
위 그림과 같이 위치 커맨드가 주어질 때의 루프를 나타낸 것이다. 위치가 주어지면, 이를 위한 속도 커맨드를 계산하고, 속도를 내기 위한 롤과 피치각 커맨드를 계산한다. 롤과 피치각, 그리고 주어지는 요각 커맨드를 따라가는 자세각 제어기가 들어간다. 자세각 제어기는 각속도 커맨드를 만들어내며, 각속도 커맨드를 추종하기 위한 각속도 제어기를 만든다.
물론 상황에 따라 속도 커맨드가 주어질 수도 있고, 각도 커맨드가 주어질 수 있다. 그러면 앞선 과정을 생략하고 바로 각도 커맨드를 넣어서 inner loop로 들어가도록 하면 된다.
2. 롤, 피치 자세각 커맨드 생성
위의 내용을 보면 속도 제어기에서 자세각 커맨드를 출력한다고 설명했다. 이 과정은 어떻게 가능한 것일까?
고도를 제어하는 경우든, Z축 속도를 제어하든 관성좌표계(정확히는 Vehicle frame으로 생각해야하지만 러프하게 관성좌표계)에서 고도를 제어하는 과정은 결국 $F_{z}$를 통해서 결정된다. 여기서 $F_{z}$를 관성좌표계 기준에서 z축 힘이지만 이를 만들어내려면 중력을 이겨내는 thrust ($T_{c}$)가 필요하다. 또한 드론은 구조 상 body 기준 $X,Y$ 축으로 힘을 낼 수가 없다. 따라서 관성좌표계에서 속도를 만들어내려면 자세각을 만들어서 $V_{x},V_{y}$를 만들어내야하는 것이다.
이전 글에서의 다음 식을 가져와보자.
\begin{equation}
\left[\begin{array}{c}
\ddot{x} \\
\ddot{y} \\
\ddot{z}
\end{array}\right]=\frac{1}{m}\left[\begin{array}{c}
F_x \\
F_y\\
F_z+g
\end{array}\right]=-\frac{T}{m}\left[\begin{array}{c}
\cos \psi \sin \theta \cos \phi+\sin \phi \sin \psi \\
\sin \psi \sin \theta \cos \phi-\sin \phi \cos \psi \\
\cos \theta \cos \phi
\end{array}\right]+\left[\begin{array}{c}
0 \\
0 \\
g
\end{array}\right]
\end{equation}
$F_{z}=-T\times(\cos \theta \cos\phi) +mg$
이기 때문에 $T_{c}=-m\dfrac{a_{z,c}-g}{ \cos\theta \cos\phi }$으로 계산이 된다.
$a_{z,c}$는 제어기 계산을 통해 구한 feedback 값이다. ($F_{z,c}=ma_{z,c}$)
이제 $X,Y$ 루프에서 자세각을 변환하는 방법을 알아보자.
제어루프를 통해 얻을 수 있는 것은 관성좌표계 기준 $a_{x,c}, a_{y,c}$를 얻게 될 것이다.
위 식에서 롤,피치 자세각이 작다고 가정할 때
$$\begin{bmatrix} \ddot{x} \\ \ddot{y} \end{bmatrix}= \begin{bmatrix} \cos \psi \sin \theta \cos \phi+\sin \phi \sin \psi \\
\sin \psi \sin \theta \cos \phi-\sin \phi \cos \psi \end{bmatrix} =\dfrac{T}{m}\begin{bmatrix} \sin\psi & \cos\psi \\ -\cos\psi & \sin\psi \end{bmatrix} \begin{bmatrix} \phi \\ \theta \end{bmatrix}$$
따라서 $a_{x,c}, a_{y,c}$가 계산될 경우
$$ \begin{bmatrix} \phi_{c} \\ \theta_{c} \end{bmatrix} = \dfrac{m}{T} \begin{bmatrix} \sin\psi & -\cos\psi \\ \cos\psi & \sin\psi \end{bmatrix} \begin{bmatrix}a_{x,c} \\ a_{y,c}\end{bmatrix} $$
로 필요한 자세각을 계산할 수 있다.
여기서 $T$를 알아야한다는 문제가 있으므로 이를 처리하는 방식에는 여러가지가 존재한다.
그리고 모멘트 계산의 경우에는 코리올리 텀을 무시한 간단한 dynamics를 사용하는 편이다.
$$\begin{aligned}\dot{p} &= \dfrac{M_{x}}{I_{xx}} \\ \dot{q} &= \dfrac{M_{y}}{I_{yy}} \\ \dot{r} &= \dfrac{M_{z}}{I_{zz}} \end{aligned}$$
참고) 다른 방식
다른 문헌[1]을 찾아보니 dynamics를 이와 같이 풀지 않고 관성좌표계(주로 NED 좌표계)에서 헤딩각($\psi$)만큼 변환한 XYD 좌표계를 사용하여 dynamics를 만들고 이를 기준으로 롤, 피치 각을 생성하는 경우도 존재했다.
이렇게 할 경우에는 dynamics를 다음과 같이 간소화하였다.
$$\begin{aligned} \ddot{x} &= -\cos\phi \sin\theta \dfrac{T}{m} \\ \ddot{y} &= \sin\phi \dfrac{T}{m} \\ \ddot{z} &= g-\cos\phi \cos\theta \dfrac{T}{m}\end{aligned}$$
이 방식대로 $\phi_{c}, \theta_{c}$를 계산하면 다음과 같다.
$$\dfrac{T}{m}=\dfrac{g-a_{z,c}}{\cos\phi\cos\theta}$$
이 식을 위의 식에 대입한다.
$$\begin{aligned} \phi_{c} &= \tan^{-1}\left( \dfrac{ a_{y,c} \cos\theta }{ g-a_{z,c}}\right) \\ \theta_{c} &= \tan^{-1} \left( \dfrac{ a_{x,c} }{ a_{z,c} - g } \right)$$
아마 실제로 코드를 구현하고자 한다면 역탄젠트의 부호문제 때문에 atan2를 쓸지 atan을 쓸지 고민을 해봐야할 것 같다.
3. 제어기
제어기 같은 경우에는 당연하게도 수많은 방법이 있다.
기본적으로는 PID / PD / PI / P 제어기를 필요에 맞게 골라 쓴다.
이 부분은 픽사호크 제어기를 분석할 때 더 자세히 다룰 것 같아서 PID를 보통 쓴다고만 알아둬도 문제 없을 듯하다.
다만 D 제어기는 미분값을 알아야하는데 예를 들어 각속도 제어기를 PID로 만드려면 각속도를 미분한 값을 써야한다. 그런데 각속도는 실제 센서 데이터값을 보면 굉장히 노이즈가 많이 들어가는 값이라서 수치미분으로 미분값을 구할 생각은 안하는 것이 좋은 것 같다.
[1] Beard, R. (2008). Quadrotor dynamics and control rev 0.1.
'항공우주 Aeronautical engineering' 카테고리의 다른 글
| [항공우주] Guidance, Navigation, and Control (GNC)란 무엇인가 (0) | 2023.12.07 |
|---|---|
| [비행동역학] Multicopter (Drone) dynamics (1) | 2023.11.08 |
| [비행동역학] Total angle of attack and Aerodynamic roll angle (0) | 2022.08.08 |
| [비행동역학] Coordinated turn과 원심력, 구심력에 대한 고찰 (0) | 2022.03.12 |
| [추진] 추진공학에 대한 개요 (2) 분류 (0) | 2022.03.02 |