보통 다루는 matrix가 square matrix라서 거의 생각을 안했는데 최근 제어 공부를 하다가
controllability matrix나 observability matrix가 rectangular matrix이어서
rectangular matrix에 대해서 좀 고민하게 되었습니다.
1. Rectangular matrix의 곱에서 singularity를 판별하는 문제

$A\in \mathbb{R}^{m\times n},B\in \mathbb{R}^{n\times m}\text{, where }m<n$가 있을 때
두 matrix의 곱의 차원을 살펴보겠습니다.
$AB\in \mathbb{R}^{m\times m}$
$BA\in \mathbb{R}^{n\times n}$
이 때 두 matrix의 곱은 둘 다 square matrix입니다. 이 matrix가 singular인지 nonsingular인지 알아보는 것이 이 글의 목적입니다.
위의 필기 그림 아래에 적은 것처럼 $BA$는 항상 singular하고, $AB$는 singular일 수도, nonsingular일 수도 있습니다. 물론 A가 $m<n$인 $m\times n$ matrix라는 것이 중요합니다.
$A$의 rank는 maximum이 m이고, $B$의 rank는 (명목 상) maximum이 n입니다. 하지만 $B$의 차원이 $n\times m$이므로, column이 m개가 한계이기 때문에 무조건 m 이하일 수밖에 없습니다.
그런데 $BA\in \mathbb{R}^{n\times n}$은 rank가 n이어야 nonsingular이지만, B가 가질 수 있는 independent vector는 m개가 최대이므로 아무리 weight를 가지고 조합을 해도 새로운 independent vector를 만들 수 없습니다. 즉, $BA$의 rank는 n이 될 수 없으므로 항상 singular입니다.
하지만 $AB\in \mathbb{R}^{m\times m}$은 rank가 m일 때 nonsingular인데, $A$와 $B$가 어떻게 되어있느냐에 따라 rank m일 가능성이 충분히 존재합니다.
위 필기에서도 나왔듯이
$rank(AB), rank(BA)\leq \min(rank(A),rank(B))\leq m <n$
이므로 nonsingular이기 위해 꼭 rank가 n이어야하는 $BA$의 경우는 아무리 해도 n이 될 수 없습니다.
아래는 예시입니다.

2. matrix와 그 Transpose of matrix의 product
그렇다면 어떤 rectangular matrix $A\in \mathbb{R}^{m\times n}$에 대해서 $A^{T}$와 Product하는 경우에 singularity는 어떨까요?
결론적으로 말하면,
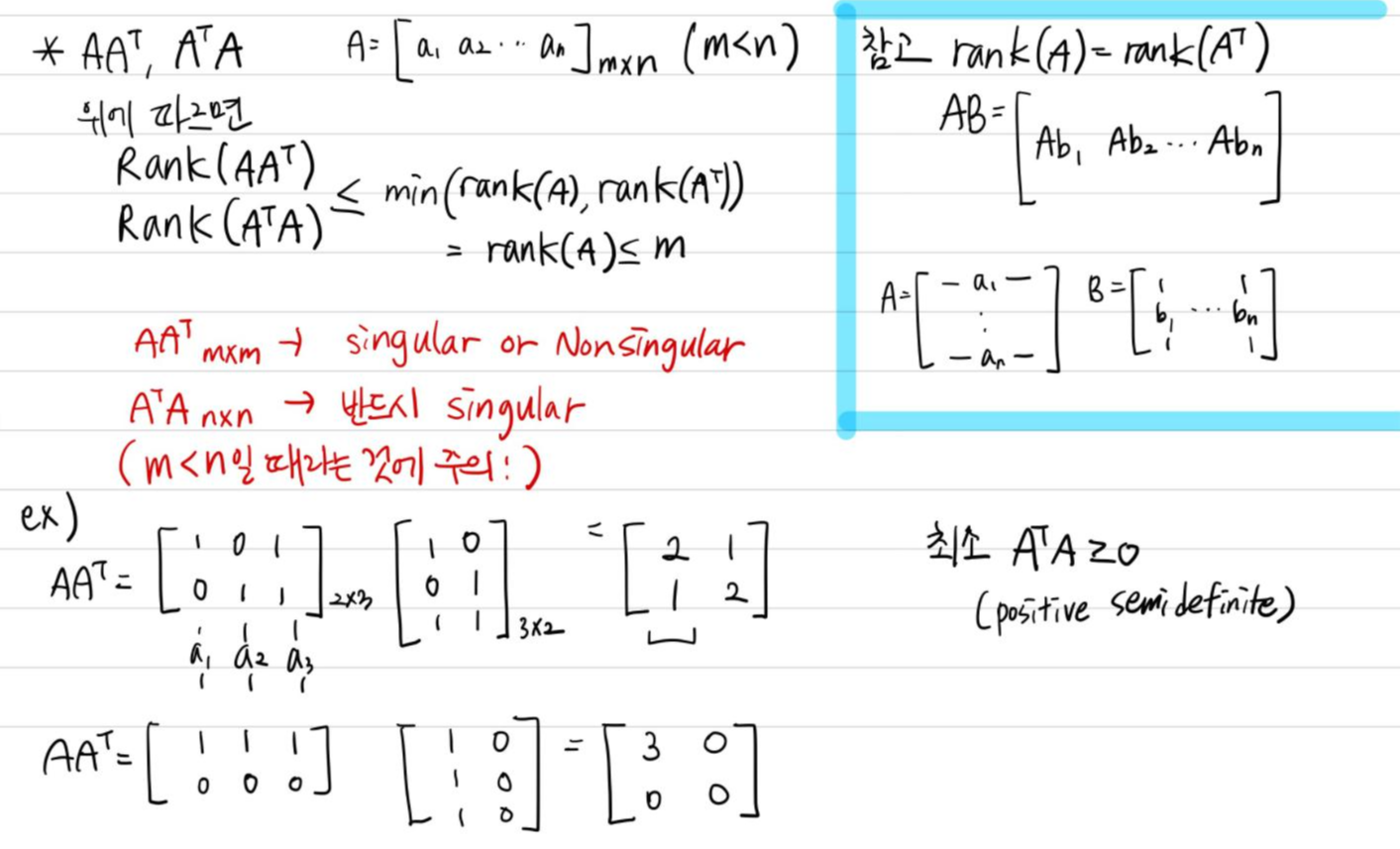
$A^{T}A\in \mathbb{R}^{n\times n}$은 rank m을 넘을 수 없으므로 항상 singular입니다.
그러나 $AA^{T} \in \mathbb{R}^{m\times m}$은 singular일 수도, nonsingular matrix일 수도 있음을 위에서 배운 것을 통해 알고 있습니다.
그런데 위에서 $AB$가 singular인지 nonsingular인지는 계산을 해봐야 알 수 있지만
$AA^{T}$의 경우에는 쉽게 알 수 있습니다. A가 rank m($\Rightarrow$ nonsingular)이면 $AA^{T}$는 rank n입니다.
$\text{Proof : }$
$rank(A)=m(\Rightarrow\text{ nonsingular})$일 때, $AA^{T}$가 nonsingular임을 증명하자.
$AA^{T}x=0$을 만족하는 $x$가 0 밖에 없음을 증명하면 됩니다.
$A\in \mathbb{R}^{m\times n}$가 rank m이면 non singular이므로 양변에 inverse를 곱할 수 있습니다.
$\Rightarrow A^{T}x=0$
그런데 $rank(A^{T})=rank(A)$이므로 $A^{T}$도 rank m입니다.
예를 들어 $A$가 $2\times 3$ matrix일 때, rank가 2라고 합시다. 그러면 $A^{T}$는 $3\times 2$ matrix일 때 rank가 2인 것입니다. 즉, independent column이 2개 입니다.
그렇다고 했을 때
$A^{T}x=0\Rightarrow x=0$
두 independent column을 조합해서 0을 만들 수 있는 weight vector $x$는 존재하지 않습니다. 0이어야만 합니다.
따라서 $AA^{T}$는 nonsingular입니다.
아래는 정리 및 예시이므로 참고해서 봐주세요.
'수학 Mathematics > 선형대수학 Linear Algebra' 카테고리의 다른 글
| [응용선형대수] Understanding Ax=0, Ax=b using null space matrix (0) | 2021.02.25 |
|---|---|
| [응용선형대수] Null space/Column space (0) | 2021.02.25 |
| [선형대수] QR decomposition (0) | 2021.02.20 |
| [응용선형대수] Vector Space/Subspace (0) | 2021.02.20 |
| [응용선형대수] LU Decomposition (0) | 2021.02.20 |