본인이 헷갈려서 정리하는 글
비행기에는 수많은 angle이 있는데 이게 오일러각과 맞물려서 애매하게 쓰이는 경우도 많아보인다.
조금씩 업데이트하면서 내용을 정리해갈 예정이다.
1. Bank angle
www.grc.nasa.gov/www/k-12/airplane/turns.html
Banking Turn
+ Text Only Site + Non-Flash Version + Contact Glenn
www.grc.nasa.gov


Bank angle은 roll angle $\phi$와 혼동이 있는 단어이다.
Euler angle에서 x축을 기준으로 정의된 roll angle은 비행체가 navigation frame에 대해서 특정 자세를 가지고 있을 때 3-2-1(yaw-pitch-roll)로 요각, 피치각, 롤각으로 좌표계 회전을 하면 동일하게 대응될 수 있으므로 모두의 합의 하에 요각, 피치각, 롤각을 정의한 것이다. 만약 3-2-1이 아니라 1-2-3 방식으로 정의하면 우리가 이미 알고있는 요각, 피치각, 롤각과 다른 값이 나올 것이다.
일반적인 오일러 각으로 정의된 롤각을 bank angle이라고 부를 수도 있지만, 다른 정의도 존재한다고 위 그림에 나와있다.
bank angle $\mu$는 y축과 수평면에 대한 각도로 정의할 수도 있다. 이는 롤각 $\phi$와 다르지만 요각과 피치각이 없을 때는 두 값이 동일할 것으로 예상할 수 있다.
2. slip-side angle 미끄럼각
비행기의 속도와 head의 방향의 차이가 달라서 생기는 각도
나는 북쪽으로 움직이고 있지만 heading을 바꿀 때 평형에 도달하기 전까지는 바람이 불어오는 방향(비행체 운동 방향)과 자세 방향 사이의 차이로 slip-side angle이 발생할 수 있다.

제가 어떤 사이트에서 왼쪽 그림을 보고 정리를 해보았습니다.

crab angle(=WCA=Wind correction angle) : course 방향과 heading 사이의 각도
course angle : north 방향을 기준으로 course 선의 각도
slip side angle : heading과 wind velocity 사이의 각도
3. Angle of attack

비행체의 reference line(airfoil의 chord line이라고 생각)과 상대적 바람 벡터 간의 각도를 angle of attack이라고 한다.
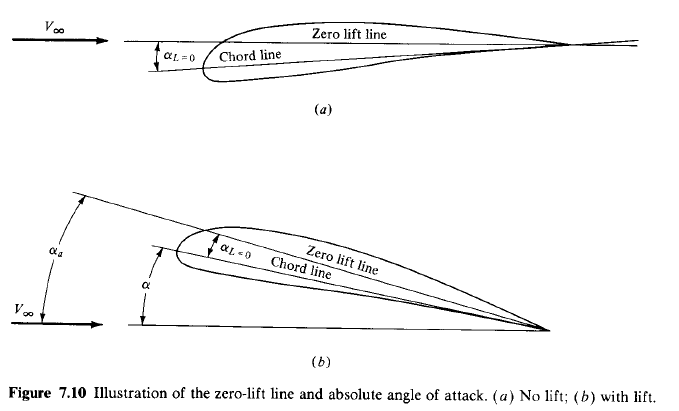
absolute angle of attack 이라는 개념이 따로 있다.
위의 그림(a)를 보면 받음각은 chord line을 기준으로 형성되지만, 특정 받음각에서 lift가 발생하지 않는다. 이 때의 각도를 기준으로 에어포일에 선을 그으면 zero lift line이라고 한다. 일반적인 에어포일은 zero lift line일 때의 받음각이 음수를 갖는다. (chord line을 기준으로 상대속도 벡터가 아래에 있을 때가 양수이다. 따라서 그림(a)은 받음각이 음수인 경우.)
absolute angle of attack은 실제 chord line을 기준으로 한 받음각이 아니라, zero lift line을 기준으로 한 받음각을 의미한다.
따라서 그림 (b)를 보면 absolute angle of attack은 다음과 같이 구해진다.
$\text{Absolute angle of attack : }\alpha_{a} = \alpha + \alpha_{L=0}$
4. Angle of Attack과 Side slip angle
받음각이나 옆미끄럼각은 비행체의 자세를 기준으로, 즉, 동체 좌표계를 기준으로 속도 벡터가 어떤 방향인지 나타날 때 사용한다.
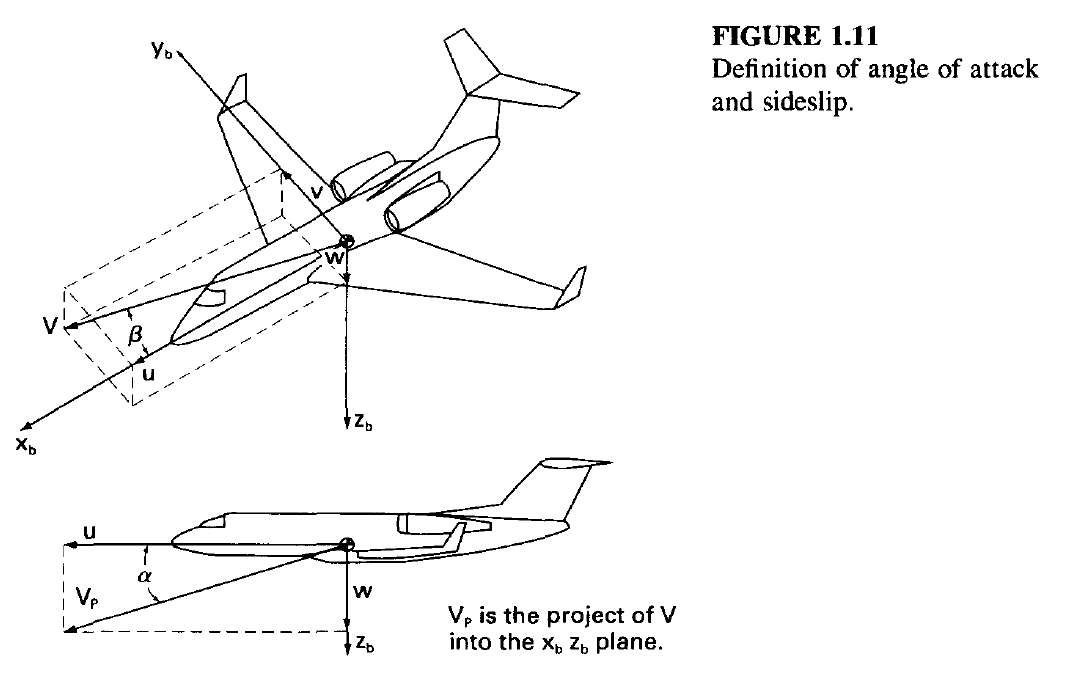
다음 그림을 보면 옆미끄럼각과 받음각에 대한 이해를 높일 수 있다.
받음각의 경우에는 xz평면에서 x축 방향 속도($u$)와 xz평면에 투영한 속도 벡터($V_{p}$) 사이의 각도로 정의된다.
속도 벡터가 $[u,v,w]^{\top}$일 때
$\alpha = \tan^{-1}\frac{w}{u}$
$\beta = \sin^{-1}\frac{v}{V}$
$\text{where } V=(u^{2}+v^{2}+w^{2})^{1/2}$
다음과 같이 정의된다. 이 식은 나중에 비행체 운동방정식에서 받음각이나 옆미끄럼각을 미분할 일이 있을 때 쓰인다.
참고문헌
Introduction to flight,
Flight stability and automatic control, Robert C. Nelson
'항공우주 Aeronautical engineering' 카테고리의 다른 글
| [항공우주] Airfoil 용어 정리 (0) | 2021.09.09 |
|---|---|
| 항공우주공학 영어단어 : 어원과 관련지어 정리 (0) | 2021.09.08 |
| [항공우주] 비행체 제어 - 좌표계 (0) | 2020.12.25 |
| [항공우주] 비행체 제어 - 오일러각 (0) | 2020.12.20 |
| [항공우주] 항공우주학개론 - 개요 (0) | 2020.10.08 |