서론
열심히 mpu-9250(9DOF IMU sensor)로 roll, pitch, yaw를 구하는 방법에 대해서 공부하다가 개념이 잘 이해가 가지 않아서 고민했습니다. 다들 저마다 설명을 하긴 하지만 무언가 명확하지는 않더군요.
예를 들면, 가속계에서 roll, pitch는 구할 수 있는데 왜 yaw는 구할 수 없는가? 물론 가속계만 두고 봤을 때 z축으로 회전을 하면 가속계 값 자체는 변하지 않으니까 당연하다고 볼 수 있습니다. 하지만 더 나아가서 생각해보면 z축 뿐 아니라 x축, y축으로도 조금씩 다 회전을 하면 어쨌든 roll, pitch, yaw가 뒤섞인 결과값이 나오니 방정식을 풀어서 yaw를 구할 수 없는 건가 궁금했습니다. 혹시 저와 같은 굴레에 빠지신 분이 있다면 이 글이 도움이 되길 바랍니다.
이 문제에 대한 해답은, 오일러각의 정의에 있었습니다.
# 오일러각의 정의
만약 지면좌표계(North East Down, NED)를 $\mathcal{F}^{i}$라고 하고, x축은 북쪽(north), y축은 동쪽(east), z축은 지구중심방향으로 하겠습니다. 지면좌표계는 비관성좌표계이기는 하나, 항공우주에서 주로 사용하는 좌표계입니다. 이 좌표계를 비행체 무게중심으로 옮기면 vehicle frame($\mathcal{F}^{v}$)라고 합니다. 똑같이 x축은 북쪽, y축은 동쪽, z축은 지구중심이지만 원점이 비행체에 고정된 것 뿐입니다. 북쪽, 동쪽, 지구중심은 항상 정해진 곳을 가리키지만 비행체는 움직이다보면 각 방향에 대해 기울어지기 마련입니다. 우리는 비행체의 자세를 명확하게 알 필요가 있기 때문에, 지면좌표계와 기체고정좌표계(body frame) 간의 관계를 알고 싶습니다.
body frame는 항공기 기체에 고정된 좌표계로, x축은 동체의 기수축, y축은 오른쪽 날개방향, z축은 오른손 법칙에 따라 동체 아래방향을 향하고 있습니다.
body frame을 $\mathcal{F}^{b}$라고 하겠습니다. 또한 이 body frame과 vehicle frame(또는 NED frame) 간의 자세각 차이를 각각 x,y,z축에 대한 회전각으로 롤각(roll, $\phi$), 피치각(pitch, $\theta$), 요각(yaw, $\psi$)으로 정의하겠습니다.
지면좌표계이자 vehicle frame($\mathcal{F}^{v}$)의 각 축을 $X_{1}Y_{1}Z_{1}$이라고 하고 처음에 $Z_{1}$축에 대하여 요각 $\psi$ 만큼 회전한 frame을 $\mathcal{F}^{2}$이라고 하겠습니다. 각 축은 $X_{2}Y_{2}Z_{2}$입니다.
또한 $Y_{2}$축에 대하여 피치각 $\theta$ 만큼 회전한 frame을 $\mathcal{F}^{3}$이라고 하고 각 축은 $X_{3}Y_{3}Z_{3}$입니다.
마지막으로 $X_{3}$축에 대하여 롤각 $\phi$ 만큼 회전한 frame은 우리가 최종적으로 구하고 싶었던 body frame $\mathcal{F}^{b}$이라고 하고 각 축은 $XYZ$입니다.
이러한 좌표계 변환을 3-2-1 변환이라고 하며, 이 때 정의된 요각, 피치각, 롤각을 오일러 각(eular angle)이라고 합니다.
**여기서 제가 착각했던 것은 왜 꼭 오일러각을 쓸 때 좌표계 변환을 요-피치-롤 순으로 회전하느냐는 것이었는데 애초에 정의가 그런 것이었습니다.
1단계) $\mathcal{F}^{v}\rightarrow \mathcal{F}^{2}$
이 경우 $Z_{1}$축에 대해 회전하는 것이므로 $X_{1}Y_{1}$평면에서 임의의 $\mathcal{F}^{v}$에서의 벡터 $\begin{pmatrix} U_{1}\\ V_{1}\\ W_{1} \end{pmatrix}$가 $\mathcal{F}^{2}$에서 어떻게 표현되는지 보겠습니다. 이 과정을 통해 rotation matrix를 구할 수 있습니다.
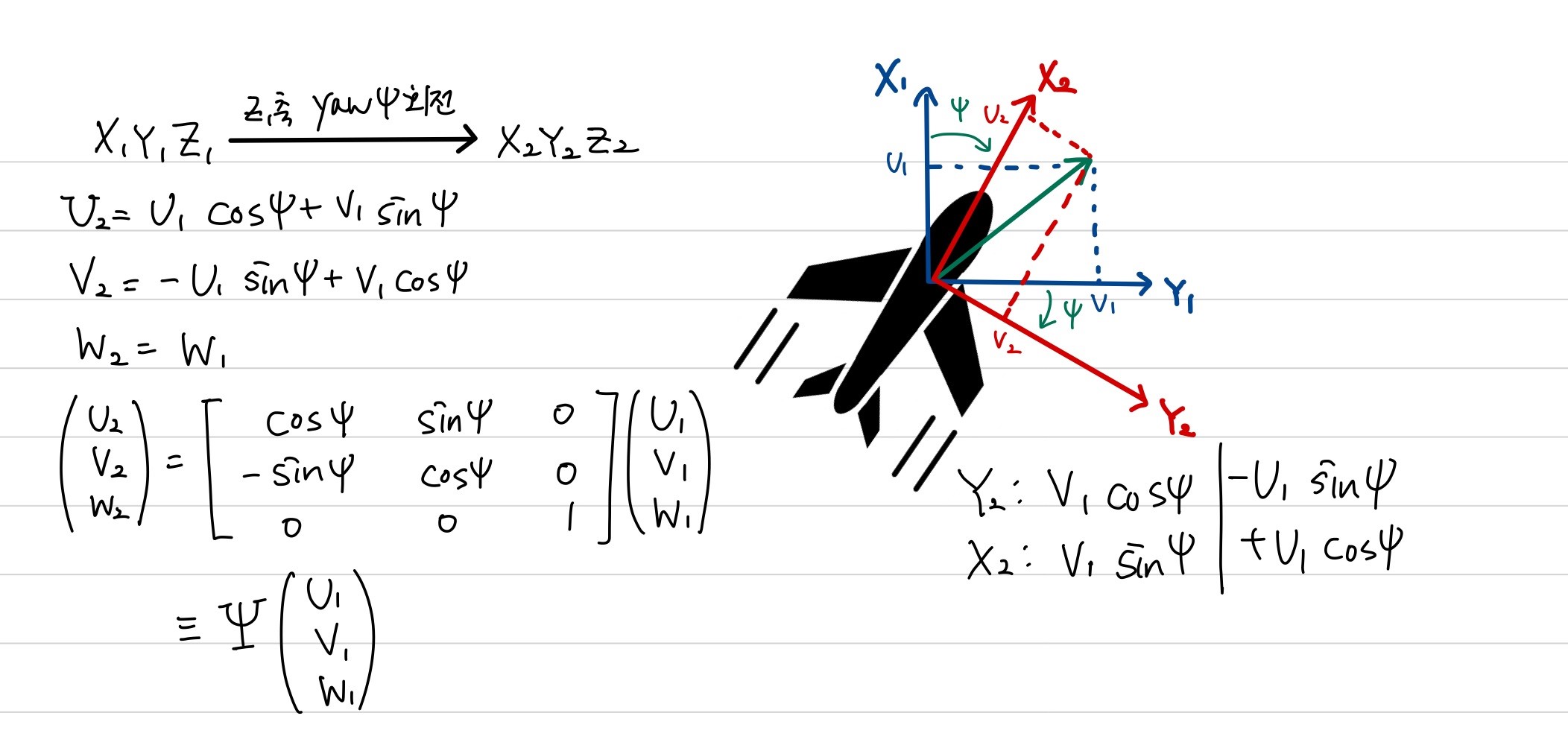
두 frame을 transform하는 $\text{rotation matrix }\Psi=\begin{bmatrix} \cos\psi & \sin\psi &0 \\ -\sin\psi & \cos\psi &0 \\ 0 & 0 & 1 \end{bmatrix}$
이 변환을 계산할 때 주의할 점은 z축 방향이 지면 쪽을 향하고 있기 때문에 오른손을 이용해서 +방향 요각으로 설정하고 구해야한다는 것입니다. 위 그림에서 시계방향이 아닌, 시계반대방향으로 요각이 형성되었다면 rotation matrix이 지금과는 다르기 때문입니다.
2단계) $\mathcal{F}^{2} \rightarrow \mathcal{F}^{3}$
이 경우 $Y_{2}$축에 대해 회전하는 것이므로 $X_{2}Z_{2}$평면에서 임의의 $\mathcal{F}^{2}$에서의 벡터 $\begin{pmatrix} U_{2}\\ V_{2}\\ W_{2} \end{pmatrix}$가 $\mathcal{F}^{3}$에서 어떻게 표현되는지 보겠습니다. 이 과정을 통해 rotation matrix를 구할 수 있습니다.

$\text{Rotation matrix }\Theta=\begin{bmatrix} \cos\theta & 0 & -\sin\theta\\ 0 & 1 & 0 \\ \sin\theta & 0 & \cos\theta \end{bmatrix}$
3단계) $\mathcal{F}^{3} \rightarrow \mathcal{F}^{b}$
계속 해온 것처럼 $X_{3}$축에 대해 회전하는 것이므로 $Y_{3}Z_{3}$평면에서 임의의 $\mathcal{F}^{3}$에서의 벡터 $\begin{pmatrix} U_{3}\\ V_{3}\\ W_{3} \end{pmatrix}$가 $\mathcal{F}^{b}$에서 어떻게 표현되는지 보겠습니다.

$\text{Rotation matrix }\Phi=\begin{bmatrix}1 & 0 &0 \\ 0 & \cos\phi& \sin\phi \\ 0 & -\sin\phi & \cos\phi\end{bmatrix}$
4단계) $\mathcal{F}^{v} \rightarrow \mathcal{F}^{b}$
결국 우리의 목표는 vehicle frame(이자 지면좌표계)에서 body frame으로 바꾸는 것이 목표였기 때문에
$\mathcal{F}^{v}$의 임의의 벡터 $\begin{pmatrix} U_{1}\\ V_{1}\\ W_{1} \end{pmatrix}$를 $\mathcal{F}^{b}$의 임의의 벡터 $\begin{pmatrix} U\\ V\\ W \end{pmatrix}$로 바꾸는 것이다.
따라서
$\begin{pmatrix} U\\ V\\ W \end{pmatrix}=\Phi\Theta\Psi\begin{pmatrix} U_{1}\\ V_{1}\\ W_{1} \end{pmatrix}$
$\Phi\Theta\Psi$를 계산하면
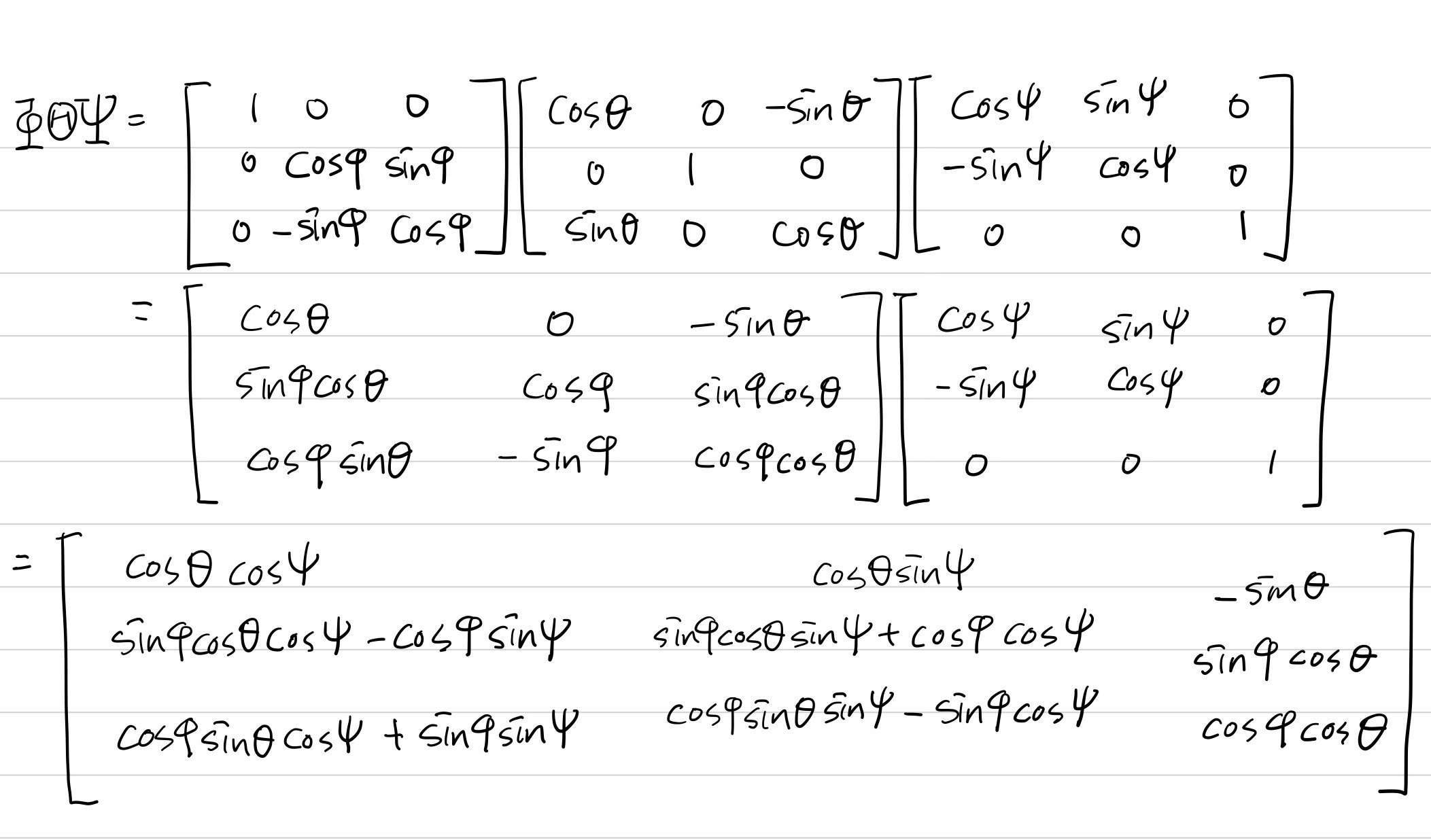
다음과 같이 나옵니다. 이 matrix가 지면좌표계이자 vehicle frame에서 body frame으로 바꿔주는 좌표변환행렬입니다.
Q. 왜 가속도계(Accelerometer)는 요각(yaw)을 구할 수 없을까?
이제 처음에 제가 했던 의문으로 돌아가보면, imu 센서가 왜 roll, pitch는 구할 수 있는데 yaw는 구할 수 없느냐는 문제였습니다. 이 문제는 위의 좌표변환행렬을 통해 이해할 수 있습니다.

만약 가속도계가 얌전히 지면에 놓여있다고 생각하면 이 가속도계가 느끼는 것은 중력 뿐입니다. 따라서 결과값은 z축으로 $+9.8m/s^{2}$을 가집니다. (x축, y축은 0)
만약 이 가속도계를 이리저리 회전해두면 특별히 외부힘이 없다고 생각할 때 오직 중력을 측정하지만, 이 때는 z축 값 뿐 아니라 x축, y축 성분도 가지게 됩니다. 위에서 기울어진 가속도계를 보면 쉽게 이해가 가실 겁니다. 그럼 이렇게 가속도계가 기울어진 상황에서 x축, y축, z축 성분은 각각 어떤 의미일까요?
이 상황은 위에서 계속 이야기한, 지면자표계에서 body frame으로 중력가속도에 해당하는 벡터를 변환하는 것과 동일한 상황입니다.
지면좌표계에서 중력가속도 벡터는 $\begin{pmatrix} 0\\ 0\\ +g \end{pmatrix}$입니다. 각 축마다 롤각, 피치각, 요각으로 회전했다고 보면 좌표변환행렬을 곱함으로써, 새로운 가속도계에 대한 중력 가속도 벡터의 x,y,z 방향 성분을 구할 수 있습니다.

이 벡터를 좌표변환행렬과 곱하면 아래의 matrix처럼 $\begin{bmatrix} -g\sin\theta\\ g\cos\theta\sin\phi\\ g\cos\theta\cos\phi \end{bmatrix}$가 나타납니다.
여기서 주목할 사실은 중력가속도 벡터를 변환해도 요각($\psi$)은 matrix에 포함되어 있지 않는다는 것입니다.
그 말은 곧 가속도계로 x,y,z값을 측정하더라도 matrix에는 요각이 없으므로 방정식을 풀어도 요각을 구할 방법은 없습니다.
그래서 위에서 구한 좌표변환행렬을 $\Phi\Theta\Psi$가 아닌 $\Psi\Theta\Phi$, 이런식으로 바꾸면 가속도계로 요각을 구할 수 있지 않을까 생각했습니다.
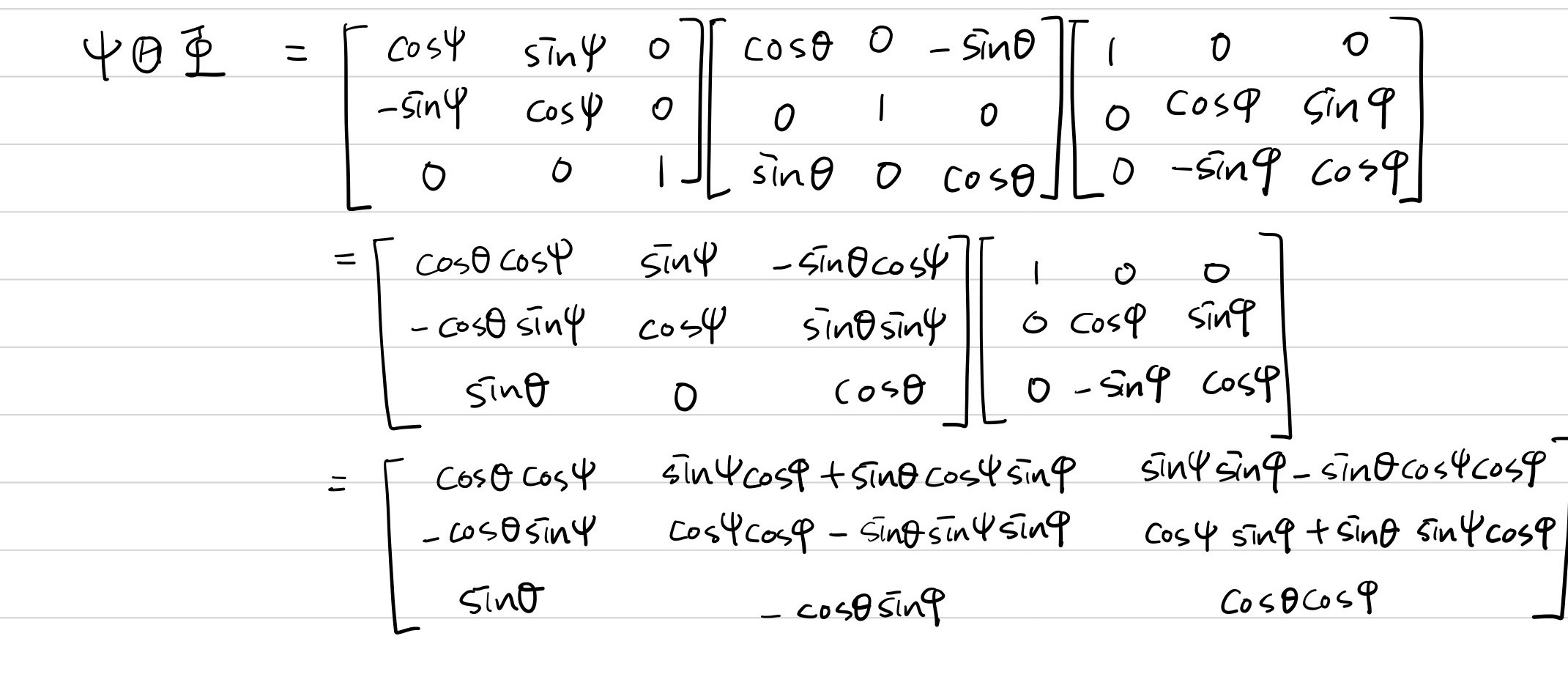
이렇게 좌표변환행렬을 정의한다면 중력가속도 벡터 $\begin{pmatrix} 0\\ 0\\ +g \end{pmatrix}$를 곱하더라도 롤각, 피치각, 요각 성분이 모두 남아있으므로 3개의 연립방정식을 풀어서 모든 각을 구할 수 있습니다.
(직접 위의 matrix와 중력가속도 벡터를 곱해보시면 쉽게 이해가 됩니다.)
하지만 위에서 제가 언급했듯이 롤, 피치, 요라는 오일러 각의 정의 상 $\Psi\Theta\Phi$와 같은 방식으로 좌표변환행렬을 곱하는 것은 정의에 어긋나는 것이므로 불가능합니다. (여기서는 오일러 각의 정의가 3-2-1이기 때문에 불가능한 것이고 다른 오일러각 정의로 해결할 수 있다는 점을 강조하고 싶습니다.)
따라서 우리는 가속도계만으로는 요각을 구할 수 없다는 한계를 수식적으로도 이해할 수 있습니다.
참고자료
김병수 외 4명, 비행동역학 및 제어, 경문사, 2004
FARI, STEFANO. "Guidance and control for a fixed-wing UAV." (2017).
추후에 좌표계에 대한 포스팅도 진행하면 좋을 듯합니다.
'항공우주 Aeronautical engineering' 카테고리의 다른 글
| [항공우주] Airfoil 용어 정리 (0) | 2021.09.09 |
|---|---|
| 항공우주공학 영어단어 : 어원과 관련지어 정리 (0) | 2021.09.08 |
| [항공우주] bank angle, slip-side angle, angle of attack (0) | 2021.03.02 |
| [항공우주] 비행체 제어 - 좌표계 (0) | 2020.12.25 |
| [항공우주] 항공우주학개론 - 개요 (0) | 2020.10.08 |