비행체 제어에서 쓰이는 좌표계에 대해 정리를 하려고 합니다.
비행체 제어는 쓰임에 따라 좌표계를 바꿔쓰는 것으로 보입니다. 각각의 좌표계에 대한 이해가 있어야, 쓰임에 맞게 좌표계를 정하고 식을 유도할 수 있을 것입니다.
*Latitude : 위도
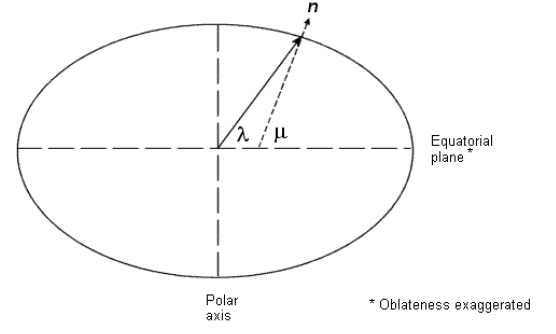
*Geocentric latitude($\lambda$) : 지구중심 위도, 지구 중심에서 지구 표면까지 radius vector를 표시했을 때 적도면과 이루는 각
*Geodetic latitude($\mu$) : 지표 위도, 지구 표면에서 수직한 벡터를 표시할 때 이 벡터가 적도면과 이루는 각
$\rightarrow$ 지구가 완벽한 구형이라면 geocentric latitude와 geodetic latitude는 일치하지만, 지구는 완벽한 구형이 아닌 타원형이므로 약간의 차이가 발생합니다.
*Longitude : 경도
1. 관성좌표계 vs 비관성좌표계
제가 고등학교 물리를 배울 때, 맨 처음에 뉴턴의 3법칙을 배웁니다. 그 때 뉴턴 법칙을 알면서 물체의 질량과 힘, 가속도 간의 관계를 알고 이를 통해 물체의 움직임을 해석할 수 있게 되는데요, 이에 대한 법칙이 깨지는 것이(엄밀히 말하면 뉴턴 법칙이 적용되는 상황이 아닐 때) 아인슈타인의 상대성이론을 배우는 부분부터입니다.
제가 아인슈타인의 상대성 이론에 대해 기초적인 지식 밖에는 없어서 자세히 말할 수는 없지만, 서로 다른 관성계에 같은 현상이 다르게 관측될 수 있음은 다들 알고 계실 겁니다.
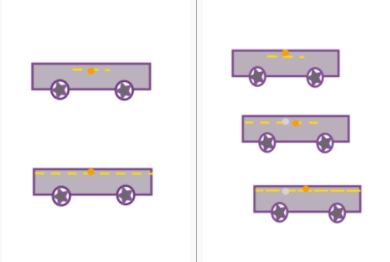
출처 : ko.wikipedia.org/wiki/%ED%8A%B9%EC%88%98_%EC%83%81%EB%8C%80%EC%84%B1%EC%9D%B4%EB%A1%A0
위의 그림처럼 좌표계에 따라 버스 앞뒤에 동시에 빛이 닿는 사건이 다른 좌표계에서는 뒤에 먼저 빛이 닿는 현상처럼 보입니다.
다만 등속운동을 한다해도 위의 사례와 같은 동시성의 상대성은 일어날 수 있습니다만, 뉴턴의 법칙은 적용될 수 있습니다.
하지만 가속계에서는 뉴턴의 법칙이 성립할 수 없고, 이를 만족시키기 위해 관성력(예를 들면 원심력)같은 개념을 도입하여 뉴턴의 법칙이 성립하도록 만듭니다.
우리는 뉴턴 역학을 기준으로 생각하기 때문에 이 뉴턴 법칙이 적용될 수 있는 좌표계를 정의합니다.
관성좌표계는 우주에 고정되어 있는 좌표계로, 뉴턴의 제 2법칙을 적용할 수 있는 유일한 좌표계입니다.(비행동역학 및 제어)
정지해있거나 등속 운동을 하는 좌표계를 관성 좌표계로 볼 수 있습니다. 이 좌표계에서는 뉴턴 법칙이 성립하기 때문입니다.
그 외에 가속하거나 회전하는 좌표계는 비관성 좌표계로 볼 수 있을 것입니다.
2. 지구중심 관성 좌표계(Earth Centered Inertial, ECI)
지구중심을 원점에 두고 지구와 함께 병진운동을 하고 있으나 회전하고 있지 않은 좌표계를 관성좌표계 말합니다.
항공기와 같이 지구에서 운항하는 비행체에 적용할 수 있는 좌표계입니다. 지구가 등속운동하고 있지 않다면 지구와 함께 병진운동하는 게 관성좌표계로 볼 수 있을까, 하는 의문이 들 수 있습니다. 하지만 지구 상의 운동으로 봤을 때 관성좌표계로 봐도 무방합니다.
X축 : vernal quinox(춘분점)를 가리키는 방향
Y축 : equatorial(적도) 평면에서 X축에서 동쪽으로 90도 기울어진 방향
Z축 : 지구자전축의 북쪽 방향
3. 지구중심 지구고정 좌표계(Earth Centered Earth Fixed, ECEF)
ECI와 같이 지구중심에 원점을 두고 있지만, 차이점이 있다면 지구와 함께 자전운동도 합니다. 즉, 지구중심을 두고 지구에 고정된 좌표계
자전운동을 하고 있다는 점에서 비관성 좌표계임을 알 수 있습니다.
X축 : 적도 평면과 prime meridian(본초 자오선)의 교차점으로 뻗어가는 방향
Y축 : X축과 Z축에 수직한 방향이면서 동쪽 사분면을 향하는 방향(RH rule(Right Hand rule, 오른손 법칙)을 지키도록)
Z축 : 지구자전축의 북쪽 방향

4. 지면 좌표계(North East Down, NED)
지면좌표계는 비관성좌표계로, 원점은 지표면에 있으며 지구와 함께 자전운동을 하는 좌표계입니다. 즉 지구중심 지구고정 좌표계처럼 지구에 고정되어 있는 좌표계입니다.
X축 : 북쪽(북극을 향하는 방향)
Y축 : 동쪽(위도선과 평행한 방향)
Z축 : 지구표면에 수직하게 지구중심으로 들어가는 방향

5. 기체고정 좌표계(Body-Fixed)
1) 기체고정 좌표계
기체고정 좌표계는 말 그대로 비행체에 고정된 좌표계입니다.
X축은 동체의 기수축, Y축은 오른쪽 날개 방향, Z축은 동체 아랫방향
지면좌표계와 기체고정좌표계는 오일러 각(euler angle, $\phi,\theta,\psi$)만큼 차이가 납니다.
기체고정좌표계에 대해서 관성모멘트(Moment of Inertia)가 일정하므로 모멘트 방정식을 기술할 때 편리합니다.
2) 안정성 좌표계(stability frame)

주변 공기에 대해 상대적인 비행체 속도를 Airspeed, $V_{a}$라고 하겠습니다. 이 때 적절한 양력을 받기 위해서는 이 airspeed가 날개와 양의 각도를 이루고 있어야 합니다. 위의 그림에서 $\alpha$가 날개와 airspeed 사이의 각도이고 그림과 같을 때 양(+)입니다. 이것을 받음각(AOA, Angle of Attack)이라고 합니다.
안정성 좌표계($\mathcal{F}^{s}$)는 기체고정 좌표계($\mathcal{F}^{b}$)에서 Y축에 대하여 받음각($\alpha$)만큼 회전한 좌표계를 말합니다.
$\mathcal{F}^{b}\rightarrow \mathcal{F}^{s}$
기체고정 좌표계에서 안정성 좌표계로 변환하는 matrix는
$\text{Rotation matrix }\mathcal{R}_{b}^{s}(\alpha)=\begin{bmatrix} \cos\alpha & 0 & -\sin\alpha \\ 0 & 1 & 0 \\ \sin\alpha & 0 & \cos\alpha \end{bmatrix}$
3) 바람 좌표계 (wind frame)

비행체의 airspeed 벡터가 항공기 좌우대칭 평면 상에 있지 않는 경우 옆미끄럼각(slipside angle, $\beta$)이 존재합니다. 안정성 좌표계가 받음각$\alpha$만큼 좌표계를 회전한 것이라면, 이 안정성 좌표계에서 Z축에 대하여 옆미끄럼각만큼 회전하면 바람이 불어오는 방향과 일치하는 좌표계를 구할 수 있습니다. 이것을 바람 좌표계라고 합니다.
$\mathcal{F}^{s}\rightarrow \mathcal{F}^{w}$
안정성 좌표계에서 바람 좌표계로 변환하는 matrix는 다음과 같습니다.
$\text{Rotation matrix }\mathcal{R}_{s}^{w}(\beta)=\begin{bmatrix} \cos\beta & -\sin\beta & 0 \\ \sin\beta & \cos\beta & 0 \\ 0 & 0 & 1 \end{bmatrix}$
따라서 기체고정 좌표계에서 바람 좌표계로 변환하는 matrix는
$\mathcal{R}_{s}^{w}(\beta)\mathcal{R}_{b}^{s}(\alpha)=\begin{bmatrix}\cos\beta\cos\alpha & \sin\beta & \cos\beta\sin\alpha \\ -\sin\beta\cos\alpha & \cos\beta & -\sin\beta\sin\alpha\\ -\sin\alpha & 0 &\cos\alpha \end{bmatrix}$
참고자료
MATLAB Aerospace Toolbox User's Guide
김병수 외 4명, 비행동역학 및 제어, 경문사, 2004
FARI, STEFANO. "Guidance and control for a fixed-wing UAV." (2017).
용어정리 (출처: 표준국어대사전)
춘분점(vernal equinox) : 태양이 황도를 따라 남쪽에서 북쪽으로 지나가면서 하늘의 적도와 만나는 점
황도(the cliptic) : 태양의 둘레를 도는 지구의 궤도가 천구에 투영된 궤도. 천구의 적도면에 대하여 황도는 약 23도 27분 기울어져 있으며, 적도와 만나는 두 점을 각각 춘분점, 추분점이라고 한다.
황도면(the plane of the ecliptic) : 지구의 공전 궤도면을 천구 위에 투영한 평면
천구(celestial sphere) : 천체의 시위치를 정하기 위하여 관측자를 중심으로 하는 무한 반경의 큰 구면. 모든 천체가 실제 거리와는 관계없이 이 구면 위에 투영되어 있는 것으로 본다.
equinox 주야 평분시(춘분 또는 추분) - vernal equinox(춘분점), autumnal equinox(추분점)
solstice 지점(하지 또는 동지) - summer solstice(하지), winter solstice(동지)

'항공우주 Aeronautical engineering' 카테고리의 다른 글
| [항공우주] Airfoil 용어 정리 (0) | 2021.09.09 |
|---|---|
| 항공우주공학 영어단어 : 어원과 관련지어 정리 (0) | 2021.09.08 |
| [항공우주] bank angle, slip-side angle, angle of attack (0) | 2021.03.02 |
| [항공우주] 비행체 제어 - 오일러각 (0) | 2020.12.20 |
| [항공우주] 항공우주학개론 - 개요 (0) | 2020.10.08 |