1. Length of vectors
$\begin{bmatrix}x_{1}\\ \vdots\\ x_{n}\end{bmatrix}\in\mathbb{R}^{n}$
vector의 길이($\left \| x \right \|$)에 대한 식은 다음과 같습니다
$\left \| x \right \|=\sqrt{x_{1}^{2}+x_{2}^{2}+\cdots+x_{n}^{2}}=x^{T}x$
2. Orthogonality
$x,y\in \mathbb{R}^{n}$
x,y라는 n차원 벡터가 있을 때 두 벡터가 수직이라고 해보자.

피타고라스 공식에 의해
$\left \| x-y \right \|^{2}=\left \| x \right \|^{2}+\left \| y \right \|^{2}\cdots (1)$이 성립합니다.
또한 $\left \| x-y \right \|^{2}$은 $(x^{T}-y^{T})(x-y)$와 같습니다. 따라서
$(x^{T}-y^{T})(x-y)=x^{T}x+y^{T}y-x^{T}y-y^{T}x=\left \| x \right \|^{2}+\left \| y \right \|^{2}-2x^{T}y\cdots (2)$
위에서 구한 두 식은 같으므로 $\left \| x \right \|^{2}+\left \| y \right \|^{2}=(1)=(2)=\left \| x \right \|^{2}+\left \| y \right \|^{2}-2x^{T}y$
$\therefore x^{T}y=0$
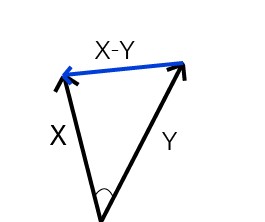
만약 두 벡터가 이루는 각이 $\frac{\pi}{2}$보다 작다면
$\left \| x-y \right \|^{2}=\left \| x \right \|^{2}+\left \| y \right \|^{2}-2x^{T}y< \left \| x \right \|^{2}+\left \| y \right \|^{2}$

만약 두 벡터가 이루는 각이 $\frac{\pi}{2}$보다 크다면
$\left \| x-y \right \|^{2}=\left \| x \right \|^{2}+\left \| y \right \|^{2}-2x^{T}y > \left \| x \right \|^{2}+\left \| y \right \|^{2}$
이 과정을 정리해보도록 하겠습니다.
$\text{Definition) }$
$\text{(1). }(x,y)=x^{T}y=x_{1}y_{1}+x_{2}y_{2}+\cdots+x_{n}y_{n}$
$\text{(2). x and y are orthogonal if and only if }x^{T}y=0$
위의 설명에서 두 벡터 사이의 각도를 $\theta$라고 할 때,
$\theta <\frac{\pi}{2}$이면 $x^{T}y>0\Rightarrow \left \| x \right \|^{2}+\left \| y \right \|^{2}-2x^{T}y< \left \| x \right \|^{2}+\left \| y \right \|^{2}$
$\theta > \frac{\pi}{2}$이면 $x^{T}y<0\Rightarrow \left \| x \right \|^{2}+\left \| y \right \|^{2}-2x^{T}y > \left \| x \right \|^{2}+\left \| y \right \|^{2}$
이는 고등학생 때 배웠던 내적공식 $x\cdot y =|x||y|\cos\theta$와도 일치하는 내용입니다.
$\text{Remark) }$
$\text{(1). 0 is orthogonal to any vector in }\mathbb{R}^{n}$
$\text{(2). If x is orthogonal to x, then x=0}\Leftrightarrow \left \| x \right \|^{2}=x^{T}x=0$
$\text{Theorem) }$
$\text{The non-zero vectors }v_{1},v_{2},\ldots,v_{n} \text{ are mutually orthogonal }(v_{i})\bot (v_{j})\text{ for }i\neq j$
$\text{Then }v_{1},v_{2},\ldots,v_{n}\text{ are linearly independent.}$
$\text{Proof) }$
$\text{We need to show that if }c_{1}v_{1}+c_{2}v_{2}+\cdots+c_{n}v_{n}=0 \text{ then }c_{1}=c_{2}=\ldots=c_{n}=0$
$\text{consider }v_{1}^{T}(c_{1}v_{1}+c_{2}v_{2}+\cdots+c_{n}v_{n})=0$
$c_{1}v_{1}^{T}v_{1}+c_{2}v_{1}^{T}v_{2}+\cdots+c_{n}v_{1}^{T}v_{n}=0$
모든 벡터가 서로 orthogonal이므로 $v_{i}^{T}v_{j}=0$
$c_{1}||v_{1}||^{2}=0 \Rightarrow c_{1}=0$
마찬가지로 $v_{i}^{T}(c_{1}v_{1}+\ldots+c_{n}v_{n})=0$이면 $c_{i}=0$
즉, 모든 c항이 0이므로 linearly independent임이 증명되었습니다.
3. Orthogonal basis
$\text{Definition) }$
$\text{V = a vector space}$
$\text{(1). a basis }v_{1},v_{2},\ldots,v_{n} \text{ of V is called an orthogonal basis if }v_{i}\bot v_{j}\forall i\neq j$
$\text{(2). a basis }v_{1},v_{2},\ldots,v_{n} \text{ of V is called an orthonormal basis if }v_{i}\bot v_{j}\forall i\neq j$
$\left \|v_{i}\right \|=1 \forall i$
길이에 상관없이 각 벡터가 수직이면 linearly independent하므로 basis입니다. 여기서 길이 1이면 orthonormal basis입니다.
$v_{1},v_{2},\ldots,v_{n} \text{ form an orthogonal basis of V }$
$\text{if }v=c_{1}v_{1}+c_{2}v_{2}+\cdots+c_{n}v_{n}\text{ then }c_{i}=v_{i}^{T}v$
$\text{Proof) }v_{1}^{T}v=v_{1}^{T}(c_{1}v_{1}+\cdots+c_{n}v_{n})=c_{1}$
NOTE : $v_{1},v_{2},\cdots,v_{n}$ 가 an orthogonal basis of $V$를 이룰 때
$v=c_{1}v_{1}+\cdots+c_{n}v_{n}$이면 $c_{i}=v_{i}^{\top}v$.
4. Orthogonal spaces

$\text{ex) }$
$V : x+y+z=0 \text{ in }\mathbb{R}^{3}$
$W=\left\{a\begin{bmatrix}1\\1\\1\end{bmatrix},a\in\mathbb{R}\right\}$
그림 상으로 보았을 때 두 vector space는 orthogonal합니다.
$\text{Definition) }$
$\text{V, W : two subspaces}$
$\text{V and W are orthogonal if }V\perp W \text{ for any }v\in V \text{ and }w\in W$
$\text{ex) suppose that }\left\{\begin{matrix}
v_{1},\ldots,v_{n}\text{ span V}\\
w_{1},\ldots,w_{n}\text{ span W}
\end{matrix}\right.$
$\text{Then, }V\perp W \Leftrightarrow v_{i}\perp w_{j}\text{ for any }i,j$
예를 들어 $\text{In } \mathbb{R}^{4}$
$V \text{ is spanned by }\begin{bmatrix}1\\ 0\\ 0\\ 0\end{bmatrix}\text{ and }\begin{bmatrix}1\\ 1\\ 0\\ 0\end{bmatrix}$
$W \text{ is spanned by }\begin{bmatrix}0\\ 0\\ 1\\ 1\end{bmatrix}$
보시면 $\begin{bmatrix}1\\ 0\\ 0\\ 0\end{bmatrix}\perp \begin{bmatrix}0\\ 0\\ 1\\ 1\end{bmatrix}$이고
$\begin{bmatrix}1\\ 0\\ 0\\ 0\end{bmatrix}\perp \begin{bmatrix}0\\ 0\\ 1\\ 1\end{bmatrix}$이므로
각 vector space에 속한 벡터들이 서로 orthogonal하므로 $V\perp W$입니다.
만약 $L$이라는 Vector space가 $\begin{bmatrix}0\\ 0\\ -1\\ 1\end{bmatrix}$으로 span되는 vector space라면
이 벡터는 위의 $V,W$를 span하는 벡터들과 모두 orthogonal하므로
$L\perp V \text{ and }L\perp W$ 임을 알 수 있습니다.
여기서 질문 : $\text{What space can be orthogonal to L,V,W?}$
정답은 ${0}$ 영벡터입니다.
지금 보시면 L은 rank 1이고(basis element가 1개), V는 rank 2, W는 rank 1입니다.
$\mathbb{R}^{4}$에서 orthogonal한 vector space의 rank 총합이 4이므로, 이미 다른 linearly independent vector를 찾을 수 없습니다. 따라서 영벡터 외에는 $L,V,W$와 수직인 Vector space를 찾을 수 없습니다.
$\textbf{Fundamental theorem of orthogonality}$
그 전 글에서 배웠던 4개의 fundamental space를 다시 언급하려고 합니다.
Column space, Row space, Null space, Left null space를 orthogonal 관계로 설명할 수 있습니다.
$\text{Theorem) A : }m\times n\text{ matrix}$
$N(A)\perp C(A^{T})\text{ and }N(A^{T})\perp C(A)$
$\text{proof) }$
① $N(A)\perp C(A^{T})$ 첫 번째 증명 방법
$x\in N(A)$
$\begin{bmatrix} \text{row 1} \\ \text{row 2} \\ \vdots \\ \text{row n} \end{bmatrix}\begin{bmatrix} \\ x \\ \\ \end{bmatrix}=\begin{bmatrix} \\ 0 \\ \\ \end{bmatrix}$
즉, $\text{row i}\begin{bmatrix} \\ x \\ \\ \end{bmatrix}=0\Leftrightarrow \text{row i}\perp x \forall i$
따라서 row space의 basis와 null space를 span하는 basis vector가 orthogonal이므로 두 space 역시 orthogonal입니다.
$\text{row i}\perp x \Rightarrow N(A)\perp C(A^{T})$
② 두 번째 증명 방법
$\text{For }x\in N(A) \text{ and }y\in C(A^{T}) (y=A^{T}u \text{ for some u})$
증명을 위해서는 $y^{T}x=0 \Leftrightarrow x\perp y$임을 보여야합니다.
$y^{T}x=(A^{T}u)^{T}x=(u^{T}A)x=u^{T}(Ax)=0 (\because Ax=0)$
$N(A^{T})\perp C(A)$도 비슷한 방법들로 증명할 수 있습니다.
정리하면
$A:\mathbb{R}^{n}\rightarrow \mathbb{R}^{m} \rightarrow A \in \mathbb{R}^{m\times n}$
$\dim C(A)=\dim C(A^{T}) = \text{rank }n$ (matrix와 그 matrix의 transpose는 차원이 동일합니다.)
$\dim N(A)+\dim C(A^{T}) = n$
$\dim N(A^{T})+\dim C(A) =m$
matrix는 n차원에서 m차원으로 mapping하는 linear transformation으로 볼 수 있습니다.
$C(A)$는 A의 column으로 mapping한 것이므로 m차원 안에 속해있으며 column이 basis이냐, 아니냐에 따라 m차원을 모두 span할 수 있는지 아닌지가 결정됩니다. 같은 m차원 안에서 left nullspace는 $C(A)$와 수직인 관계를 가집니다.
유시하게 Row space($C(A^{T})$)는 n차원 안에 속하면서 row로 만들 수 있는 vector space가 됩니다. 같은 n차원에 속하면서 row space와 orthogonal한 nullspace도 있습니다.
이 관계를 잘 나타낸 것이 바로 아래 그림입니다.

5. Orthocomplement
$\text{Definition)}$
$\text{V : a subspace}$
$\text{orthocomplement of V which is denoted by }V^{\perp}$
$\text{is given by }V^{\perp}=\{w : w \perp v \text{ for any }v \in V \}$
- orthocomplement의 성질
$\text{(1). }V^{\perp} \text{ is a subspace}$
$\text{(2). }\dim V^{\perp}+\dim V =\text{ dim of total space}$
$\text{(3). If }V\subseteq \mathbb{R}^{n} \text{ a subspace}$
$\mathbb{R}^{n}=V \oplus V^{\perp}$
$\text{meaning for any }x\in \mathbb{R}^{n}\text{, there are unique }x_{1}\in V_{1}, x_{2}\in V^{\perp}\text{ such that }x=x_{1}+x_{2}$
$\text{(4). }(V^{\perp})^{\perp}=V$
이제 vector space와 그 vector space의 orthocomplement과의 관계를 알아보겠습니다.
$V\subseteq \mathbb{R}^{n} \text{ a subspace}$
$\text{orthocomplement }V^{\perp}=\{w:w\perp v \forall v \in V \}$
$\text{(1). }V^{\perp} \text{ is a vector space}$
$v+w\in V^{\perp}\text{ if }v,w\in V^{\perp}$
$cv\in V^{\perp}\text{ if }v\in V^{\perp}, c\in \mathbb{R}$
$\text{proof) for any }x\in V, x^{T}(v+w)=x^{T}v+x^{T}w=0$
$x^{T}(cv)=cx^{T}v=0$
$\text{(2). }\dim V+ \dim V^{\perp}=n$
$\text{proof) Let }v_{1},v_{2},\ldots,v_{m}\text{ be a basis of V}(m\leq n)$
$\text{Define }A=\begin{bmatrix}v_{1}^{T}\\ v_{2}^{T}\\ \vdots\\ v_{m}^{T}\end{bmatrix} _{m\times n}$
만약 $x\in V^{T}$인 벡터 x를 골랐을 때 $x \perp v_{i} \forall i \Leftrightarrow Ax=0 \Leftrightarrow x\in N(A)$
기존에 $\dim N(A)=n-\text{rank}(A)=n-m$임을 알고 있기 때문에
$\dim N(A)+m = n \Rightarrow \dim V^{T}+\dim V=n (\because \dim N(A)\Leftrightarrow \dim V^{\perp}, rank(A)\Leftrightarrow \dim V)$
$\text{(3). }\mathbb{R}^{n}=V\oplus V^{\perp}$
$\text{meaning for any }x\in \mathbb{R}^{n}\text{, there exist }x_{1}\in V, x_{2}\in V^{\perp}\text{ uniquely such that }x=x_{1}+x_{2}$
(3)번은 $\mathbb{R}^{n}$에 속한 어떤 벡터 x든 $V$와 $V^{\perp}$에 있는 벡터들의 unique한 조합으로 표현할 수 있다는 뜻입니다.
예를 들어, 3차원 공간에서 xy평면인 vector space $V$와 xy평면에 orthogonal한 z축 방향 벡터로 이루어진 vector space $V^{\perp}$이 있다고 생각해보겠습니다.
3차원 공간의 어떤 벡터든 xy평면의 벡터와 z축 방향의 벡터의 조합으로 표현할 수 있습니다.
- uniqueness 증명
$x=x_{1}+x_{2}=y_{1}+y_{2} \text{, where }x_{1},y_{1}\in V, x_{2},y_{2}\in V^{\perp}$
$x_{1}-y_{1}\in V = y_{2}-x_{2}\in V^{\perp}$
왼쪽 벡터는 vector space $V$에 속하고, 오른쪽 벡터는 $V^{\perp}$에 속하므로 둘이 같다는 것이 모순이 되지 않으려면 $x_{1}-y_{1}=0=y_{2}-x_{2}$이어야 합니다. orthogonal한 관계의 vector space가 유일하게 공통으로 가지는 것이 영벡터이기 때문입니다.
$\therefore x_{1}=y_{1}, x_{2}=y_{2}$
마지막으로 앞서 보았던 four fundamental spaces가 orthogonal한 관계이라는 점을 이용해 다음과 같은 정리를 도출해낼 수 있습니다.
$\text{Theorem) }$
$N(A)^{\perp}=C(A^{T})$
$N(A^{T})^{\perp}=C(A)$
$Ax=b \text{ is solvable }\Leftrightarrow b\in C(A) \Leftrightarrow b\perp N(A^{T})$
다음에는 이 orthogonality 개념을 알고, 더 나아간 개념들을 공부할 생각입니다.
'수학 Mathematics > 선형대수학 Linear Algebra' 카테고리의 다른 글
| [응용선형대수] Cosines and Projection onto lines (0) | 2023.07.31 |
|---|---|
| [선형대수학] 행렬 분류 Matrix Phylogeny (0) | 2022.03.20 |
| [응용선형대수] Linear Transformations (0) | 2021.03.05 |
| [응용선형대수] The four fundamental subspaces (0) | 2021.03.04 |
| [응용선형대수] Linear independence, basis and dimensions (0) | 2021.03.02 |