1. Inner products and cosines
cosine의 물리적인 의미는 다음과 같이 이해할 수 있다.
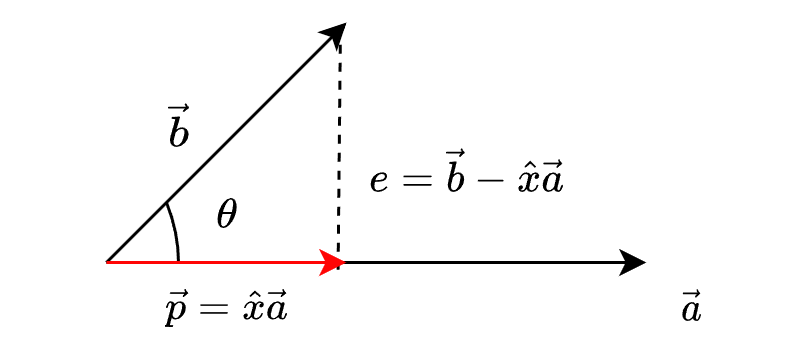
위에서 벡터 b를 a에 대해 projection한 결과 (편의성을 위해 위의 벡터 표시는 생략)
$p=\|b\| \cos\theta \dfrac{a}{\|a\|}=\dfrac{\|a\| \|b\|\cos\theta }{\|a\|^{2}}a=\dfrac{a^{\top}b}{a^{\top}a}a$
첫번째 부등식은 그림을 보고 유도한 것이고 그 다음 등식은 내적과 cosine의 관계를 통해 유도된 것이다.
위를 통해 b를 a에 대해 projection한 결과는 $\dfrac{a^{\top}b}{a^{\top}a}$ 관계로 연결되어있음을 확인할 수 있다.
그러나 위의 결과는 2차원 평면에서 유도하는 결과이기 때문에 좀 더 general하게 보여주면 다음과 같다.
$a^{\top}(b-\hat{x}a)=a^{\top}b-\hat{x}a^{\top}a=0 \quad \because a\perp (b-\hat{x}a)=0$
$a^{\top}b=\hat{x}a^{\top}a$
$\hat{x}=\dfrac{a^{\top}b}{a^{\top}a}$
이렇게도 증명할 수 있다.
2. Schwartz inequality
이와 관련해서 벡터 상에서의 schwartz inequality (한국 발음으로는 슈바르츠 inequality)를 보일 수 있다.
$\text{Schwartz inequality : }|a^{\top}b| \leq \|a\|\|b\|$
이 부등식을 증명하는 방법은 2가지가 있는데
1) 첫번째로는 정석적으로 $|\cos\theta |\leq 1$이라는 점을 이용하는 것이다.
$|a^{\top}b|=\|a\|\|b\|\cos\theta $라는 점을 이용하면 $|\cos\theta |\leq 1$이므로 위 부등식이 성립한다.
그런데 이 증명방식은 제한적이라고 들었다. 왜 제한적인지는 더 높은 수학 상위 개념을 많이 몰라서 그런 것인데 추측건대 4차원만 되어도 각도라는 개념을 우리가 쉽게 정의하기 어렵다. 그래서 수직(orthogonality)에 대해서 이야기할 때도 처음에는 2차원 평면 그림으로 이해를 하지만 실제 정의를 보면 각도와 무관하게 정의된다. 따라서 더 높은 차원으로 이야기할 때는 명료하면서도 일반적인 서술을 통해 증명하는 듯하다.
2) $\left\| b-\dfrac{a^{\top}b}{a^{\top}a}a\right\|^{2}\geq 0$이라는 점을 이용해서 증명한다.
$\left( b^{\top}-\dfrac{a^{\top}b}{a^{\top}a}a^{\top} \right) \left( b-\dfrac{a^{\top}b}{a^{\top}a}a \right)$
위 식을 전개하면
$b^{\top}b-2\dfrac{a^{\top}b}{a^{\top}a}a^{\top}b+\dfrac{(a^{\top}b)^{2}}{a^{\top}a}\geq 0$
$\dfrac{\|b\|^{2}a^{\top}a-(a^{\top}b)^{2}}{a^{\top}a}\geq 0 \quad \Leftrightarrow \|a\|^{2}\|b\|^{2}\geq(a^{\top}b)^{2}$
3. Projection matrix
앞서서 보인 식은
$p=\dfrac{a^{\top}b}{a^{\top}a}a$이라는 식이었는데 역으로 b에 대한 식으로 나타내보자.
$p=Pb \quad \text{where }P : \text{projection matrix}$
$p=\dfrac{1}{a^{\top}a}(a^{\top}b)a=\dfrac{1}{a^{\top}a}a(a^{\top}b)=\dfrac{aa^{\top}}{a^{\top}a}b$
$P=\dfrac{aa^{\top}}{a^{\top}a}$
이 matrix는 특정 벡터를 a 벡터에 projection 시키는 matrix이고 rank가 1이다. (동일한 벡터를 가지고 matrix를 만들면 rank가 1이 될 수 밖에 없다.) 분모로 들어가는 $a^{\top}a$는 스칼라이므로 사실 상 matrix를 normalize하는 역할을 한다.
몇 가지 properties
1) $P^{\top}=P$
2) $P^{2}=P$ : 한 번 projection 시키면 또 projection 시켜도 같은 결과가 나온다.
4. Transpose와 Inner product의 관계
$(Ax)^{\top}y=(x^{\top}A^{\top})y=x^{\top}(A^{\top}y)$
이 관계를 통해 $(Ax,y)=(x,A^{\top}y)$임을 알 수 있다.
즉, $B=A^{\top} \text{ if }(Ax,y)=(x,By) \; \forall x,y$
'수학 Mathematics > 선형대수학 Linear Algebra' 카테고리의 다른 글
| [응용선형대수] Orthonormal bases and Gram-schmidt (0) | 2023.12.28 |
|---|---|
| [선형대수학] 행렬 분류 Matrix Phylogeny (0) | 2022.03.20 |
| [응용선형대수] Orthogonal vectors and subspace (0) | 2021.03.06 |
| [응용선형대수] Linear Transformations (0) | 2021.03.05 |
| [응용선형대수] The four fundamental subspaces (0) | 2021.03.04 |