
선형대수학에서 여러 matrix category가 있는데 맨날 정의를 잊어버리고 각 개념의 포함관계를 잘 알 수 없었다.
그래서 책(아래 참고문헌 적어놓음)을 참고하여 이번에 정리를 하고자 한다.
첫 번째 분류
1. Square / Non-square matrix
matrix의 행과 열의 길이가 같으면 square matrix라고 한다.
그렇지 않은 non-square matrix는 선형대수학을 공부하면서 거의 다루지 않지만 dynamics를 공부하다보면 흔하게 나온다.
일반적인 경우에 변수와 방정식의 갯수가 일치하기가 쉽지 않기 때문이다. 그래서 이런 non-square matrix도 분석할 수 있는 Singular Value Decomposition(SVD)를 수행할 수 있다. SVD는 square matrix의 eigenvalue decomposition과 동일하다.
아래 분류는 Square matrix에 집중한다.
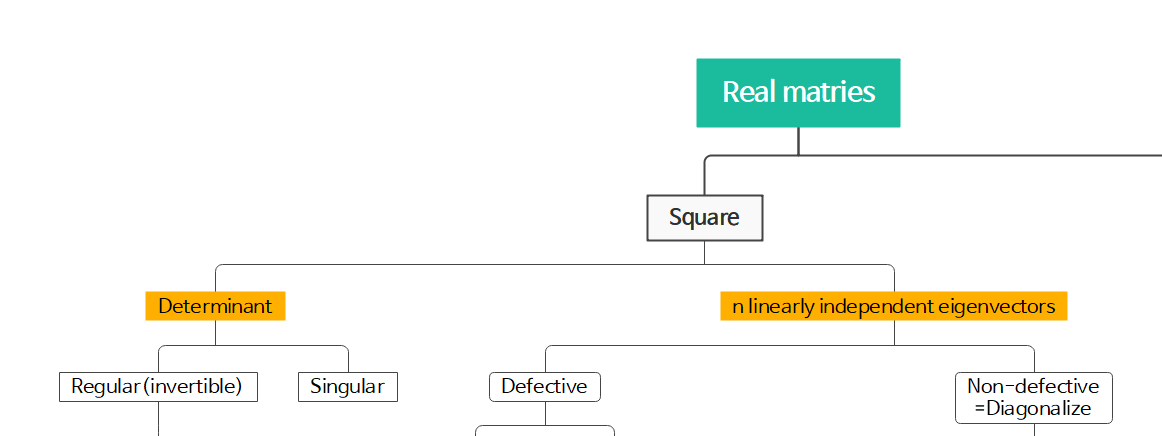
두 번째 분류 기준
2. Determinant
Determinant는 square matrix를 하나의 스칼라로 바꿔주는 연산자라고 볼 수 있다. matrix의 크기에 따라 다르지만 일반적으로 2x2 matrix는
$\det \begin{bmatrix}a&b\\c&d\end{bmatrix}=ad-bc$
라고 알려져있다.
이 determinant가 0이면 singular matrix라고 한다.
그리고 determinant가 0이 아니면 regular matrix, invertible matrix라고 한다. 또는 nonsingular matrix라고도 할 수 있을 것이다. invertible matrix라는 이름에서 알 수 있듯이 이 matrix는 역행렬 계산이 가능하다.
또한 같은 square matrix 분류 중에서도 다른 기준이 있다.
3. n linearly independent eigenvectors
matrix를 eigenvalue decomposition을 했을 때 선형독립인 eigenvectors가 matrix의 차원인 n개만큼 존재하는지 아닌지에 따라 나눌 수 있다.
Non-detective matrix는 diagonalizable matrix와 같다. 즉, n개의 선형 독립 eigenvectors를 가졌다는 뜻이다.
반대로 defective matrix는 diagonalizable하지 않다. 즉, 대각화 행렬로 바꿀 수 없다. eigenvalue decomposition의 목적 중 하나는 어떤 matrix를 eigenvectors의 상수 곱으로 표현할 수 있도록 대각화하는 게 목적이기 때문에 이렇게 분류를 한 것으로 보인다. defective matrix에는 repeated eigenvalue를 가진 경우와 complex eigenvalue를 가진 경우가 포함될 수 있다. repeated eigenvalue를 가진 경우에는 jordan form으로 대각 행렬과 비슷하게 바꿀 수 있고, complex eigenvalue인 경우에는 실수부와 허수부를 분리하여 대각 행렬과 비슷하게 바꿀 수 있다.
참고로 eigenvalue 중에 0이 있는 경우는 2번의 determinant 기준으로 봤을 때 singular matrix인 경우이다.
$Ax=0$을 만족시키는 eigenvector가 있을 수 있다. 따라서 2번 분류 기준과 3번 분류 기준이 어떤 집합에 속해있는 게 아니라 별개로 생각하는 것이다.
$\text{Example : }A=\begin{bmatrix}1&0 \\ 0 & 0 \end{bmatrix}$
$\text{eigenvalue : }1,0$
$(A-1\cdot I)v_{1} =\begin{bmatrix}0&0 \\ 0 & -1 \end{bmatrix}v_{1}=\begin{bmatrix}0 \\ 0 \end{bmatrix} \Rightarrow v_{1}=\begin{bmatrix}1 \\ 0 \end{bmatrix}$
$(A-0\cdot I)v_{2}=\begin{bmatrix}1&0 \\ 0 & 0 \end{bmatrix}v_{2}=\begin{bmatrix}0 \\ 0 \end{bmatrix} \Rightarrow v_{2}=\begin{bmatrix}0 \\ 1 \end{bmatrix}$
$\textbf{Definition. (defective matrix) }\text{A square matrix }A\in \mathbb{R}^{n\times n}\text{ is defective if it possesses}$
$\text{fewer than n linearly independent eigenvectors.}$
$\textbf{Algebraic multiplicity :}$
Let a square matrix $\boldsymbol{A}$ have an eigenvalue $\lambda_{i}$. The algebraic multiplicity of $\lambda_{i}$ is the number of times the root appears in the characteristic polynomial.
eigenvalue decomposition을 할 때 $\det (A-\lambda I)$를 구할 때 그 eigenvalue가 여러 번 곱해져 있는 경우를 algebraic multiplicity가 1보다 큰 경우이다.
$\textbf{Geometric multiplicity :}$
Let $\lambda_{i}$ be an eigenvalue of a square matrix $\boldsymbol{A}$. Then the geometric multiplicity of $\lambda_{i}$ is the number of linearly independent eigenvectors associated with $\lambda_{i}$. In other words, it is the dimensionality of the eigenspace spanned by the eigenvectors associated with $\lambda_{i}$.
한 eigenvalue에 대해서 선형 독립인 eigenvector가 여러 개 존재하는 경우 geometric multiplicty가 1보다 크다.
이제 Regular matrix에서 좀 더 분류를 할 생각이다.

Regular matrix = invertible matrix = singular matrix 중에서
orthogonal eigenvectors를 가지면 orthogonal matrix라고 한다.
orthogonal eigenvectors는 각 eigenvectors의 내적이 0이라는 뜻이다.
$\textbf{Definition. (orthogonal matrix) }\text{A square matrix }A\in \mathbb{R}^{n\times n }$
$\text{is an orthogonal matrix if and only if its columns are orthonormal so that }$
$AA^{\top}=I=A^{\top}A \Rightarrow A^{-1}=A^{\top}$
이것이 complex domain으로 확장되면 Unitary matrix라고 한다.

Non-defective matrix에 대해서 분류를 해보면
n개의 선형독립인 eigenvectors를 가지고 있을 때
$A^{\top}A=AA^{\top}$이 성립하면 normal matrix라고 한다. 그렇지 않으면 non-normal matrix.
그런데 이 $A^{\top}A$가 Identity matrix이면 위에서 다뤘던 orthogonal matirx라고 볼 수 있다.
normal matrix 중에는 symmetric matrix (complex domain까지 포함하면 Hermitian matrix)가 있다. symmetric matrix는 분류기준으로 보았을 때 항상 n개의 선형독립인 eigenvectors가 존재하며, eigenvalues는 항상 real이다.
또한 symmetric matrix 안에 속하는 positive definite matrix는 모든 eigenvalue가 0보다 큰 matrix로, cholesky decomposition을 할 때 unique한 결과가 나오는 것이 알려져있다.
즉, positive definite matrix는 항상 symmetric이다.
사실 엄밀히 따지면 positive definite의 정의는 다음과 같다.
$v^{\top}Av>0 \text{ for real }v\neq 0$을 만족하는 symmetric matrix를 positive definite라고 한다.
$A=\begin{bmatrix}1 & 1 \\ -1 & 1\end{bmatrix}$인 경우에는 $v^{\top}Av>0$이지만 이 때는 eigenvalue가 complex number이라는 점이 중요하다. 이렇게 positive definite임을 알고 싶은 이유는 보통 최적화 문제에서 다루는 경우인데 그 때 결과인 $v$가 complex이길 바라지 않기 때문에 애초에 symmetric이라는 가정을 달아놓는 것 같다.
한편 Hermitian matrix 중에서도 $v^{*}Av>0 \text{ for complex }v\neq 0$을 만족하면 positive definite라고 한다.
참고문헌
Deisenroth, Marc Peter, A. Aldo Faisal, and Cheng Soon Ong. Mathematics for machine learning. Cambridge University Press, 2020.
'수학 Mathematics > 선형대수학 Linear Algebra' 카테고리의 다른 글
| [응용선형대수] Orthonormal bases and Gram-schmidt (0) | 2023.12.28 |
|---|---|
| [응용선형대수] Cosines and Projection onto lines (0) | 2023.07.31 |
| [응용선형대수] Orthogonal vectors and subspace (0) | 2021.03.06 |
| [응용선형대수] Linear Transformations (0) | 2021.03.05 |
| [응용선형대수] The four fundamental subspaces (0) | 2021.03.04 |