우리가 제어를 할 때 actuator model을 넣는 것이 현실적이다. 비행기의 control surface를 제어하는 경우에는 이 control surface를 제어하는 물리적인 장치가 신호 전달에 개입하기 때문이다.
보통 actuator는 1차 시스템, 또는 2차 시스템으로 모델링하는데 여기서는 왜 1차 시스템으로 모델링하는지에 대해
책에서 이에 대한 설명을 봐서 소개하고자 한다. 더 좋은 actuator model에 대한 설명이 있으면 추가할 예정이다.
여기서는 electric motor를 기준으로 모델링을 한다.
모터는 입력 전압에 비례하게 torque를 발생시킨다. 이를 수식으로 표현하면
$T_{m}=k_{m}v_{c}$
$\text{where } v_{c} \text{ : voltage, }T_{m}\text{ : torque, }k_{m}\text{ : proportional constant}$
그리고 모터 축의 각도($\theta$)와 torque의 관계는 물리적으로 정해져있다.
$I\ddot{\theta}=T_{m}$
I는 moment of inertia, 회전 관성이다.
위의 두 식을 합쳐서 입력 전압에 대한 모터의 회전 각도를 알 수 있다.
$\frac{\theta}{v_{c}}=\frac{k_{m}}{Is^{2}}$
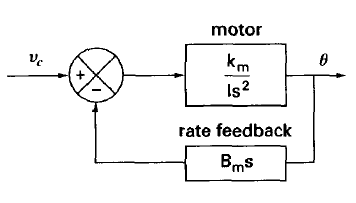
그런데 시스템 상으로 모터에 입력을 넣는다고 해서 open loop로 무작정 전압을 넣지는 않는다.
원하는 입력 전압에 대한 각도를 표현하기 위해 각도에 대한 rate feedback, 즉 각도 변화율을 피드백하는 루프로 closed loop 제어를 한다. (위 그림 참고)
이 경우에는 각도와 입력 전압의 관계는 다음과 같이 표현할 수 있다.
$\frac{\theta}{v_{c}}=\frac{k}{s(\tau_{m}s+1)}$
$\text{where }\tau_{m}=\frac{I}{k_{m}B_{m}}\text{ and }k=\frac{1}{B_{m}}$
이 식을 보면 입력에 대한 각도 결과로, transfer function의 분모의 order가 2차인 것을 확인할 수 있다. 즉, 이 경우에는 actuator를 2차로 모델링한 것처럼 볼 수 있다.
만약 $\tau_{m}$이 충분히 작다면 1차 식처럼 근사시킬 수 있다.
$\frac{\theta}{v_{c}}=\frac{k}{s}$

앞선 경우가 rate feedback을 한 것이라면, 위 그림처럼 position feedback을 이용해서 모터를 제어할 수도 있다. 이 경우에 각도와 입력 전압의 관계는 다음과 같이 나온다.
$\frac{\delta_{f}}{v_{c}}=\frac{k}{\tau s+1}$
$\text{where }k=\frac{1}{k_{f}}\text{ and }\tau=\frac{B_{m}}{k_{f}k_{a}}$
이 식을 보면 transfer function이 1차로 나타난 것을 알 수 있다.
즉, 일반적인 actuator model이 1차 또는 2차로 표현되는 이유는 위와 같은 모델링을 기반으로 이뤄지는 것이다.
실제로는 실험 등을 통해서 모터의 데이터를 알고, 그 데이터에 맞게 모델링할 수도 있다고 한다.
참고문헌
Robert C. Nelson, Flight Stability and Automatic Control
'연구 Research > 제어 Control' 카테고리의 다른 글
| [제어] Realization에 대한 고찰 (0) | 2022.04.16 |
|---|---|
| [제어] Transfer function을 s plane에 mapping하는 코드 (0) | 2022.04.11 |
| [제어] H2 norm, H infinity norm 개념 (0) | 2021.11.30 |
| [제어] Control theory 관련 레퍼런스 정리 (1) | 2021.11.11 |
| [고등자동제어] Singular Value Decomposition과 Degree of Controllability (0) | 2021.02.26 |