시스템에 대한 Transfer function을 구하면 보통 $s=j\omega$로 두고 bode plot을 그려서 주파수 응답을 확인한다.
bode plot 외에도 nyquist plot, nichols plot 등 시스템에 대해 이해하기 위한 plot들이 있다.
그런 plot은 이미 MATLAB에 구현되어있으므로 넘어가고
여기서 소개하는 코드는 간단하게 직접 s plane(complex domain)에서 Transfer function의 크기와 위상이 어떻게 되는지 확인하는 plot을 그리는 코드이다.
아래 코드에서 사용된 transfer function은
$\frac{s+2}{s^2+6s+5}$
이다.
% Code for magnitude and phase plot of transfer function in s plane
num = [1,2] ;
den = [1,6,5] ;
G = tf(num, den) ;
%G = ( s + 2 )/( s^2 + 6*s + 5 ) ;
pole_sys = pole(G);
real_range = -20:0.1:0 ;
imag_range = -20:0.1:20 ;
n = length(real_range);
m = length(imag_range);
[x,y] = meshgrid(real_range, imag_range) ;
mag = zeros(n,m) ;
phase = zeros(n,m) ;
for i = 1:length(real_range)
for j = 1:length(imag_range)
complex_num = real_range(i)+ 1j*imag_range(j);
g = ( complex_num + 2 )/( complex_num^2 + 6*complex_num + 5 ) ;
mag(i,j) = abs( g ) ;
phase(i,j) = atan2( imag(g), real(g) ) ;
end
end
mag_dB = 20 * log(mag);
phase_deg = 180/pi * phase ;
figure ;
s = surf(y,x,mag_dB') ;
title('Magnitude plot of G(s)') ;
zlabel('Magnitude (dB)');
ylabel('Real');
xlabel('Imaginary');
s.EdgeColor = 'none';
figure ;
s = surf(y,x,phase_deg') ;
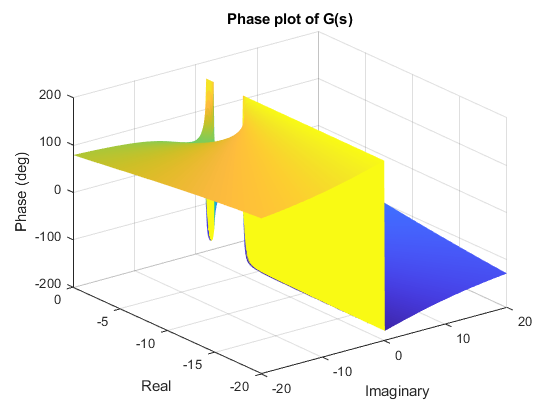
title('Phase plot of G(s)') ;
zlabel('Phase (deg)');
ylabel('Real');
xlabel('Imaginary');
s.EdgeColor = 'none';
이 코드를 좀 더 개선해서 일반화된 transfer function을 plot해주는 함수를 만들면 좋을 것 같다.
NOTE : 누군가는 이 코드를 symbolic 식을 이용해서 subs를 가지고 대입하면 될 것이라고 생각할 수 있는데, 절대 권하지 않는 방식이다. MATLAB 코드를 짤 때 반복적으로 대입(subs)하는 코드는 무조건 속도가 느리다.
위 코드의 결과는 다음과 같다.

'연구 Research > 제어 Control' 카테고리의 다른 글
| [제어] MATLAB을 활용한 Realization (0) | 2022.04.16 |
|---|---|
| [제어] Realization에 대한 고찰 (0) | 2022.04.16 |
| [제어] Actuator modelling (0) | 2021.12.16 |
| [제어] H2 norm, H infinity norm 개념 (0) | 2021.11.30 |
| [제어] Control theory 관련 레퍼런스 정리 (1) | 2021.11.11 |