1. Time domain에서의 해석
low pass filter 식으로 알려져있는 $\displaystyle\frac{y}{y_{c}}=\frac{1}{\tau s + 1}$는
time domain에서 다음과 같이 표현된다.
$\dot{y}+\displaystyle\frac{1}{\tau}(y-y_{c})=0$
여기서 $\tau$는 시상수(time constant)라는 이름으로 많이 쓰인다.
그 의미는, response가 1을 기준으로 $1-e^{-1}=0.6321$만큼 도달했을 때의 시간을 의미한다.
이를 구하는 방법은 역라플라스 변환도 있는데 직접적으로 구하면
$\dot{y}+\displaystyle\frac{1}{\tau}(y-y_{c})=0$
$\displaystyle\frac{dy}{y-y_{c}}=-\frac{1}{\tau}dt$
$\ln\left(\displaystyle\frac{y-y_{c}}{y_{0}-y_{c}}\right)=-\frac{1}{\tau}(t-t_{0})$
$y-y_{c}=-y_{c}e^{-\frac{1}{\tau}t} \; \because y_{0},t_{0}=0$
$y=y_{c}\left(1-e^{-\frac{1}{\tau}t}\right)$
다음과 같이 t가 무한대로 갈 때 $y$가 $y_{c}$에 근사해가는 것을 확인할 수 있다.
이 때 t가 시상수 $\tau$일 때 $1-e^{-1}=0.6321$이 되는 것이다.
내가 도달하고자 하는 $y_{c}$의 63.21%에 도달하는 시간이라고 볼 수 있다.

$y_{c}=10$으로 설정했을 때 다음과 같다.
확대해서 보면 다음과 같다. 검은 점선은 63.21%에 도달한 것을 표시한다.
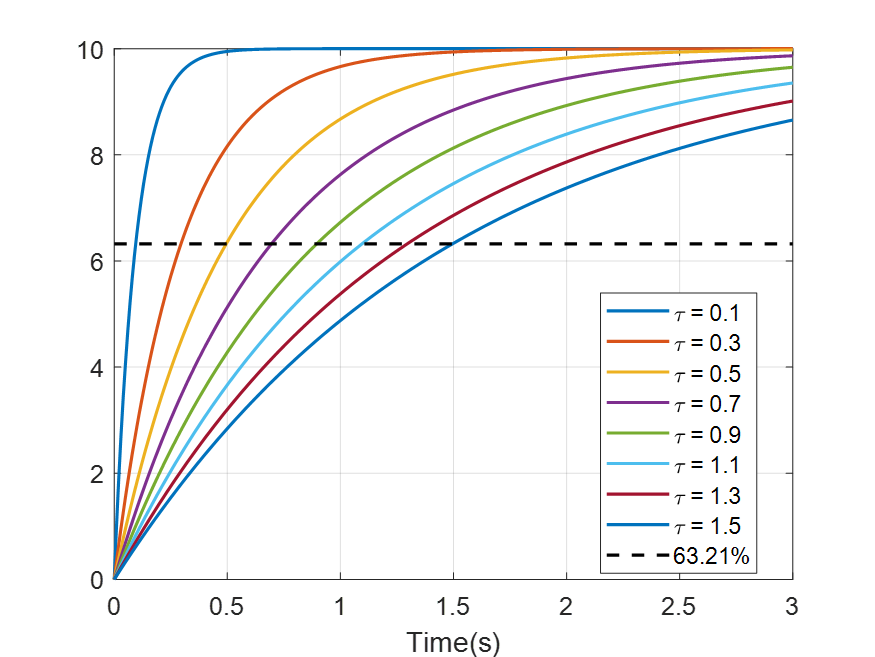
(아래에 이 그래프를 그리는 코드를 첨부했습니다. 참고할 분들은 참고하세요.)
2. Frequency domain에서의 해석
$\displaystyle\frac{y}{y_{c}}=\frac{1}{\tau s + 1}$식은 다른 방식으로도 쓰인다.
위키피디아에는
$\displaystyle\frac{\omega_{0}}{s+\omega_{0}}$과 같이 식으로 표현한다. 그리고 이 $\omega_{0}$는 cutoff frequency라고 한다.
이를 위의 형식에 맞게 변형하면
$\displaystyle \frac{1}{s/\omega_{0}+1}$
위의 $\tau = \displaystyle \frac{1}{\omega_{0}}$ 둘은 일치한다.
$\tau$는 앞서 말한 것처럼 시상수로, dimension이 시간이므로, s(second)이다.
$\omega_{0}$는 rad/s이므로 역수를 취하면 s/rad이므로 둘의 단위가 일치한다. (rad은 no dimension이다.)
그래서 $\tau$를 역수로 취함으로써 frequency domain에서의 cutoff frequency를 알 수 있다.
이 값은 gain이 -3.01dB일 때의 주파수이다.
-3.01dB는 dB가 $20\log_{10}(\text{magnitude})$일 때 magnitude가 0.707를 의미한다.
즉 $20\log_{10}(0.707)=-3.01(dB)$이다.
아래 그래프에서는 $\tau$를 바꿔가며 확인한 것이다.
첫번째 그래프는 frequency가 log scale로 되어있어서 각 cutoff frequency($\omega_{0})$에서 -3.01dB가 됨을 확인할 수 있다.

두번째 그래프는 log scale 대신 일반 scale로 표현한 것이므로, magnitude가 0.707일 때 각각 cutoff frequency에 해당한다는 것을 확인할 수 있다.

이 그림을 그리는 코드 역시 아래에 남겨놓았다.
3. MATLAB 코드
1) Time domain
t_f = 3 ;
dt = 0.01 ;
t = 0:dt:t_f ;
N = floor(t_f/dt) ;
tau = 0.1 * [1:2:15] ;
y_c = 10 ;
figure ;
for k = 1:length(tau)
y = zeros(N+1,1) ;
for i = 1:N
y(i+1) = y(i) - 1/tau(k) * dt * ( y(i) - y_c ) ;
end
plot(t, y, 'DisplayName',"\tau = "+string(tau(k))) ;
hold on ;
end
plot(t, 6.321 * ones(length(t),1), '--k', 'DisplayName','63.21%');
legend('Location','best') ; xlabel('Time(s)');
2) Frequency domain
close all ;
tau = 0.1 * [1, 2, 5, 10] ;
figure(1) ;
figure(2) ;
for k = 1:length(tau)
tf_low_pass = tf([1],[tau(k),1]) ;
[mag, phase, wout] = bode(tf_low_pass, {0.1,20}) ;
figure(1);
plot(wout, squeeze(mag), 'DisplayName',"\tau = "+string(tau(k))+" \omega_{0}="+string(1/tau(k))) ;
hold on ;
figure(2);
semilogx(wout, 20*log10(squeeze(mag)), 'DisplayName',"\tau = "+string(tau(k))+" \omega_{0}="+string(1/tau(k))) ;
hold on ;
end
figure(1) ;
plot(wout, 0.707 * ones(length(wout),1), '--k', 'DisplayName','mag = 0.707');
legend('Location','best') ; xlabel('Frequency(rad/s)'); ylabel('Gain');
figure(2) ;
semilogx(wout, -3.01 * ones(length(wout),1), '--k', 'DisplayName','mag = -3.01(dB)');
grid on ;
legend('Location','best') ; xlabel('Frequency logscale(rad/s)'); ylabel('Gain(dB)');'연구 Research > 제어 Control' 카테고리의 다른 글
| [MATLAB] 3차원 vector field diagram과 시뮬레이션 결과 mapping (0) | 2022.09.26 |
|---|---|
| [제어] Phase portrait 프로그램과 예시 (0) | 2022.09.16 |
| [Optimal Control] Optimal control problem의 performance index (0) | 2022.07.29 |
| [제어] Regulation problem과 Tracking problem (0) | 2022.06.05 |
| [제어] MATLAB을 활용한 Realization (0) | 2022.04.16 |