저번 글에서 phase plane과 vector field diagram을 그려주는 MATLAB app을 소개했었다.
그런데 이 프로그램은 2차원에서만 가능하기 때문에 변수가 하나 더 늘면 구현이 불가능했다.
그래서 간단하게 3차원 공간에서 벡터 필드를 그리고, 실제 초기 조건에 대하여 시뮬레이션까지 수행하여서 그려보는 코드를 작성하였다.
1. 시스템
$\dot{x}=-x+y$
$\dot{y}=-0.1x^3-y-10\sin x$
$\dot{z}=y-z$
다음과 같은 시스템이 있다고 할 때
interval = pi/2 ;
start_pt = -pi ;
end_pt = -start_pt ;
[x1,y1,z1] = meshgrid(start_pt:interval:end_pt, start_pt:interval:end_pt, start_pt:interval:end_pt );위와 같이 mapping할 구간을 정해준다. $[-\pi,\pi]$를 $\pi/2$ 간격으로 구한다.
그리고 위의 시스템 식을 코드 맨 아래에 다음과 같이 정의해준다.
function f = system(t, state)
x = state(1) ;
y = state(2) ;
z = state(3) ;
dx = -x + y ;
dy = -0.1 * x^3 - y - 10*sin(x) ;
dz = y - z ;
f = [ dx ; dy ; dz ] ;
end
시스템이라는 함수는 시간과 state값을 받아서 변화율을 되돌려주는 함수이다. 여기서 함수의 argument 중 시간값을 포함한 이유는 시뮬레이션을 위해서이다. (뒤에서 나온다.)
2. Vector field 계산
이제 각 점에 대한 vector값을 계산한다. x,y,z에 대한 변화율을 u,v,w라는 변수라고 생각하고 구한다.
u = zeros(size(x1));
v = zeros(size(y1));
w = zeros(size(z1));
t = 0 ;
for i = 1:numel(x1)
Yprime = system(t, [x1(i); y1(i); z1(i)]);
u(i) = Yprime(1);
v(i) = Yprime(2);
w(i) = Yprime(3);
end
3. 시뮬레이션
시뮬레이션은 매트랩에 내장되어있는 시뮬레이션 함수 ode45를 사용한다. 다른 솔버들도 있지만 ode45가 범용적으로 쓰이기 때문이다.
x0 = [pi/2, pi/2, pi/2] ;
Tmax = 25 ;
func_handle = @system ;
[time, solvec] = ode45(func_handle, [0,Tmax], x0) ;
x0는 초기 state이고, Tmax는 시뮬레이션 하고자하는 최대 시간이다. 시작시간은 0으로 설정하였다. 앞에서 정의했었던 system이라는 함수의 handle을 넘겨주어야 솔버가 계산을 할 수 있다.
4. Plot
이제 구한 값들을 plot할 때이다.
figure ;
quiver3(x1, y1, z1, u, v, w, 'b','LineWidth', 1.0) ;
xlabel('$x$') ;
ylabel('$y$') ;
zlabel('$z$') ;
hold on;
plot3(solvec(:,1), solvec(:,2), solvec(:,3),'r') ;
plot3(solvec(1,1), solvec(1,2), solvec(1,3),'k*') ;각 축은 x,y,z 이름을 붙였다. 기본 interpreter를 LaTeX로 해놔서 $$를 붙여서 표현했다.
시작점은 검은색 마커로 표시했다.
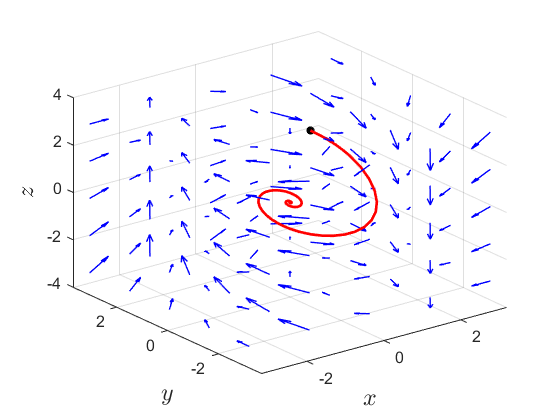
결과는 다음과 같다.
참고로 이런 3D plot은
view(90,0)과 같은 코드를 추가하여 어떤 각도에서 바라볼지 정할 수 있다.
view_array = [90,0 ; 0,0 ; 0,90] ;
for i = 1:3
figure ;
quiver3(x1,y1,z1,u,v,w, 'b','LineWidth', 1.0) ;
xlabel('$x$') ;
ylabel('$y$') ;
zlabel('$z$') ;
hold on;
plot3(solvec(:,1),solvec(:,2),solvec(:,3),'r') ;
plot3(solvec(1,1),solvec(1,2),solvec(1,3),'k*') ;
view(view_array(i,1), view_array(i,2)) ;
end
다음과 같이 반복문을 통해서 view가 (90,0)일 때, (0,0)일 때, (0,90)일 때를 plot할 수 있다.
여기서 view 안에 들어가는 숫자는 좌표축에 대한 카메라 시선의 방위각과 고도각을 의미한다.
1) view(90,0) : 방위각 90도, 고도각 0도라는 말은 x축 상에서 바라보는 그림이 된다.

2) view(0,0) : 방위각 0도, 고도각 0도. 이 때는 y축 상에서 바라본다.

3) view(0,90) : 방위각 0도, 고도각 90도라는 말은 z축 상에서 바라본다는 의미이다.

'연구 Research > 제어 Control' 카테고리의 다른 글
| [제어] eigenvalue와 stability 분석 (algebraic multiplicity와 geometric multiplicity의 차이) (0) | 2022.12.14 |
|---|---|
| [제어] Lyapunov stability theorem 증명 (0) | 2022.09.29 |
| [제어] Phase portrait 프로그램과 예시 (0) | 2022.09.16 |
| Low pass filter에서 시상수(Time constant)의 의미 (0) | 2022.08.16 |
| [Optimal Control] Optimal control problem의 performance index (0) | 2022.07.29 |