Autonomous 시스템에 대하여 Phase portrait (state plane, phase plane)을 그려주는 프로그램이 있어서 수업시간에 배운 내용을 그려보았다.
프로그램의 UI가 잘 되어있어서 추천하는 바이다.
1. Tunnel-diode circuit system
다음 시스템은 Tunnel-diode circuit 시스템을 다룬 것이며 이 시스템은
$x_{1}=v_{C}, x_{2}=i_{L}$ 일 때
$$
\begin{gathered}
\dot{x}_1=0.5\left[-h\left(x_1\right)+x_2\right] \\
\dot{x}_2=0.2\left(-x_1-1.5 x_2+1.2\right) \\
h\left(x_1\right)=17.76 x_1-103.79 x_1^2+229.62 x_1^3-226.31 x_1^4+83.72 x_1^5
\end{gathered}
$$
으로 표현된다.
이 시스템은 비선형 시스템이기 때문에 분석에 어려움이 있다. 일반적으로 비선형 시스템은 평형점에서 선형화를 하여서 분석을 한다.
이 시스템의 평형점은 총 3개가 나온다.
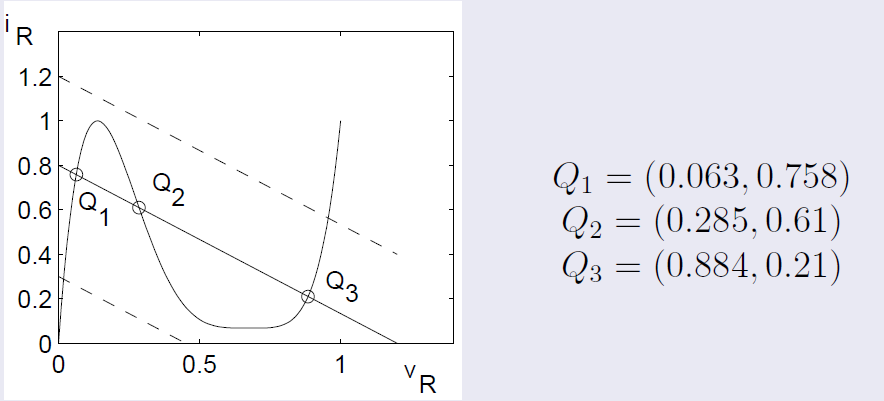
위 그림은 Khalil 교수님의 수업자료에서 가져온 것이다.
평형점은 총 3개이고 안정성 분석을 위해서 선형화를 통해 살펴보아야한다.
아래 수식을 통해 알 수 있듯이 각 Q1,Q2,Q3에 해당하는 선형화된 A matrix를 보면 Q1, Q3는 안정(stable)하고 Q2는 saddle point이다.
$$
\begin{aligned}
\frac{\partial f}{\partial x}=\left[\begin{array}{cc}
-0.5 h^{\prime}\left(x_1\right) & 0.5 \\
-0.2 & -0.3
\end{array}\right] \\
A_1=\left[\begin{array}{cc}
-3.598 & 0.5 \\
-0.2 & -0.3
\end{array}\right], \quad \text { Eigenvalues : }-3.57,-0.33 \\
A_2=\left[\begin{array}{cc}
1.82 & 0.5 \\
-0.2 & -0.3
\end{array}\right], \quad \text { Eigenvalues : } 1.77,-0.25 \\
A_3=\left[\begin{array}{cc}
-1.427 & 0.5 \\
-0.2 & -0.3
\end{array}\right], \quad \text { Eigenvalues : }-1.33,-0.4
\end{aligned}
$$
이를 시각화해서 나타내면 다음과 같다.

이 글에서 소개하고자 하는 phase portrait를 통해서 이 점들을 살펴보면 안정한 평형점인지를 다시 확인할 수 있다.

그림을 클릭하면 확대해서 볼 수 있다.
다양한 initial point에 대하여 시뮬레이션을 돌려보았을 때
Q2에서 시작한 점은 Q2에서 머물리지 않고 Q1으로 수렴한다. 조금만 빗겨나가면 Q3로 수렴할 것이다.
Q2를 기점으로 양 옆에서는 두 개의 평형점으로 갈라져서 수렴이 진행된다.
2. Van der Pol Oscillator
Nonlinear dynamical system에서 볼 수 있는 몇 가지 행동 중 하나는 Limit cycle이다.
limit cycle은 phase portrait에서 시간이 양의 방향 또는 음의 방향으로 무한대로 갈 때, 1개 이상의 닫혀있는 궤적 위에 존재하는 것을 말한다. 개별 state로 보면 oscillation하는 것처럼 보인다.
limt cycle도 stable, unstable, semi-stable limit cycle로 나뉘는데 stable limit cycle은 시간이 양의 방향으로 흐를 때 limit cycle을 형성하는 것이고, unstable limit cycle은 시간이 음의 방향으로 흐를 때 limit cycle을 형성하는 것이다. 이 말을 달리 말하면, limit cycle 위에서 시작할 때 시간이 흐르면 그 limit cycle을 벗어나게 된다는 뜻이다.
semi-stable limit cycle은 어떤 구간에서는 시간의 양의 방향으로 갈 때 limit cycle, 어떤 구간에서는 음의 방향으로 갈 때 limit cycle이면 semi-stable이라고 한다. 즉, 어떤 곳에서 시작하면 stable limit cycle처럼 동작하고, 다른 경우에는 unstable limit cycle처럼 동작하는 것이다.
이 예시에서 다루는 Van der Pol Oscillator는 stable limit cycle의 대표적인 예이다.
$\dot{x}_{1} = x_{2}$
$\dot{x}_{2}=-x_{1}+\mu(1-x_{1}^{2})x_{2}$

이 식에서는 $\mu$ 값에 따라서 limit cycle의 형태가 달라진다.
이와 같이 비선형 시스템 특성을 확인하기 위해 phase portrait을 확인해볼 수 있다.
참고자료
https://kr.mathworks.com/matlabcentral/fileexchange/61636-pplane
Pplane
An updated version of Pplane that works on Matlab R2018b
kr.mathworks.com
'연구 Research > 제어 Control' 카테고리의 다른 글
| [제어] Lyapunov stability theorem 증명 (0) | 2022.09.29 |
|---|---|
| [MATLAB] 3차원 vector field diagram과 시뮬레이션 결과 mapping (0) | 2022.09.26 |
| Low pass filter에서 시상수(Time constant)의 의미 (0) | 2022.08.16 |
| [Optimal Control] Optimal control problem의 performance index (0) | 2022.07.29 |
| [제어] Regulation problem과 Tracking problem (0) | 2022.06.05 |