Chap2. Analytic Functions
Sec 13. Functions and Mappings
S : a set of complex numbers
function f defined on S : rule that assigns to each z in S a complex number $\omega$
이 때의 set S를 domain of definition이라고 합니다.
\omega : value of f at z $\Rightarrow \omega=f(z)$
function에는 그 domain of definition과 value를 구하는 rule이 잘 정의되어 있어야 합니다.
$u+iv = f(x+iy)$이라고 할 때 x,y에 대한 real valued function의 pair로 표현할 수 있습니다.
$f(z)=u(x,y)+iv(x,y)$
$u+iv = f(re^{i\theta})$
$f(z)=u(r,\theta)+iv(r,\theta)$로도 표현할 수 있습니다.
일반적으로 real valued function은 한 평면 위의 그래프로 그릴 수 있는데, $w=f(z)$와 같은 complex valued function의 경우에는 f의 graphical representation을 한 평면에 나타낼 수 없습니다. 왜냐하면 $z=(x,y)$와 $w=(u,v)$ 모두 line이 아니라 plane이기 때문입니다. 즉, plane에서 plane으로 mapping해야하는 상황입니다.
이렇게 $z$에 대응되는 $w$ plane의 관계를 보여주는 function f를 mapping이라고도 표현합니다.
$\text{The image of a point in the domain of definition S : point of }w=f(z)$
S 안에 속한 set T에 있는 point들에 대한 image는 the image of T라고 합니다.
$\text{The range of f : the image of the entire domain of definition of S}$
$\text{The inverse image of a point }\omega \text{ is the set of all points }z\text{ in the domain of definition of f}$
inverse image가 none at all인 경우는, $w$가 range of f에 속하지 않은 경우입니다.
mapping이라는 개념은 dominant geometric characteristics of certain mappings을 보았을 때, 이미지의 translation, rotation, reflection 등으로 표현할 수도 있습니다.
(실제 게임 개발할 때 사용하는 유니티에서 쿼터니언 등의 복소수 개념을 쓴다고 들었는데 복소수 계산을 통해 이미지를 mapping하는 게 아닐까 싶습니다.)
예를 들어
- tranlation : $w = z+1=(x+1)+iy$ : 실수 축 방향으로 1만큼 평행이동한 것으로 해석할 수 있습니다.
- rotation : $w = iz=r\exp[i(\theta+\frac{\pi}{2})]$ : 각도를 clockwise로 $\frac{\pi}{2}$만큼 회전한 것으로 해석할 수 있습니다.
- reflection in real axis : $w = \bar{z}=x-iy $ : y값이 부호가 바뀌었으므로 일종에 실수축에 대해 반사시킨 것으로 해석할 수 있습니다.
Sec 14. The mapping $w= z^{2}$
이 책에서는 mapping 중에서도 $f(z)=z^{2}$의 예시만을 다룹니다. 예전 edition에서는 더 많은 사례를 다룬 것 같은데 독자들이 $w=z^{2}$만 사용해도 된다고 제안을 했다고 합니다. (preface에서)
$w=z^{2}$의 경우에 $z=x+iy$일 때 $u(x,y)=x^{2}-y^{2},v(x,y)=2xy$가 나옵니다.
이제 이 mapping에서의 특정 case들을 통해 mapping 특징을 알아낼 수 있습니다.
1) $u=x^{2}-y^{2}=c_{1}\text{, where }c_{1}>0$

$x^{2}-y^{2}=c_{1}$는 z plane에서는 쌍곡선(hyperbola)을 의미합니다. z plane에서는 쌍곡선인 z가 w plane에서는 $u=c_{1}$인 상수함수가 됩니다.
이 때 image의 direction이 중요합니다. z plane에서 오른쪽 쌍곡선을 보면 화살표가 위로 갈수록, 즉, y값이 증가할수록 그 점에 대응되는 w plane의 점도 imaginary axis를 따라 위로 올라갑니다.
반대로 왼쪽 쌍곡선에서는 아래로 갈수록, 즉, y값이 감소할수록 그 점에 대응되는 w plane의 점도 imaginary axis를 따라 위로 올라갑니다.
2) $v=2xy=c_{2}\text{, where }c_{2}>0$

$v=c_{2}$일 때는 분수함수가 z plane에 그려지고($y=\frac{c_{2}}{2x}$), 이에 대응되는 것은 w plane의 $v=c_{2}$라는 상수함수입니다. 제1사분면에 있는 z plane의 그래프에서 x값이 0에서 무한대로 갈수록, w plane의 상수함수도 real axis 축을 따라 무한으로 가는 것을 알 수 있습니다.
제3사분면에 있는 z plane 그래프는 x가 음의 무한대로 갈수록, y가 0에 가까워질수록 w plane의 point는 무한으로 갑니다.
또한 더 생각해볼 것이 있습니다.
2)번과 같이 $v=2xy=c$ case에서 c를 바꿔가면서 확인해보는 것입니다.
예를 들어 c값이 커질수록 x,y축에서 멀어진다는 것은 다들 아실 겁니다. c가 0에 가까울 때부터 무한대까지 바꾼다면 그 그래프가 차지하는 면적은 z plane의 제1사분면입니다. 이 값들을 w plane에 mapping한다면, 역시 0에 가까운 곳에서부터 무한대($v\sim 0 \rightarrow \infty$)까지 mapping되므로 w plane의 제1사분면, 제2사분면을 mapping하게 됩니다.

이 그림이 위의 설명을 가시적으로 보여준 그림입니다. 또한 $c=0$인 경우를 $(0,y)$와 $(x,0)$인 경우로 나눠서 w plane에서 $v=0=c,u<0$, $v=0,u>0$으로 mapping될 수 있음을 보여주었습니다.
따라서 $w=z^{2}$ mapping은 z plane의 제1사분면을 w plane의 제 1,2사분면으로 mapping한 것으로 이해할 수 있습니다.
이는 polar coordinate 관점의 mapping으로도 이해할 수 있습니다.

$z=re^{i\theta}$일 때 $w=r^{2}e^{i2\theta}$입니다.
z plane의 제1사분면은 $0<\theta<\frac{\pi}{2}(\Rightarrow \text{First quadarant})$이고
w plane에 mapping된 결과는 $0<2\theta<\pi(\Rightarrow \text{Upper half plane})$입니다.
이를 확장해서 $w=z^{n}=r^{n}e^{in\theta}$를 이해할 수 있습니다.
w plane의 한 nonzero point에 대해 대응되는 z plane의 distinct point가 n개가 된다는 뜻입니다.(앞서 배운 roots of complex numbers와 연관지어도 이해할 수 있습니다. n에 대한 root는 $c_{o}\omega_{n}^{k}$에서 $k=0,\ldots,n-1$까지 n개가 있기 때문입니다.)
위의 $w=z^{2}$로 나타낸 위의 예시에도, 같은 w값에 대해 대응되는 곡선 위의 점 2개가 있었습니다.
추가)
$w=z^{2}$ mapping에서
$u=c_{1}\text{, where }c_{1}<0$인 경우와
$v=c_{2}\text{, where }c_{2}<0$인 경우를 풀어보았습니다.

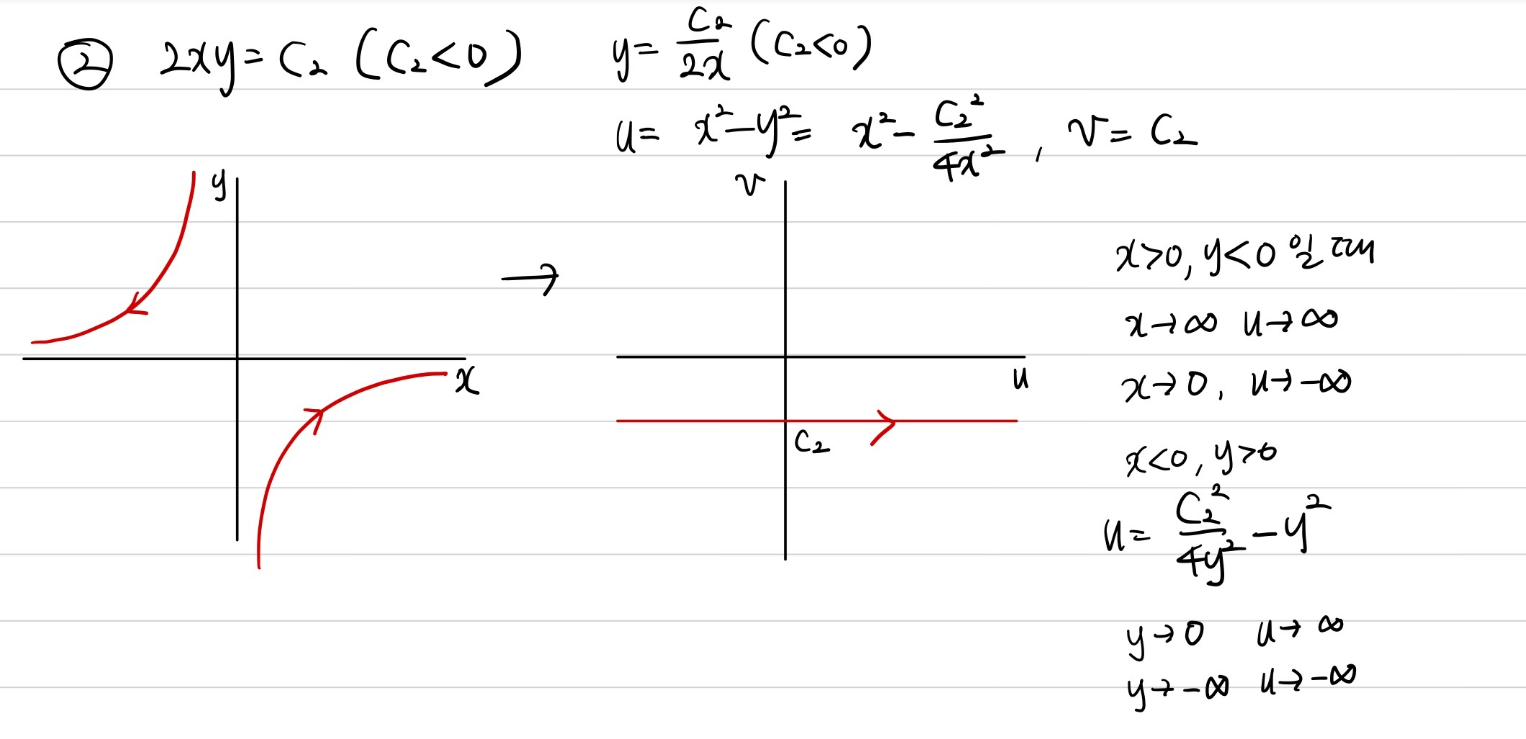
여기서 할 수 있는 흥미로운 사실은 z plane의 제2사분면을 w plane에 mapping하면 lower half plane이 되고,
z plane의 $\frac{\pi}{4}\geq \theta\geq \frac{3\pi}{4}$
w plaen의 left half plane으로 mapping됩니다.
'수학 Mathematics > 복소해석학 Complex Analysis' 카테고리의 다른 글
| [응용복소함수] Chap2 : Cauchy-Riemann equations (0) | 2021.03.08 |
|---|---|
| [응용복소함수] Chap2 : Derivatives (0) | 2021.03.07 |
| [응용복소함수] Chap2 : Limits, Continuity (0) | 2021.03.05 |
| [응용복소함수] Chap1 : Complex numbers (0) | 2021.03.04 |