Sec 15. Limits
앞서 배웠던 neighborhood와 mapping은 limit를 정의할 때 필요한 부분이었습니다. complex plane에서 정의된 function에 대한 limit에 대해 알아보겠습니다.
function $f$는 a point $z_{0}$의 some deleted neigborhood 안에 속한 모든 points $z$에 대해 정의되어있습니다.
$f(z)$가 가진 limit는 다음과 같이 표현합니다.
$\underset{z\rightarrow z_{0}}{\lim}f(z)=w_{0}$
이에 대한 자세한 의미는 아래와 같습니다.
$\text{for positive number }\varepsilon\text{, there is a positive number }\delta\text{ such that }$
$|f(z)-w_{0}|<\varepsilon \text{ whenever }0<|z-z_{0}|<\delta$

$\text{for each }\varepsilon\text{ neighborhood }|w-w_{0}|<\varepsilon\text{ of }w_{0}\text{, there is a deleted }\delta\text{ neighborhood }$
$0<|z-z_{0}|<\delta \text{ of }z_{0}\text{ such that every point z in it has an image w lying in the }\varepsilon \text{ neighborhood}$
그림과 함께 이해를 해보면, $z_{0}$의 $\delta$ deleted neighborhood 안에 속한 모든 $z$가 $w_{0}$의 $\varepsilon$ neighborhood를 image로 가지는 $\delta$가 존재한다는 뜻입니다.
여기서 주목할 점은, '모든' $\delta$ deleted neighborhood 안의 $z$는 $w_{0}$의 $\varepsilon$ neighborhood 안에 속해있어야 한다는 점입니다. 하지만 반드시 z가 $\varepsilon$ neighborhood 안을 모두 채울 필요는 없습니다.
$\text{Theorem) }$
$\text{When a limit of a function }f(z)\text{ exists at a point }z_{0}\text{, it is unique.}$
$\text{Proof) }$
$\underset{z\rightarrow z_{0}}{\lim}f(z)=w_{0} \text{ and }\underset{z\rightarrow z_{0}}{\lim}f(z)=w_{1}$이라고 가정하자.
positive number $\varepsilon$에 대해서
$|f(z)-w_{0}|<\varepsilon \text{ whenever }0<|z-z_{0}|<\delta_{0}$
$|f(z)-w_{1}|<\varepsilon \text{ whenever }0<|z-z_{0}|<\delta_{1}$
을 만족하는 positive number $\delta_{0},\delta_{1}$가 존재합니다.
$w_{1}-w_{0}=[f(z)-w_{0}]+[w_{1}-f(z)]$
다음과 같은 표현식을 알고, triangle inequality를 적용하면,
$w_{1}-w_{0}\leq [f(z)-w_{0}]+[w_{1}-f(z)]=|f(z)-w_{0}|+|f(z)-w_{1}|$
만약 $0<|z-z_{0}|<\delta \text{ where }\delta\text{ is any positive number smaller than }\delta_{0}\text{ and }\delta_{1}$일 때
$|w_{1}-w_{0}|\leq \varepsilon+\varepsilon = 2\varepsilon$
$\epsilon$을 아주 작은 값으로 잡는다면 $w_{1}-w_{0}=0$이므로 $w_{1}=w_{0}$
즉, limit 값은 unique합니다.
$\text{Example) }$
$f(z)=\frac{z}{\bar{z}}$의 원점에서의 limit를 구해봅시다.
limit를 구할 때는 '어떤 방향이든지' 같은 결과가 나와야합니다.
만약 real-axis 방향으로 limit를 한다면 $z=(x,0)$일 때
$\underset{x\rightarrow 0}{\lim} f(z)=\frac{x}{x}=1$
imaginary-axis 방향으로 limit를 한다면 $z=(0,y)$
$\underset{y\rightarrow 0}{\lim} f(z)=\frac{iy}{-iy}=-1$
두 방향의 limit 값이 다르므로 unique하지 않고, 위의 theorem에 의해 이 함수는 $\underset{z\rightarrow 0}{\lim}f(z)\text{ does not exist}$
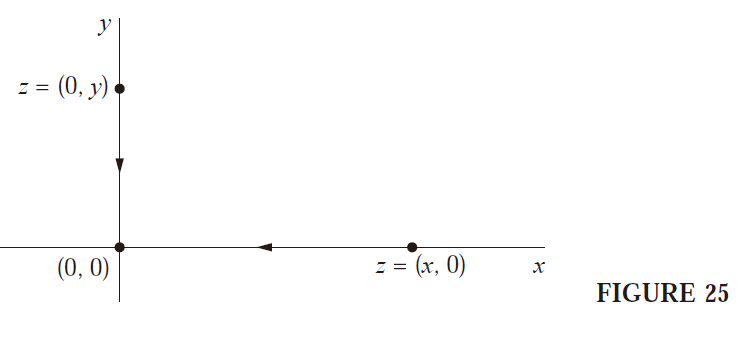
그런데 위에서 다룬 limit의 definition은 주어진 $w_{0}$\ 점이 limit인지 아닌지 테스트하는 데에 의미가 있지, limit를 정하는 방법은 알 수가 없습니다. 그래서 다음 section에서는 limit를 찾는 방법에 대해서 공부합니다.
Sec 16. Theorems on Limits
complex valued function의 limits은 real-valued functions of two real variables의 limits와 연관이 되어있습니다.
$\text{Theorem 1.}$
$\text{Suppose that} f(z)=u(x,y)+iv(x,y) (z=x+iy)\text{ and }z_{0}=x_{0}+iy_{0}, w_{0}=u_{0}+iv_{0}$
$\underset{(x,y)\rightarrow(x_{0},y_{0})}{\lim} u(x,y)=u_{0} \text{ and }\underset{(x,y)\rightarrow(x_{0},y_{0})}{\lim} v(x,y)=v_{0}\cdots (1)$
$\text{Then, }\underset{z\rightarrow z_{0}}{\lim} f(z)=w_{0}\cdots (2)$
$\text{and, conversely, if statement (2) is true, then so is statement (1).}$
이 theorem의 의의는 real-valued functions of two real variabls의 limits로 complex valued function의 limit를 알 수 있다는 점입니다. 역으로 complex valued function의 limit를 알고 있으면 real-valued functions of two real variables의 limits를 알 수 있습니다.
그리고 개별적인 function의 limit와 그 function들의 조합으로 이루어진 function의 limit의 관계에 대한 theorem이 있습니다.
$\text{Theorem 2. Suppose that }$
$\underset{z\rightarrow z_{0}}{\lim}f(z)=w_{0}\text{ and }\underset{z\rightarrow z_{0}}{\lim} F(z)=W_{0}$
$\text{Then, }$
$\underset{z\rightarrow z_{0}}{\lim}[f(z)+F(z)]=w_{0}+W_{0}$
$\underset{z\rightarrow z_{0}}{\lim}[f(z)F(z)]=w_{0}W_{0}$
$\text{and, if }W_{0}\neq 0,$
$\underset{z\rightarrow z_{0}}{\lim}[\frac{f(z)}{F(z)}=\frac{w_{0}}{W_{0}}$
이 theorem을 통해 바로 알 수 있는 성질들
$\underset{z\rightarrow z_{0}}{\lim}z^{n}=z_{0}^{n}$ $(n=1,2,\ldots)$
$\text{limit of Polynomial }P(z)=a_{0}+a_{1}z+a_{2}z^{2}+\cdots+a_{n}z^{n}$
$\underset{z\rightarrow z_{0}}{\lim}P(z)=P(z_{0})$
Sec 17. Limits Involving the Point at Infinity
real value와 달리 complex value는 음의 무한대가 없고 무한대만 있습니다. 또한 complex plane은 일직선이 아닌 2차원 공간이므로 무한대를 정의하는 방법이 real value와 다릅니다.

point at infinity를 포함하는 complex plane을 extended complex plane이라고 합니다. 이 complex plane이 적도면을 지나가도록 하는 unit sphere가 있습니다. complex plane 위에 놓인 점 z에 대해서 sphere의 north N을 잇는 line을 만듭니다. 이 line과 sphere가 만나는 교점을 P라고 합니다. N은 point at infinity라고 정해줌으로써, P와 extended complex plane에 놓인 z는 일대일 대응(one to one correspondence)이 됩니다. (이 sphere를 Riemann sphere, 이 correspondence를 stereographic projection라고 합니다.)
z가 원점에서 아주 멀리 멀어질수록(즉 무한으로 갈수록) 점 P는 north N(=point at infinity)로 다가갑니다.
다른 limit는 일반적으로 대응되는 값이 $z\varepsilon$ neighborhood 안에 들어와야 하지만 역으로 무한대로 가는 극한값은 위에서 나온 무한대의 정의처럼 특정 범위보다 z값이 커야한다고 볼 수 있습니다.
$|z|>\frac{1}{\varepsilon}\text{ : a neighborhood of }\infty$
이렇게 $\infty$의 neighborhood를 정의하는 이유는, 무한대에 대한 극한값을 증명할 때 neighborhood를 알아야 하기 때문입니다.
$\text{Theorem) }$
$\text{If }z_{0}\text{ and }w_{0} \text{ are pointsin the z and w planes, respectively, then }$
$\underset{z\rightarrow z_{0}}{\lim} f(z)=\infty \text{ if }\underset{z\rightarrow z_{0}}{\lim}\frac{1}{f(z)}=0$
$\underset{z\rightarrow \infty}{\lim} f(z)=w_{0}\text{ if }\underset{z\rightarrow 0}{\lim}f(\frac{1}{z})=w_{0}$
$\underset{z\rightarrow \infty}{\lim} f(z)=\infty \text{ if }\underset{z\rightarrow 0}\frac{1}{f(1/z)}=0$
Sec 18. Continuity
$\text{A function f is continous at a point }z_{0}\text{ if all three of the following conditions are satisfied : }$
$(1). \underset{z\rightarrow z_{0}}{\lim} f(z)\text{ exists,}$
$(2). f(z_{0})\text{ exists,}$
$(3). \underset{z\rightarrow z_{0}}{\lim} f(z)=f(z_{0})$
(3)이 곧 (1),(2)를 포함하는 말이며, (3)은 곧
$|f(z)-f(z_{0})|<\varepsilon \text{ whenever }|z-z_{0}|<\delta$
또한
A function of a complex variable is said to be continuous in a region R if it is continuous at each point in R
$\Rightarrow$ 특정 region에서 continuous하기 위해서는 region R 안에 있는 각 점에 대해서 모두 continuous여야 합니다.
$\text{Theorem 1. A composition of continuous functions is itself continuous.}$
두 continuous한 함수 두 개를 합성한 함수도 continuous합니다.
$\text{Theorem 2. If a function }f(z)\text{ is continuous and nonzero at a point }z_{0},$
$\text{then }f(z)\neq 0\text{ throughout some neighborhood of that point.}$
$f(z_{0})\neq 0$인 continuous한 함수 $f(z)$가 있을 때 0을 포함하지 않는 $z_{0}$의 neighborhood가 조내합니다.
$f(z)=u(x,y)+iv(x,y)$라고 할 때,
$\text{Theorem 3. If the component functions u and v are continuous at a point }z_{0}=(x_{0},y_{0})\text{, then so is f. }$
$\text{Conversely, if f is continuous at }z_{0}\text{, the same is ture of u and v at that point.}$
이전에서 다룬 것을 통해 complex-valued function의 limit와 두 real-valued functions of two real variables의 limit는 연관성이 있다는 점을 알고 있습니다.
비슷하게, $u,v$가 $(x_{0},y_{0})\leftarrow z_{0}$에 대해서 continuous할 때 f 역시 continuous합니다.
$\text{Theorem 4. If a function f is continuous throughout a region R that is both closed and bounded,}$
$\text{there exists a nonnegative real number M such that } |f(z)|\leq M\text{ for all points z in R,}$
$\text{where equality holds for at least one such z.}$
bounded, closed region R에서 continuous하다면 f(z) is bounded on R이라고 표현할 수 있습니다.
'수학 Mathematics > 복소해석학 Complex Analysis' 카테고리의 다른 글
| [응용복소함수] Chap2 : Cauchy-Riemann equations (0) | 2021.03.08 |
|---|---|
| [응용복소함수] Chap2 : Derivatives (0) | 2021.03.07 |
| [응용복소함수] Chap2 : Function, Mapping (0) | 2021.03.04 |
| [응용복소함수] Chap1 : Complex numbers (0) | 2021.03.04 |