(이 글의 자료들은 모두 교재에서 나온 것이므로, 다른 곳으로 가져가지 말아주세요)
우리가 고체역학에서 다루는 문제, 그리고 시스템은 비록 부피와 질량이 있지만, 부피와 질량을 고려할 필요가 없는 상황에서는 물체를 particle로 생각하고 그 particle에 대한 force와 moment를 구해서 계산하는 것이 더 편리합니다.
a particle 하나에 여러 힘이 작용할 때 그 힘과 동일하게 작용하는 힘을 resultant force라고 합니다.
resultant force를 구하는 것은 물체의 평형(equilibrium)을 따질 때 도움이 됩니다.
1. Force
force는 point of application, magnitude, line of action, 그리고 sense로 특정할 수 있습니다.
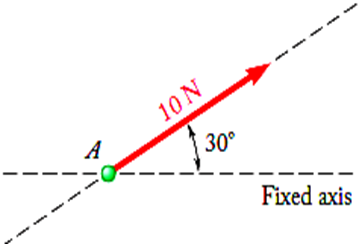
다음과 같은 force가 있을 때 A가 point of application(작용점), 그리고 10N이 magnitude, force가 작용하는 선을 무한하게 늘린 것이 line of action입니다. line of action(작용선)은 fixed axis와 어떤 각도를 가지고 있는지로 정해질 수 있습니다. 또한 sense는 화살표가 가리키는 방향입니다.
아래 그림은 위의 그림과 같은 line of action, magnitude를 가졌지만 sense가 다른 예시입니다.
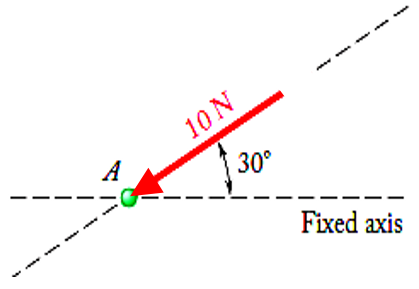
또한 force에 대한 설명에서 알 수 있는 것처럼 force는 vector라고 할 수 있습니다.
2. Vector
물리량 중에서는 scalar, vector, tensor,... 등으로 분류할 수 있습니다.
scalar는 magnitude을 가지고 방향은 없는 물리량입니다. 예를 들면, mass, volume, temperature가 있습니다.
vector는 scalar와 같이 magnitude가 있으면서 direction을 가지고 있는 물리량입니다.
고등학교 때 물리를 배우면 속도와 속력의 차이에 대해서 배우는데, 속도가 벡터이고 속력은 스칼라입니다.
displacement(변위), velocity(속도), acceleration(가속도) 모두 벡터입니다.
또한 vector도 분류를 할 수 있습니다. (나중에 고체역학의 많은 내용을 이해하는데에 중요한 내용입니다.)
- Fixed or bound vectors : defined points of application(정해진 작용점)이 있어서 문제 조건을 바꾸지 않는 이상 바뀔 수 없는 vectors
- Free vectors : 공간에서 자유롭게 움직일 수 있는 vectors를 free vectors라고 합니다.
- Sliding vectors : lines of action을 따라서 움직일 수 있는 vectors를 sliding vectors라고 합니다.
2.1. Additive of vectors
vector의 합은 다들 익숙한 것처럼, 평행사변형을 그려서 구하는 방법(Trapezoid rule) 또는 삼각형을 그려서 구하는 방법(Triangle rule) 중 하나를 사용하면 됩니다.
$\overrightarrow{R}=\overrightarrow{P}+\overrightarrow{Q}=\overrightarrow{Q}+\overrightarrow{P}$ (commutative)
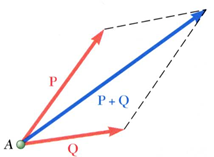

벡터의 각도를 구하기 위해서 코사인 법칙이나, 사인 법칙을 이용할 수도 있습니다.
$\text{Law of cosine : }c^{2}=a^{2}+b^{2}-2ab\cos C$
$\text{Law of sine : }\frac{\sin A}{a}=\frac{\sin B}{b}=\frac{\sin C}{c}$
vector의 substraction은 additive의 변형입니다.
$\overrightarrow{R}=\overrightarrow{P}-\overrightarrow{Q}=\overrightarrow{P}+(-\overrightarrow{Q})$

2.2. Concurrent forces

동일한 point에 작용하는 forces들의 집합 (set of forces which all pass through the same point)
한 점에 작용하는 concurrent forces는 a single resultant force로 표현할 수 있고, 이 resultant force는 작용한 힘들의 vector sum입니다.
2.3. Rectangular components of force : Unit vectors
2.2. 파트에서 같은 점에 작용하는 여러 개의 힘들을 하나의 Resultant force로 나타낼 수 있다고 했습니다. 이를 역으로 생각하면 하나의 Resultant force를 다른 힘들로 분해할 수 있다는 뜻도 됩니다.
따라서 우리는 고정된 축에서 force를 해석하기 위해 특정 force vector를 수직한 벡터 components로 분해할 수 있습니다.
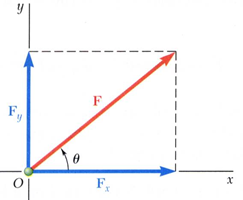
위의 그림에서 $\vec{F}=\vec{F_{x}}-\vec{F_{y}}$로 분해한 것을 볼 수 있습니다.
만약 이 수직한 x축과 y축에 대해 unit vector $\vec{i},\vec{j}$로 정의한다면

$\vec{F}=\vec{F_{x}}-\vec{F_{y}}$를 더 나아가서
$\vec{F}=F_{x}\vec{i}+F_{y}\vec{j}$
각 unit vector를 scaling한 다음에 합한 것으로 볼 수 있습니다.
이 수직한 unit vector들은 내적이나 외적을 할 때 유리한 측면이 있기 때문에 이렇게 표현하는 방법도 배우게 됩니다.
그래서 resultant force를 구할 때도 concurrent force의 x component와 y component의 합으로 구할 수 있습니다.




만약 이 점에서 equilibrium of a particle이면 $R_{x}=0, R_{y}=0$입니다.
2.4. Expressing a vector in 3D space
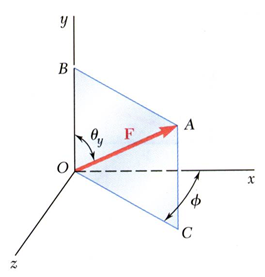
다음과 같은 3차원 벡터가 있을 때는 $\vec{F}$와 y축 사이의 각도 $\theta_{y}$, F를 xz 평면에 projection한 다음에 x축과 이루는 각도 $\phi$를 알고 있으면 쉽게 분해할 수 있습니다.

$F_{y}=F\cos \theta_{y}$
$F_{x}=F\sin \theta_{y} \cos \phi$
$F_{z}=F\sin \theta_{y} \sin \phi$
또는 이렇게 하는 것이 아니라 아예 F와 동일한 방향의 단위 벡터를 구해서 표현할 수도 있습니다.

$\vec{F}$가 x,y,z축과 $\theta_{x},\theta_{y},\theta_{z}$ 각도를 가지고 있을 때
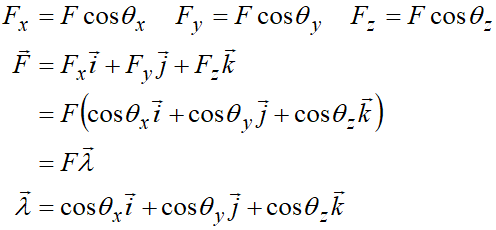
다음과 같이 표현할 수 있습니다.
꼭 $\theta_{x,y,z}$를 알지 못하더라도 각 좌표를 알고 있으면 길이 비를 이용해서 cosine값을 알 수 있으므로 유용한 방법입니다.
다음에는 force와 moment에 대해서 자세히 다루도록 하겠습니다.
'기계공학 Mechanical engineering > 고체역학 Statics & Solid mechanics' 카테고리의 다른 글
| [고체역학] Statics Ch5 : Centroids and Centers of Gravity (0) | 2021.04.27 |
|---|---|
| [고체역학] Statics Ch4 : Equilibrium of Rigid Bodies (0) | 2021.04.25 |
| [고체역학] Statics Ch3 : Rigid Bodies (2) Moment of a Couple (0) | 2021.04.25 |
| [고체역학] Statics Ch3 : Rigid Bodies (1) Equivalent Systems of Forces (0) | 2021.04.25 |
| [고체역학] Introduction (1) | 2021.03.28 |
