이전에는 particle에 대해 힘을 분석하는 작업을 했는데 모든 상황에서 particle로 생각할 수는 없습니다.
이번에는 부피와 질량을 가진 물체에 대해서 힘이 작용할 때 그 힘을 다른 방식으로 표현하는 방법에 대해서 배웁니다.
1. External and Internal forces
외부 힘과 내부 힘을 구별해야 하는 이유는 시스템을 free body diagram으로 분석할 때 내부 힘은 무시하고 외부 힘만 표시해야하기 때문입니다. 내부 힘은 어차피 작용 반작용에 의해서 사라질 힘이기 때문에 신경 쓸 필요가 없습니다.

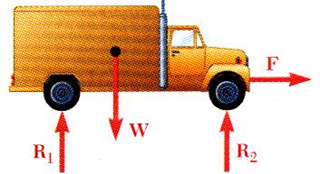
다음과 같이 외부에서 사람이 잡아당기는 차에 대해서 free body diagram을 그리려고 한다고 하겠습니다.
차에 대해서 시스템을 분석할 때, 만약 차 안에 있는 운전자가 차를 밀고 있다고 해도, 운전자가 차에 가하는 힘은 어차피 차가 운전자에 가하는 힘과 동일하기 때문에 굳이 고려하지 않아도 됩니다.
위 그림에서 차에 작용하는 외부 힘은 바깥에 있는 세 명의 사람들이 잡아당기는 힘, 그리고 각 바퀴에 걸리는 수직항력과 중력 뿐입니다.
2. Principle of Transmissibility
어떤 motion이나 평형은 force가 그 힘의 line of action을 따라서 움직인다고 해도 영향을 받지 않습니다.
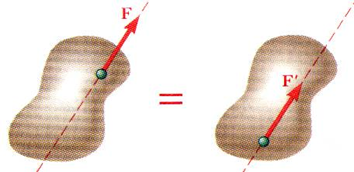
이 그림에서 $\vec{F}$가 line of action에 따라서 조금 움직여서 $\vec{F^{'}}$ 상황이지만 실제 motion에는 영향을 미칮 않습니다.
이 principle의 장점은 우리가 시스템을 묘사할 때 시스템의 운동이 바뀔 걱정 없이 힘의 위치를 바꿀 수 있다는 점입니다.
3. Moment of a Force About a Point
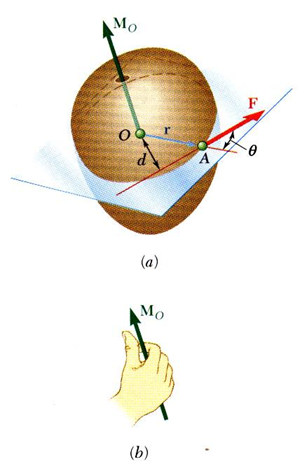
어떤 rigid body에 작용하는 힘은 그 작용하는 점에 따라서 모멘트 역시 작용합니다.
$\text{The moment of F about O : }M_{O}=r\times F$
여기서 $\times$는 vector product(cross product, 외적)으로 외적에 대한 자세한 내용은 맨 아래에 적어놓았습니다.
O점에 대한 force에 의한 moment의 크기는 $rF\sin\theta=Fd$만큼, 방향은 $\vec{r},\vec{F}$에 수직인 방향으로 작용합니다. 결국 이 모멘트는 $M_{O}$의 방향 축을 기준으로 물체가 회전하도록 만듭니다.
또한 위에서 배운 Principle of Transmissibility를 떠올리면 force가 line of action을 따라 움직이는 한, 점 O에서 떨어진 거리 d는 유지되므로 동일한 방향과 크기를 유지하는 모멘트를 발생시킵니다. (즉 동일한 운동을 만듦)
그리고 고체역학에서 주로 two dimensional structure을 다루는데, 이 경우에는 force과 거리 벡터가 모두 xy평면에서 다루므로, 모멘트는 항상 평면에 수직인 벡터로 작용합니다.(z방향 벡터)
* two dimensional structure : length와 breadth만 고려하고 depth는 고려 안 하는 structure. force 역시 평면에서 작용한다.
모멘트 방향을 정의할 때는 counterclockwise 방향을 rotation을 만드는 모멘트가 positive입니다.
반대로 clockwise 방향의 rotation은 negative moment입니다.
4. Varignon's theorem

이 theorem은 점 O에서 작용하는 모멘트를 구할 때, 여러 개의 concurrent force가 있으면 그 concurrent force에 대한 resultant force에 대한 모멘트는 개별 force가 만드는 모멘트를 합친 것과 동일하는 theorem입니다.

이는 vector product의 distributive property를 통해서도 이해할 수 있습니다.
5. Moment of a Force About a Given Axis

$\text{Moment }M_{O}\text{ of a force F applied at the point A about a point O, }\vec{M_{O}}=\vec{r}\times \vec{F}$
이 모멘트를 OL이라는 축에 대해서 구하면, 모멘트 벡터 $M_{O}$를 축 OL에 Projection해야합니다.
$M_{OL}=\vec{\lambda}\cdot \vec{M_{O}}=\vec{\lambda}\cdot (\vec{r}\times \vec{F})$
만약 Cartesian coordinate에 대해서 F의 moment를 구하면 다음과 같습니다. (x,y,z는 force가 작용하는 위치)

배경 지식
1. Vector Product

$\vec{P}\times \vec{Q} = |PQ\sin \theta|$
product 방향은 $\vec{P},\vec{Q}$에 수직인 벡터
1. Not Commutative : $Q \times P = -(P \times Q)$
2. Distributive : $P\times (Q_{1}+Q_{2})=P\times Q_{1}+P \times Q_{2}$
3. Not associative : $(P\times Q)\times S \neq P\times(Q\times S)$
Cartesian coordinate에 대해서

$P\times Q$를 Cartesian vector product에 대해서 해석하면
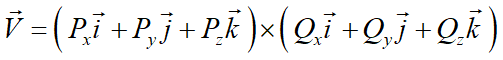


2. Scalar Product

고등학교 때 배운 내적입니다.

또한 어떤 축에 대해 다른 벡터를 projection 시키고 싶다면,


$P_{OL}$이 OL 축을 기준으로 P벡터를 projection시키는 것인데, $\vec{\lambda}$는 OL 축의 단위벡터입니다.
$\vec{\lambda}=\cos\theta_{x} \vec{i}+\cos\theta_{y} \vec{j}+\cos\theta_{z} \vec{k}$
3. Mixed Triple Products

P, Q벡터의 외적을 S 벡터에 대해 내적한다면,

다음과 같은 결과가 나옵니다.
(이것을 배우는 이유는 특정 축에 대한 모멘트를 projection시키기 위함입니다.)
'기계공학 Mechanical engineering > 고체역학 Statics & Solid mechanics' 카테고리의 다른 글
| [고체역학] Statics Ch5 : Centroids and Centers of Gravity (0) | 2021.04.27 |
|---|---|
| [고체역학] Statics Ch4 : Equilibrium of Rigid Bodies (0) | 2021.04.25 |
| [고체역학] Statics Ch3 : Rigid Bodies (2) Moment of a Couple (0) | 2021.04.25 |
| [고체역학] Statics Ch2 : Statics of Particles (0) | 2021.04.04 |
| [고체역학] Introduction (1) | 2021.03.28 |