이 글의 그림 자료 등은 참고 교재가 출처이므로, 다른 곳에 가져가지 말아주세요.
같은 chapter 3의 (1)을 보고 오면 훨씬 이해하기 편합니다.
1. Moment of a Couple
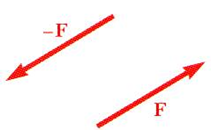
같은 크기, 평행한 lines of action, 반대 방향의 두 force $F$와 $-F$는 couple을 이룬다고 말할 수 있습니다.
이 couple이 만드는 moment를 구해보겠습니다.
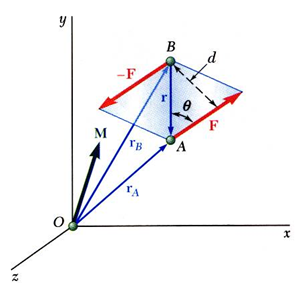
점 O에 대해서 moment를 구하면

이렇게 구한 M은 $\vec{r_{A}},\vec{r_{B}}$에 관계없이 couple을 이루는 force 사이의 거리($d$)와 Force의 크기로 결정되며, 방향은 couple을 이루는 force를 지나는 평면에 대해 수직인 방향입니다.
이렇게 구한 moment vector of the couple은 free vector입니다. 즉, 모멘트의 기준점에 독립적이라는 뜻입니다.
이전 글(normal-engineer.tistory.com/113?category=954778)에서도 언급했듯이 free vector은 공간에서 자유롭게 움직일 수 있습니다.
위에서 moment vector of the couple을 구하는 공식($\vec{r}\times \vec{F}$)에서도 알 수 있듯이 force가 작용하는 위치와 관계없이 모멘트를 구하기 때문에, 원점이 어디든지 상관이 없게 되고 따라서 free vector의 조건을 만족하는 것입니다.

만약 두 couples이 평행한 평면 위에 있고, $F_{1}d_{1}=F_{2}d_{2}$를 만족한다면 두 couples은 동일한 모멘트를 가지게 됩니다. 즉, 같은 rotation을 만드는 영향을 줍니다.
2. Couple vectors
couple이 중요한 이유는 couple에 의해 만들어진 moment가 free vector이고, 따라서 원하는 위치에 옮겨서 해석할 수 있기 때문입니다.

특정 위치에 작용하는 couple은, 하나의 moment vector와 동일한 운동 효과를 만들기 때문에 위 그림에서 두 번째 그림인 couple vector $M$으로 표현할 수 있고, 이 couple vector는 free vector이기 때문에 원점으로 옮겨도 전혀 문제가 되지 않습니다. (free vector는 no point of application, 그저 body에 작용하는 것임)
또한 cartesian coordinate로 해석하고 싶다면, 그 moment를 x,y,z축에 대해서 projection할 수도 있을 것입니다.
여기서 주목할 점은, 한 물체에 작용하는 couple을 하나의 모멘트 벡터로 표현할 수 있다는 것입니다. 이는 rigid body에서 어떤 점에 작용하는 force를 우리가 원하는 위치에 대해서 force와 moment로 표현하고 싶을 때 유용합니다.
3. Resolution of a Force into a Force at O and a Couple
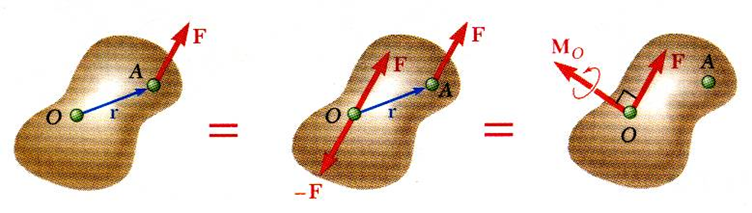
위 그림을 보면 점 A에 force F가 작용하고 있습니다.
우리가 원하는 것은 점 O에 대해서 Force F의 효과를 표현하는 것입니다.
점 O에서 force F와 동일한 힘을 추가하면서 그 힘을 상쇄하기 위해 -F 역시 추가합니다. 이렇게 하면 두 힘의 sum은 0이므로 물체의 운동 자체에는 영향을 미치지 않습니다.
그런데 점 O에 작용하는 -F와 점 A에 작용하는 F는 Couple이므로 couple vector(동일한 효과를 가진 moment vector)로 바꿀 수 있고 free vector이므로 위치를 점 O로 옮기면 맨 오른쪽 그림처럼 나타납니다.
우리가 원하는 대로 점 A에 작용하는 Force F를 점 O에 대해 표현할 수 있게 된 것입니다. 대신 점 A에서 점 O로 옮기는 과정에서 모멘트가 추가되었습니다. 직관적으로 생각해도 점 A에서 힘이 작용하면 rigid body는 변형이 없다면 변위도 분명 발생하겠지만 점 O에 대해서 회전을 시작할 것이고, 그 회전이 모멘트 $M_{O}$으로 표현된다고 생각할 수 있습니다.
이렇게 위 그림의 중간 그림에서 나타난 세 개의 force vector가 동일한 운동 효과를 만드는 equivalent force vector와 couple vector로 나타낼 수 있는데 이를 force-couple system이라고 합니다.
4. Reducing System of Foreces to a Force-Couple System
앞서 배운 내용들을 이용해서 한 rigid body에 작용하는 (각각 다른 point of application을 가진) force를 한 점에 대한 force-couple system으로 만들 수 있습니다.

역으로, 만약에 각각 다른 시스템을 한 점에 대해 동일한 force-couple system으로 reducing되었다면 그 시스템은 개별 force와 moment는 다르더라도 동일한 시스템이라고 볼 수 있습니다.

위 그림을 보면 점 $O$에 작용하는 $M_{O}^{R}$과 force $R$이 있을 때 점 $O^{'}$에 작용하는 $M_{O^{'}}^{R}$과 force $R$은

이 식을 만족할 때 rigid body에 같은 운동을 만들어내는 equivalent system입니다.
5. Further Reduction of a System of Forces
이전에는 여러 force가 rigid body에 작용할 때 한 점에 대해 하나의 모멘트와 힘으로 표현하는 것에 대해서 생각을 했습니다.
여기서 더 나아가면, couple vector와 force가 한 점에 작용할 때 이를 새로운 line of action에서 작용하는 single force로 나타낼 수가 있습니다.
지금까지 한 것은

이 상황을

아래 그림처럼 점 O에 대해서 표현한 것입니다. 이 때 작용하는 모멘트를 $M_{O}^{R}$, force는 $R$가 있습니다.
역으로 force R을 평행이동해서 점 O에서의 동일한 모멘트와 힘 벡터를 만드는 single force를 구할 수 있습니다.

위 그림처럼 점 A에 작용하는 force R로 equivalent system을 만들 수 있습니다.
이 때 조건은 resultant force $R$와 couple vector $M_{O}^{R}$이 Mutually perpendicular해야한다는 점입니다.
둘이 수직이 아니면 $\vec{r}\times \vec{F}=\vec{M_{O}^{R}}$을 만족하는 점을 구할 수 없는 상황이 존재합니다.
(만약에 $\vec{M_{O}^{R}}$가 z성분 외에 x,y 성분이 있고 $\vec{R}$는 xy평면 벡터라고 가정한 다음에 만족하는 거리벡터 $\vec{r}$을 찾으려고 하면 equation 상으로 만족할 수 없는 경우가 생김을 알 수 있습니다.)
cartensian coordinate 기준으로
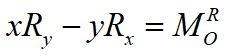
다음을 만족하는 위치 (x,y)가 위의 그림에서의 점 A가 됩니다.
+ mutually perpendicular하게 force-couple system을 만들 수 있는 cases
1) the forces are concurrent
2) the forces are coplanar
3) the forces are parallel
'기계공학 Mechanical engineering > 고체역학 Statics & Solid mechanics' 카테고리의 다른 글
| [고체역학] Statics Ch5 : Centroids and Centers of Gravity (0) | 2021.04.27 |
|---|---|
| [고체역학] Statics Ch4 : Equilibrium of Rigid Bodies (0) | 2021.04.25 |
| [고체역학] Statics Ch3 : Rigid Bodies (1) Equivalent Systems of Forces (0) | 2021.04.25 |
| [고체역학] Statics Ch2 : Statics of Particles (0) | 2021.04.04 |
| [고체역학] Introduction (1) | 2021.03.28 |