물체의 평형에 대해 이해하는 것은 statics에서 아주 중요한 부분입니다.
정역학이라고 번역할 수 있는 statics는 결국 평형을 전제로 물체의 힘과 모멘트를 분석하는 학문이기 때문입니다.
1. Free body diagram
이전에도 free body diagram에 대해서 언급을 했었습니다.
free body diagram은 시스템에 작용하는 모든 외부 힘(external force)를 나타내는 과정입니다.
1. 내가 분석하고자 하는 body가 있으면 그 body를 주변에서 독립시킵니다.
2. 외부 힘의 작용점, 크기, 방향을 생각해서 그립니다. (내부 힘 주의)
3. 특히 작용점과 방향을 표시하는 것이 중요한데, 힘의 방향을 알 수 없는 경우에는 cartensian coordinate에 따라 x,y,z 축 성분을 미지수로 두기로 합니다.
4. moment 계산을 위해서 힘의 크기와 각 작용점 사이의 거리를 표시합니다.

다음과 같은 상황에서 물체에 대해 분석하고자 하면

중력(외부 힘)을 포함해서 위 그림과 같이 free body diagram을 표시할 수 있습니다.
2. Reactions for a Two-dimensional structure
statics에서 주로 나오는 structure에서 힘이 어떻게 작용하는지 미리 알고 있어야 적절한 free body diagram을 그릴 수 있습니다.
기본적으로는 각 structure에서 어떤 자유도가 있는지 파악하고, 자유도가 없을 때 힘과 모멘트가 작용한다고 보면 됩니다. 여기서는 two dimensional일 때를 다룹니다.
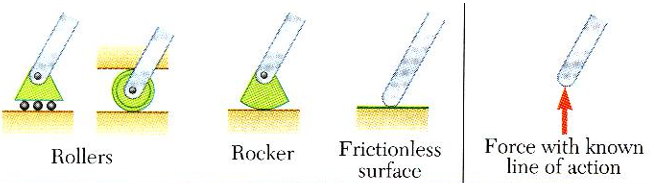
Roller, Rocker, Frictionless surface인 경우 vertical motion은 불가능하고, rotation과 horizontal motion은 가능하지 때문에 수직 방향에 대한 힘만 존재하며, 바닥면에 수직으로 작용합니다.
즉, line of action을 이미 알고 있습니다. line of action을 모를 경우에는 각도를 알 수가 없어서 x축 방향 힘, y축 방향 힘 모두 고려해야 하기 때문에 line of action을 알고 있는지 아닌지가 중요합니다.
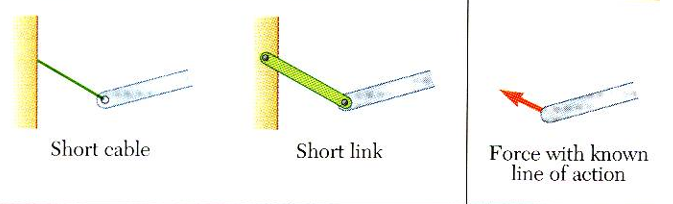
short cable, short link는 cable과 link가 연결된 방향에 대해서 자유롭게 움직일 수 없으므로, 그 방향으로 힘이 작용합니다. 회전은 가능하므로 모멘트는 작용하지 않습니다.

위의 그림 같은 경우에는 rod와 slot 방향을 따라서 자유롭게 움직일 수 있고, rod와 slot의 수직한 방향에 대해서 움직일 수 없으므로 그 쪽 방향에 대해서 힘이 작용하며 회전은 가능하므로 모멘트는 작용하지 않습니다.

frictionless pin이나 hinge, rough surface는 회전이 가능하지만 vertical motion, horizontal motion 둘 다 불가능합니다. 따라서 x,y 축 방향으로 모두 힘이 작용합니다. 문제는 x축 방향의 힘과 y축 방향의 힘 크기를 당장은 알 수 없기 때문에 line of action은 모릅니다.

fixed support는 vertical, horizontal 방향으로 움직일 수 없고 회전도 불가능하므로
x,y 축 방향의 힘은 물론 모멘트도 존재합니다.
3. Apply
이제 equilibrium 개념과 reactions for two-dimensional structure를 free body diagram을 그리는 데 사용해보겠습니다.

다음과 같은 그림을 free body diagram으로 그리려면 어떻게 해야할까요?
기본적으로 빨간색 화살표로 표시된 load는 외부 힘으로 포함해야 할 것입니다
점 E는 fixed support로 보고 x,y축 힘과 모멘트가 외부 힘으로 작용합니다.
여기서 주목할 부분은 D에 대한 해석입니다.
B와 D를 연결하는 cable과 D와 F를 연결하는 cable이 존재합니다. 이 각각의 cable이 D에 작용하는 힘을 외부 힘으로 보느냐, 아니면 cable 역시 시스템에 포함시키느냐에 따라서 free body diagram이 달라질 수 있습니다. 물론 물체에 대한 평형은 바뀌지 않을 테지만 상황에 따라서 편리한 분석이 있을 수는 있습니다.
1) cable에 의해 작용하는 힘을 외부 힘으로 보는 경우

2) cable에 의해 작용하는 힘을 내부 힘으로 보는 경우

그러나 이에 대한 제대로 된 구분 없이 위의 1), 2)를 섞어 쓰면 문제가 됩니다.
또 equilibrium 문제에서는 문제 상황에 따라서 풀 수 있을 수도 있고, 풀 수 없을 수도 있습니다.

다음과 같은 문제에서 P,Q,S가 structure에 작용을 하고 있습니다. 평형을 이루고 있다고 가정하면 이 문제에서 적용할 수 있는 equilibrium equation은

이 세 개입니다. Two dimensional이므로 z축 힘과 x,y 축 모멘트를 고려할 필요가 없기 때문입니다.
다만 equilbrium equation을
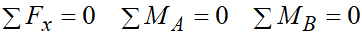
이렇게 점 A와 점 B에 대해서 쓸 수도 있습니다. 하지만 식이 3개보다 많아지는 일은 불가능합니다.
즉 이 문제에서 unique하게 풀기 위해 필요한 미지수는 3개라는 뜻입니다. 미지수가 3개보다 적거나 많으면, 해가 없거나 해가 무수히 많기 때문입니다.
따라서 위의 그림은 미지수가 $A_{x},A_{y},B$ 3개가 있고 미지수가 x,y축 운동과 회전 운동 모두 constraints로 작용하고 있어서 평형을 이룰 수 있는 상황이기 때문에 completely constrained rigid body라고 하며, 세 개의 방정식을 통해 각 미지수를 알아낼 수 있기 때문에 statically determinate라고 합니다.
이제 3가지 structure cases를 소개할 텐데 각 문제는 거의 동일해보이지만 약간의 차이가 있습니다.
아래 예시들은 모두 정역학적으로 풀 수 없는 문제들입니다.
이를 Statically indeterminate라고 합니다.

이 경우는 A,B 모두 Pin이 있는 경우이고 x,y축 방향으로 힘이 모두 작용합니다. 또한 방향이 정해지지 않아서 x,y 축 모두 미지수로 작용하게 됩니다. 즉, 주어진 $P,Q,S,W$에 대해서 $A_{x},A_{y},B_{x},B_{y}$는 모두 미지수입니다.
앞서 말했듯이 이 structure에서 나올 수 있는 equation은 3개이므로 미지수와 방정식 개수가 맞지 않습니다.

A,B에 Roller가 있는 경우에는 닿아있는 평면에 수직인 방향으로 힘이 작용해서 미지수가 $A,B$ 두 개밖에 없고 이 문제 역시 방정식이 3개인 것에 비해 미지수 개수가 부족합니다.
또한 이 상황을 partially constrained라고 하는데 vertical motion에 대해서는 제한이 있지만 horizontal motion에 대해서는 제한할 수 있는 방법이 없기 때문입니다. (방정식에 비해 충분한 constraints가 주어지지 않을 때)

이 경우에는 미지수 $A,E,B$ 3개에 방정식도 3개이므로 문제가 없을 것 같지만 문제 조건 상에서는 horizontal motion을 막을 수 있는 조건이 없기 때문에 improperly contrained truss라고 볼 수 있습니다. 따라서 이 문제 역시 statically indeterminate입니다.
4. Reactions for a Three-dimensional Structure


'기계공학 Mechanical engineering > 고체역학 Statics & Solid mechanics' 카테고리의 다른 글
| [고체역학] Statics Ch6 : Analysis of Structures (0) | 2021.04.29 |
|---|---|
| [고체역학] Statics Ch5 : Centroids and Centers of Gravity (0) | 2021.04.27 |
| [고체역학] Statics Ch3 : Rigid Bodies (2) Moment of a Couple (0) | 2021.04.25 |
| [고체역학] Statics Ch3 : Rigid Bodies (1) Equivalent Systems of Forces (0) | 2021.04.25 |
| [고체역학] Statics Ch2 : Statics of Particles (0) | 2021.04.04 |