two force member, multi-force member로 구성된 structure를 분석하는 방법에 대해서 요약하도록 하겠습니다.
이전 chapter들이 모두 external force를 분석하는 것이 중심이었다면 이제는 internal force를 고려해서 물체의 equilibrium을 분석합니다.
internal force을 무시하고 external force로만 free body diagram을 그렸었습니다.
그런데 structure를 구성하는 parts의 equilibrium을 따질 때는 그 parts의 external force가 structure 관점에서는 internal force이기 때문에 이제 internal force를 고려하는 것입니다.

이 그림에서 보면 전체를 분석할 때는 외부 힘을 보지만, 개별 parts를 분석하면 내부 힘도 고려해야 합니다.

또한 engineering structure 분류하면
1) Truss : two-force members*로 구성된 구조
2) Frame : 적어도 한 개 이상의 multi-force member*로 구성된 구조
3) Machine : 힘을 전달하기 위해 움직이는 parts가 포함된 구조
* two-force member : members acted upon by two equal and opposite forces directed along the member
* multi-force member : members acted upon by three or more forces that, in general, are not directed along the member
1. Truss
joints로 연결된 two force member로 구성된 구조를 truss라고 합니다.
항상 two force member로 생각하기 때문에 각 member의 용접되거나 볼트로 연결된 joint는 pinned된 것처럼 생각합니다. 즉, 모멘트 없이 x,y축 force만 고려하며 연결된 부위를 continuous하게 생각하지 않는다는 말입니다.
truss는 일반적으로 two dimensional structure로 생각합니다.
two force member에 작용하는 힘의 종류
- Tension : 잡아당기는 방향의 힘
- Compression : 압축하는 힘

- Simple truss : basic triangular truss에 두 members와 하나의 joint를 추가해서 만든 truss 구조

이 그림처럼 ABC구조에 member BD와 CD를 추가하고 joint D를 추가해서 simple truss를 만들 수 있습니다.
이렇게 만든 simple truss 구조는 joint가 n개, member가 m개일 떄 $m=2n-3$이라는 관계가 성립합니다.
왜냐하면 구조를 늘릴수록 조인트 1개당 멤버 2개가 추가되기 때문에 $m \propto 2n$, 맨 처음 삼각형 구조는 n=3일 때, m=3이기 때문에 다음과 같은 식이 성립하는 것입니다.
- Rigid truss : load가 가해져도 무너지지 않는 truss
기본적으로 삼각형 구조는 load에도 무너지지 않는 구조입니다.
또한 위의 truss bridge 예시들에서 대부분의 bridge가 simple truss이지만 위에서 baltimore는 simple truss가 아닌 rigid truss입니다.
2. Method of Joints
truss에서 힘을 분석하는 방법에는 2가지가 있는데
하나는 Method of Joints이고 다른 하나는 Method of Sections입니다. 여기서는 전자를 먼저 설명합니다.

다음과 같은 truss 구조에는 ABCD 총 4개의 joints가 있습니다.
각 truss의 member들은 two force memeber이며 양 쪽에 작용하는 힘은 크기와 line of action이 동일하되, 방향이 반대인 경우입니다. 이 사실을 알고, 각 joint에 대하여 힘을 표시하여 평형 방정식을 세울 수 있습니다.
위 그림을 모두 분해하면
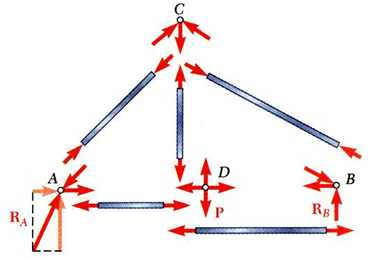
다음과 같습니다. joint A에서는 AC, AD member에 의해 작용하는 힘과 $R_{A}$가 함께 작용하여 평형을 이룹니다.
이렇게 각 joint마다 x,y 축으로 평형 방정식 2개를 얻을 수 있으므로, joint 개수가 n개일 때, 이 truss 구조에서 얻을 수 있는 평형 방정식 수는 2n개입니다.
method of joints는 joint를 이동가면서 각 joint에 대해 방정식을 푸는 방법입니다.
3. Method of Sections

method of sections는 method of joints보다 더 효율적으로 원하는 joint의 힘을 알 수 있는 방법입니다.
위의 그림에서 빨간 점선 n-n으로 구조를 자르면, ABC로 구성된 부분과 DEG로 구성된 부분으로 나뉩니다. 이 각각의 잘린 부분에 대해 평형 방정식을 세울 수 있습니다.

이 그림에서 $F_{BD},F_{BE},F_{CE}$라는 내부 힘을 표시할 수 있습니다. 이 때 힘의 방향은 tension인지, compression인지 알 수 없으므로 임의로 설정한 것입니다. 보통은 문제풀 때 모두 tension으로 잡은 다음에, 힘이 음수가 나오면 compression으로 생각하는 것이 편합니다. 본인이 일관되게 힘의 방향을 설정해주는 것이 중요합니다. (따라서 모든 힘을 compression으로 가정해도 상관은 없습니다.)
이 방법의 장점은 다른 힘에 대한 정보를 모두 가지고 있지 않아도 원하는 내부 힘을 골라서 구할 수 있다는 것입니다.
예를 들어 위의 그림에서 주어진 $P_{1},P_{2}$를 알고 있을 때 $F_{BD}$를 구하고 싶다면, 물론 $F_{BE},F_{CE}$를 구하면 아주 쉽게 $F_{BD}$를 알아낼 수 있기는 하지만, 점E에 대한 $\sum M_{E} =0$ 평형 방정식을 세워서 다른 힘에 대한 고려없이 풀 수도 있습니다. 물론 거리를 구하는 게 조금 귀찮은 부분이긴 하지만 이렇게 Method of sections가 사용될 수 있다는 점을 말하고 싶었습니다.
4. Trusses Made of Several Simple Trusses

만약 simple truss로 이루어진 구조가 있다면 그 구조의 member가 m개, joint가 n개일 때 구조상
$m=2n-3$이라는 것을 앞서서 얘기했습니다.
그리고 method of joints에서 각 joint당 2개의 평형 방정식이 나오고 따라서 2n개의 평형 방정식이 나온다는 것을 알고 있습니다. (전체 strucuture에 대한 평형 방정식을 추가로 세울 수 있겠지만 어차피 joint로 구한 방정식과 관계되어 있으므로 새로운 정보를 얻을 수 없습니다.) 각 member는 two-force member이므로 한 쪽에 작용하는 힘 1개가 미지수가 됩니다. 즉, member에 의해 생기는 미지수는 m개입니다.
방정식 : 2n개
member에 의해 생기는 미지수 : m개
simple truss들로 이루어진 구조에서 추가로 가능한 미지수 : 3개 ($\because m+3=2n$)
따라서 이 구조에서 statically determinate하기 위해 필요한 support reaction은 3개입니다.
$m>2n-3$일 때 overrigid and statically indeterminate
$m<2n-3$일 때 nonrigid
m이 2n-3보다 작으면 nonrigid하지만 만약 support reaction이 충분하면 무너지지는 않습니다.

이 경우에는 m이 2n-3보다 1만큼 작지만 support reaction이 4개이기 때문에 $m+4=2n$이 성립해서 statically determinate하게 된 경우입니다. 다만 support가 없다면 이 구조 자체로는 rigid할 수 없습니다.
또 주의해야할 점은 $m+r=2n$(r은 support reaction의 수)가 성립하면 방정식 개수와 미지수 개수가 동일하기 때문에 statically determinate할 것 같지만 이렇게 support없이는 nonrigid한 구조는 개별 rigid parts에 대해서 free body diagram을 그려서 모든 미지수가 general loading conditions에 대해서 풀리는지 확인해봐야 합니다.
$m+r=2n$은 성립하더라도 만약 member와 support가 잘못된 위치에 있으면 모든 미지수를 다 알아낼 수는 없는 상황이 있을 수 있기 때문입니다.
즉, $m+r=2n$은 statically determinant, rigid, and completerly constrained의 필요조건이지 충분조건은 아닙니다.
5. Analysis of Frames

다음과 같은 상황에서 BE는 Two-force member지만 CF, DA는 multi force member입니다. 이렇게 multi-force member를 포함한 구조는 frame이라고 합니다.

위 상황에 대해서는 다음과 같이 free body diagram을 그릴 수 있고, $T, A_{x}, A_{y}$가 미지수인 외부 힘입니다. 이 미지수들은 평형 방정식을 통해서 알 수 있습니다.
그런데 후에 우리가 배울 내용은 part에 대한 내부 힘인 경우가 많습니다. material이 힘과 모멘트에 대해 어떻게 반응하는지를 알기 위함입니다. 따라서 개별 member들의 힘 분석을 어떻게 하는지도 알아보겠습니다.
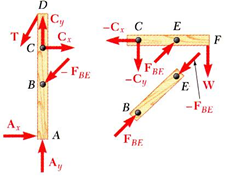
two force member는 힘의 line of action은 알지만 크기를 모르고, two force member가 아닐 때는 joint에서 크기와 방향 모두 고려해줘야하므로 미지수가 x,y축 1개씩 총 2개가 생깁니다. (C 지점과 E 지점을 비교해보세요.)
$T,A_{x},A_{y}$에 대해서 구한 다음에 각 member에 대해 평형 방정식을 세워서 힘을 구할 수도 있고, 개별 member에 대해서 차근차근 풀어도 됩니다.
6. Machine
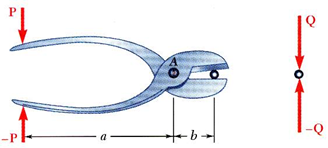
machine 역시 multi-force member를 적어도 한 개 이상 포함하고 있는데, frame과 다른 점은 frame은 load에 대해 정적으로 지탱하는 목적으로 있다면, machine은 힘을 전달하는 목적으로 있다는 것입니다.
위의 machine의 경우 P라는 힘을 줘서 원형의 물체에 Q라는 힘을 전달하기 위해 존재합니다.
따라서 free body diagram을 그리면

'기계공학 Mechanical engineering > 고체역학 Statics & Solid mechanics' 카테고리의 다른 글
| [고체역학] Statics Ch7 : Internal Forces and Moments (2) Cable (0) | 2021.05.06 |
|---|---|
| [고체역학] Statics Ch7 : Internal Forces and Moments (1) Beam (0) | 2021.05.04 |
| [고체역학] Statics Ch5 : Centroids and Centers of Gravity (0) | 2021.04.27 |
| [고체역학] Statics Ch4 : Equilibrium of Rigid Bodies (0) | 2021.04.25 |
| [고체역학] Statics Ch3 : Rigid Bodies (2) Moment of a Couple (0) | 2021.04.25 |