statics 이후에 배울 solid mechanics를 배우기 위해 중요한 단원입니다.
beam과 cable에 load가 작용할 때 그 내부에 어떤 힘이 작용하는지, 즉, internal force를 분석합니다.
이전에도 frame을 다루면서 internal force에 대해서 보기는 했지만 주로 external force를 다뤘었습니다.
주로 beam과 cable structure에 대해서 분석하며, 내부 힘에는 tension/compression(단면에 수직하게 작용하는 힘), shear(단면과 나란한 방향으로 작용하는 힘)이 있고, bending moment를 다룹니다. (물론 자세한 분석은 solid mechanics에서!)
1. Internal Forces in Members
internal force에 대해서 자세히 알아보겠습니다. truss를 공부했으면 이해하기 쉬울 것입니다.

AB two force member가 있을 때 중간에 C지점에서 관찰할 때 AC와 CB는 평형을 이루어야 합니다. 따라서 C지점에서는 각각 -F, F force가 작용하게 됩니다.
마찬가지로 아래 두 개의 구조에서도 중간에 잘라서 보았을 때 각 지점에서는 작용반작용에 의해, 같은 크기, 반대 방향의 힘과 모멘트를 받게 되고 잘려진 각 부분은 평형을 만족해야 합니다.
2. Various Types of Loading and Support

beam에서 작용하는 load에는 두 종류가 있는데 하나는 왼쪽 그림의 (a)와 같이 특정 지점에 집중적으로 작용하는 concentrated load가 있고 다른 하나는 distributed load입니다. 물론 두 종류의 힘이 동시에 작용하는 경우도 있습니다.
beam을 설계할 때는 빔의 internal force로 작용하는 shear force와 bending moment를 구하고, 그 force와 moment를 견딜 수 있는 형상을 찾습니다.
또 우리가 앞서 본 analysis of structures에 statically determinate한지 아닌지에 대한 내용이 포함되어 있었습니다.
beam 역시 structure이기 때문에 support에 따라서 해결할 수 있는지 아닌지가 결정됩니다.
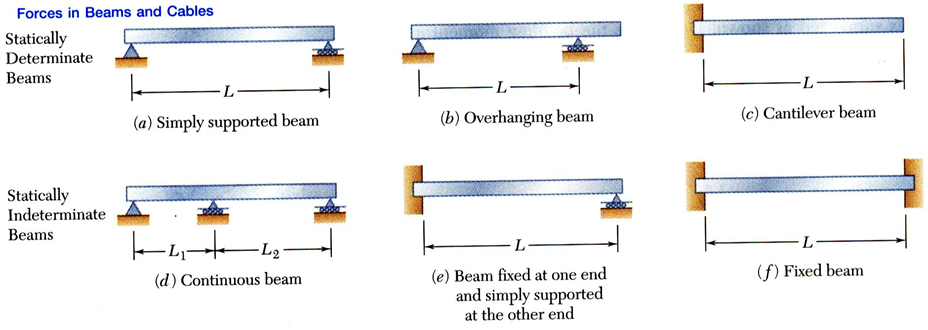
$F_{x},F_{y},M$ 각각 평형방정식을 세우면 3개의 equation이 나오므로 support reaction이 3개여야 statically determinate합니다.
3. Shear and Bending Moment in a Beam
빔에 concentrated load나 distributed load가 작용할 때 빔의 위치에 따른 내부 힘을 그래프로 나타낼 수 있습니다.


예를 들면 다음과 같은 상황에서 C점에서의 bending moment(M)와 shear(V)를 나타낼 수 있는데 이는 각 지점마다 빔의 단면에 평행한 힘과 빔이 굽어지게 만드는 모멘트가 작용하고 있다는 뜻입니다.
또한 Positive sense의 bending moment와 shear는 위의 그림과 같이 왼쪽 빔 기준으로 shear는 아래 방향, moment는 지면으로 나오는 방향입니다.
Shear and Bending moment diagrams
shear-bending moment diagram을 그리는 방법도 알아야 합니다.

다음과 같은 상황(concentrated load 하나만 작용하는 상황)에서

support reaction를 구할 수 있습니다. (support reaction은 3개)

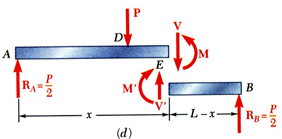
이제 shear와 bending moment를 구하기 위해서는 각각의 지점에서 shear와 bending moment를 그려야합니다.
위의 상황처럼 concentrated load만 작용할 때는 A와 D 지점 사이 모두에서 shear force가 동일하고, bending moment는 거리에 비례합니다.
또한 D와 B 지점 사이의 shear force와 bending moment 역시 이 사이에서는 shear force가 동일하게 bending moment는 거리와 관계가 있습니다. 문제를 간단하게 풀기 위해서는 $V, V^{'}$이 동일한 크기에 반대 방향이고 $M, M^{'}$ 역시 같은 크기, 다른 방향이므로 이 점을 이용해서 더 간단하게 구할 수 있는 값을 구하면 됩니다.
예를 들면 위 그림(c)에서 AC에 대해서 shear force와 bending moment를 구하기 쉽고 상대적으로 CB에 대해서 구하는 게 어려우므로 AC에 대해서 구하고, 그림(d)에서 AE에 대해서 구하기 보다는 EB에 대해서 구하는 게 상대적으로 편하므로 EB에 대한 평형 방정식으로 shear, bending moment를 구합니다.
그 결과
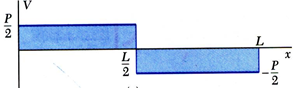

4. Relations Among Load, Shear, and Bending Moment
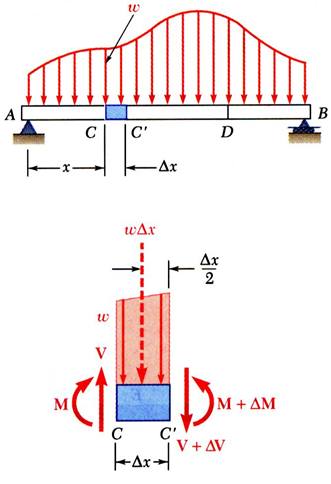
load와 shear, bending moment 간에는 관계가 있습니다. 그리고 이 관계를 알면 훨씬 수월하게 shear, bending moment diagram을 그릴 수 있습니다.
beam의 미소부분($\Delta x$)에 대해 힘과 모멘트 평형 방정식을 세운 다음에
$\Delta x \rightarrow 0$으로 보내면 아래와 같은 식을 유도할 수 있습니다.
$\frac{dV}{dx}=-w$
shear force를 미분하면 beam에 작용하는 load가 나옵니다.
$\frac{dM}{dx}=V$
Bending moment를 미분하면 beam에 작용하는 shear force가 나옵니다.
따라서 이렇게 미분, 적분 관계를 알고 있으므로
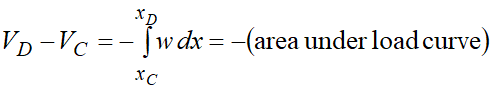

내가 원하는 구간에 작용하는 shear force와 bending moment를 다음 식을 통해서 알 수 있습니다. (물론 역으로 미분해서도 구할 수 있음)
주의해야 할 점은 이 상황은 distributed load이고, concentrated load의 경우에는 concentrated load가 작용하는 지점에서 shear force는 미분 불가능하므로(위의 shear-bending moment diagram 파트 참고) load에 대해서 위 공식처럼 생각하는 것은 다소 까다롭고, shear force를 적분해서 bending moment를 구하거나 bending moment를 미분해서 shear force를 구하는 것은 가능합니다.

distributed load에 대해서 shear force와 bending moment diagram을 그리면 아래와 같은 그래프가 나옵니다. moment를 미분했을 때 $x=\frac{L}{2}$에서 0이고 shear force에서도 $x=\frac{L}{2}$일 때 0의 값을 가집니다.
또한 Shear force는 선형 방정식인데 이를 적분하면 이차방정식인 bending moment를 구할 수 있습니다.


다음에는 cable의 internal force에 대해서 다루겠습니다.
'기계공학 Mechanical engineering > 고체역학 Statics & Solid mechanics' 카테고리의 다른 글
| [개념] Equivalent와 Equipollent force (0) | 2021.05.16 |
|---|---|
| [고체역학] Statics Ch7 : Internal Forces and Moments (2) Cable (0) | 2021.05.06 |
| [고체역학] Statics Ch6 : Analysis of Structures (0) | 2021.04.29 |
| [고체역학] Statics Ch5 : Centroids and Centers of Gravity (0) | 2021.04.27 |
| [고체역학] Statics Ch4 : Equilibrium of Rigid Bodies (0) | 2021.04.25 |