cable 역시 beam 처럼 internal force를 고려하는 물체이지만, beam과 다르게 cable은 x축에 따른 y축의 위치가 달라서 이 부분을 고려해야 합니다.
1. Cable With Concentrated Loads
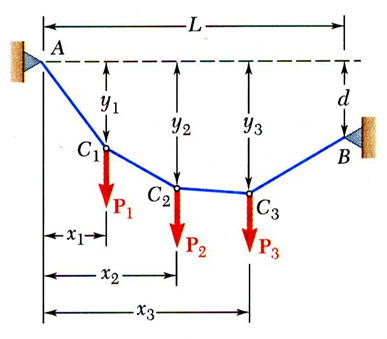
다음과 같이 일부 지점에만 집중적으로 load가 작용할 때 몇 가지 가정이 필요합니다.
load가 vertical하게 작용하고 있고, cable의 무게는 무시하며, cable은 flexible하므로 bending에 대해 고려하지 않습니다. 또 힘이 작용하는 cable의 각 부분은 two force member처럼 취급합니다.
cable 분석은 최종적으로 cable이 어떤 모양을 갖는지, 즉 주어진 load에 대해 cable의 vertical distance가 어떤지 구합니다.
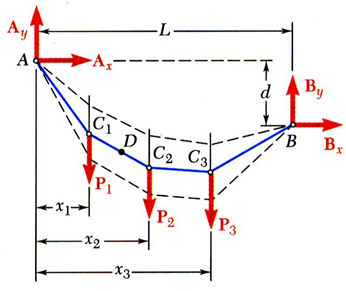
지금 A,B는 reaction force가 작용하므로, 둘 다 pin이니 x,y축 힘 모두 작용합니다. 3개의 equations과 4개의 unknowns를 구하기에는 equations 수가 부족하므로 internal force를 고려하도록 합니다.
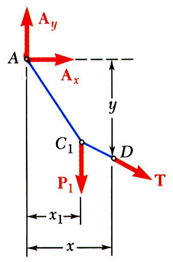
따라서 다른 지점에 대해 평형 방정식을 추가로 구해서 문제를 풀어야 합니다. 그래서 만약 특정 지점에 대한 정보가 미리 주어져있다면 그 지점에 대해서 평형 방정식을 세워서 문제를 풉니다.
만약 왼쪽 그림처럼 D지점에 대한 정보가 이미 주어져있어서 $\sum M_{D}=0$이라는 방정식을 이용해서 방정식 하나를 추가할 수 있습니다.
이렇게 하면 $A_{x},A_{y}$를 구할 수 있으므로 다른 지점의 vertical distance를 구할 수 있습니다.

다른 지점의 vertical distance를 구하기 위해 $\SUM M_{C_{2}}=0$ 방정식을 세워서 $y_{2}$를 구하면 됩니다.
또 흥미로운 사실은 $\sum F_{x}=0, \sum F_{y}=0$평형 방정식을 세웠을 때
$T_{x},T_{y}$를 구할 수 있는데, $A_{x}$는 고정된 값이고, $P_{1},P_{2}$는 vertical하게 작용하므로 $T_{x}$는 항상 $A_{x}$값으로 일정하다는 점입니다.
또한 cable을 two force member로 생각하고 있어서 왼쪽 그림의 $\theta$는 $C_{2},C_{3}$가 이루는 각이라고 봐도 될 것입니다.
2. Cables with Distributed Loads
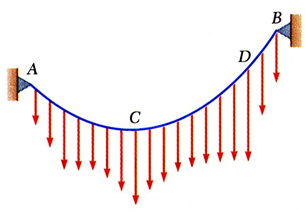
다음과 같이 cable에 load가 distributed되어있는 경우 그 vertical distance가 연속적으로 변하게 됩니다. 이 vertical distance를 구하기 위해 몇 가지 가정을 하면,
cable은 curve 모양을 가지며 늘어져있고, internal force는 curve의 tangent를 따라서 tension force를 가진다고 생각합니다.
또한 위의 concentrated force와 달리 여기서는 cable의 무게도 고려합니다.

위 그림에서 CD지점을 잘라서 free body diagram을 그린 것입니다.
여기서 C는 cable에서 가장 낮은 지점을 위미하고 이 낮은 점을 중심으로 양 쪽으로 넓혀가면서 free body diagram을 그릴 수 있습니다. cable이 가장 낮은 지점에서는 horizontal force만이 작용하므로
$T\cos \theta = T_{0}$
$T\sin \theta = W$
$T = \sqrt{T_{0}^{2}+W^{2}}$
다음 식이 성립합니다. 즉, T의 horizontal component는 항상 일정하고, T의 vertical component만 C에서 어느 지점까지를 free body diagram으로 잡았는지에 따라서 결정나게 됩니다.
즉, 가장 낮은 지점에서 tension은 최소가 되고, 가장 낮은 지점으로 가장 먼 지점까지의 tension은 최대가 됩니다.
3. Parobolic Cable



이 경우는 수평으로 weight가 균일하게 분포되어 있을 때입니다. 즉, 가장 낮은 지점에서 양 쪽으로 확장할 수록 그 수평 길이만큼 무게가 증가한다고 보면 됩니다.
$\sum M_{D}=0 : wx \frac{x}{2}-T_{0}y=0$
$y = \frac{wx^{2}}{2T_{0}}$
즉, y는 x에 대한 parabolic한 형태로 나타납니다. (그래서 parabolic cable)
4. Catenary cables
cable 무게가 균일하게 분포해있는 경우를 catenary cable case로 생각하고 분석합니다. 자신의 무게로만 hanging되어 있을 때 그 형상이 포물선보다는 쌍곡함수로 나타납니다.


앞서 본 parabolic cable과 다르게 catenary cable은 길이(s)당 균일한 무게가 분포되어있다고 생각합니다. 즉, cable의 vertical distance를 고려해서 각 x지점에 load가 달라진다는 뜻입니다.

길이를 $s$, 길이당 weight를 $w$라고 할 때 이제 무게는 $ws$라고 표현하고 위 그림과 같이 T를 표현합니다.
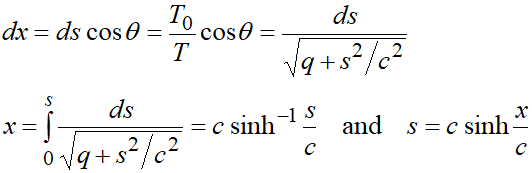
위에서 cable이 parabolic curve인 것과 달리 여기서는 cable의 shape가 쌍곡 함수로 나타납니다.
'기계공학 Mechanical engineering > 고체역학 Statics & Solid mechanics' 카테고리의 다른 글
| [개념] Equivalent와 Equipollent force (0) | 2021.05.16 |
|---|---|
| [고체역학] Statics Ch7 : Internal Forces and Moments (1) Beam (0) | 2021.05.04 |
| [고체역학] Statics Ch6 : Analysis of Structures (0) | 2021.04.29 |
| [고체역학] Statics Ch5 : Centroids and Centers of Gravity (0) | 2021.04.27 |
| [고체역학] Statics Ch4 : Equilibrium of Rigid Bodies (0) | 2021.04.25 |