지금까지 배웠던 controllability와 observability를 실제 예시를 통해 보기로 하겠습니다. (이전 글 참고)
이번에는 그림도 들어가고 matrix의 차원도 높아서 그림 위주로 작성하려고 합니다.
1. Controllability

위와 같은 dynamic system에서 $x_{1}$은 $m_{1}$의 position, $x_{2}$는 velocity로 설정했습니다.
마찬가지로 $m_{2}$의 position, velocity 각각 $x_{3},x_{4}$로 설정했습니다.
따라서 state는 $\begin{bmatrix}x_{1}\\x_{2}\\x_{3}\\x_{4}\end{bmatrix}$

그림에서 위 식이 이 system의 equation이고
아래 P matrix는 controllability matrix입니다.
P matrix의 determinant를 통해 rank를 알아보겠습니다.
저의 경우에는 P matrix가 문자로 된 식이므로 matlab에서 determinant를 구하는 기능을 사용했습니다.
(참고 : normal-engineer.tistory.com/77)

$\frac{m_{1}}{k_{1}}\neq \frac{m_{2}}{k_{2}}$이어야 이 시스템은 controllable합니다.
2. Observability
마찬가지로 동일한 시스템에 대해서 observability를 살펴보겠습니다.

만약 $x_{1}+x_{3}$을 관찰할 수 있을 때(두 mass 사이의 거리를 측정)
Q matrix를 구한 다음에 determinant를 알아보았습니다.
$\frac{m_{1}}{k_{1}}\neq \frac{m_{2}}{k_{2}}$이면 Q가 full rank이므로 observable합니다.
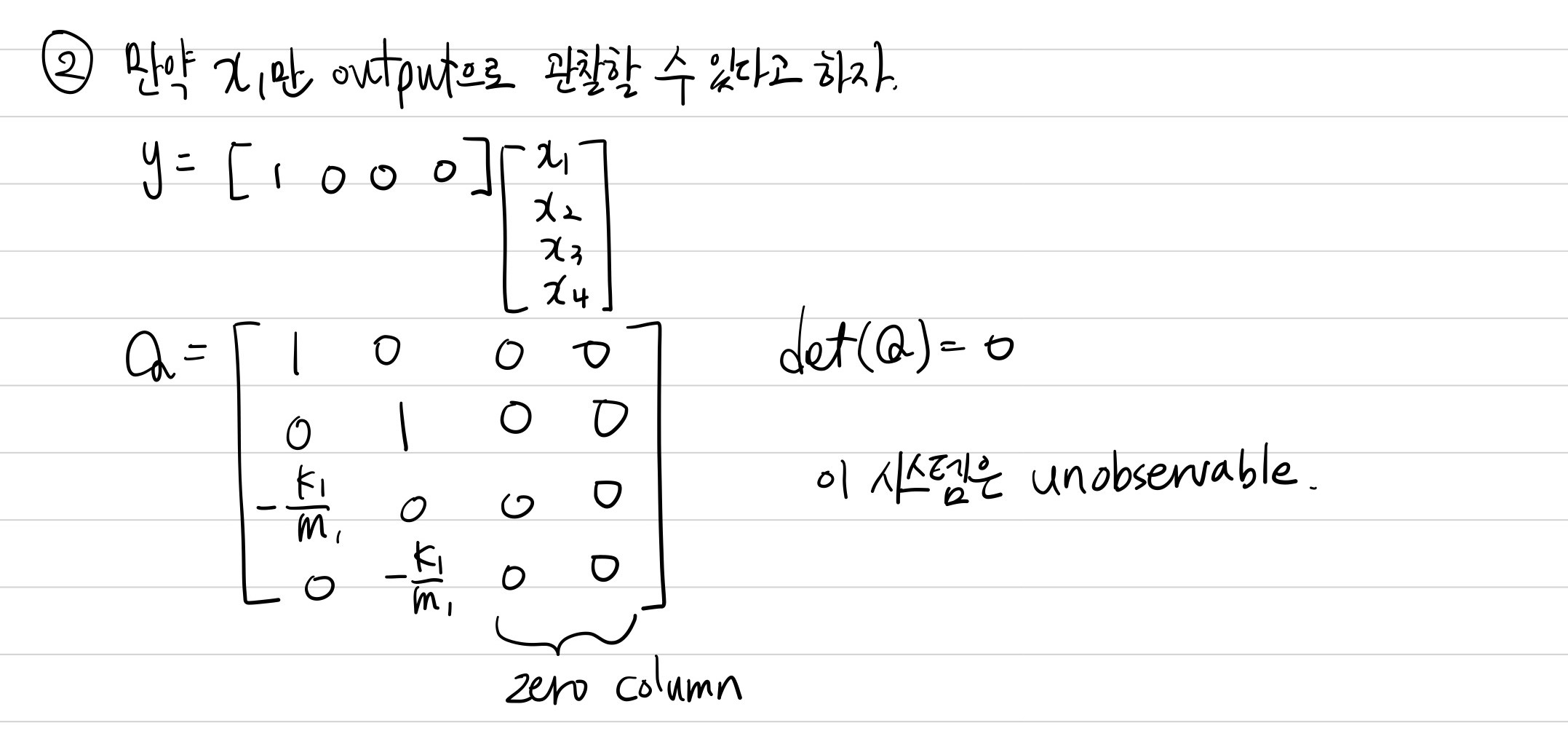
만약 센서가 $m_{1}$에만 달려서 position을 관찰할 수 있다고 하겠습니다. 그러면 $x_{1}$만 관찰할 수 있으므로 $C=\begin{bmatrix}1&0&0&0\end{bmatrix}$가 되므로 이를 이용해 Q matrix를 구할 수 있습니다.
zero column이 존재하기 때문에 $k_{1},m_{1}$에 관계없이 Q matrix는 full rank가 아니므로, 이 시스템은 unobservable합니다.

마지막으로 $x_{1}$과 $x_{3}$를 독립적으로 관찰할 수 있을 때 Q matrix를 구했다. $nr \times n$ matrix이기 때문에 $8 \times 4$ matrix입니다. 위의 matrix를 보면 알 수 있는 것처럼 column에서 $k_{1},k_{2},m_{1},m_{2}$ 값과 관계없이 항상 rank 4이므로 full rank로 observable합니다.
아래는 MATLAB에서 P, Q matrix에 대해 determinant를 구할 수 있는 code입니다.
% controllability & observability matrix
k1 = sym('k1');
k2 = sym('k2');
m1 = sym('m1');
m2 = sym('m2');
P = [1 1/m1 0 -k1/(m1^2); 1/m1 0 -k1/(m1^2) 0; 0 1/m2 0 -k2/(m2^2); 1/m2 0 -k2/(m2^2) 0];
det_P = det(P);
A = [0 1 0 0; -k1/m1 0 0 0; 0 0 0 1; 0 0 -k2/m2 0];
C = [1 0 0 0; 0 0 1 0];
Q = [C;C*A;C*A^2;C*A^3];
det_Q = det(Q);
'연구 Research > 제어 Control' 카테고리의 다른 글
| [제어] Control theory 관련 레퍼런스 정리 (1) | 2021.11.11 |
|---|---|
| [고등자동제어] Singular Value Decomposition과 Degree of Controllability (0) | 2021.02.26 |
| [고등자동제어] Observability in Continuous time (0) | 2021.02.25 |
| [고등자동제어] Controllability in Continuous time (0) | 2021.02.25 |
| [고등자동제어] Observability in discrete time (0) | 2021.02.23 |