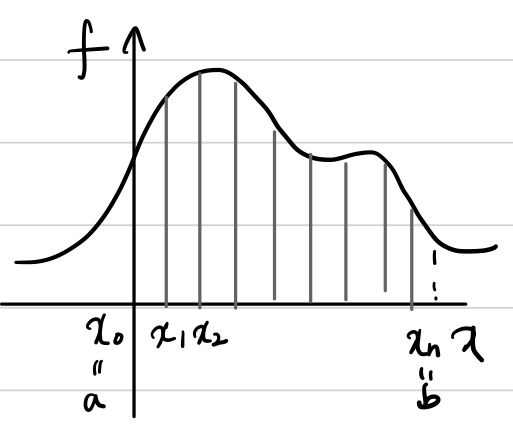
이번에는 수치해석 적분 중 하나인 Simpson's rule에 대해서 공부하겠습니다. (mid point rule과 trapezoidal rule에 대해서는 이전 글을 참고해주세요.) 1. Simpson's rule $\text{Rectangular (mid point) rule error : }R(f)=\frac{1}{24}h_{i}^{3}f^{''}(y_{i})+\theta (h_{i}^{5})$ $\text{Trapezoidal rule error : }T(f)=-\frac{1}{12}h_{i}^{3}f^{''}(y_{i})+\theta (h_{i}^{5})$ $y_{i}=\frac{x_{i}+x_{i+1}}{2}\text{ : mid point}$ $h_{i}=x_{i+1}-x_{i}$ 위의 두 ..

수치해석 수업을 들으면서 수치해석으로 문제를 푸는 과정을 거치고 있습니다. (수치해석 정리글은 나중에 한꺼번에 올라갈 예정) 수치적으로 interpolation을 하는 것 중에 사용되지는 않지만 구현하기는 쉬운 Lagrangian polynomial에 대해 구현한 것을 공유하고자 합니다. Lagranian polynomial을 만드는 방법에 대한 설명은 normal-engineer.tistory.com/95 [수치해석] Interpolation (1) - Polynomial interpolation 이번에는 수치해석에서 사용하는 interpolation 방법에 대해서 알아봅니다. 우리의 목적은 주어진 discrete data $(x_{i},y_{i})\text{ for }i=1,2,3,\ldots, n$..

interpolation, differentiation에 이어서 integration을 수치해석적으로 수행해보겠습니다. 1. Introduction $x_{0}(=a)$부터 $x_{n}(=b)$까지 적분을 하려고 합니다. 우리는 discrete하게밖에 계산할 수 없으므로, $I=\int_{a}^{b}f(x)dx=\sum_{j=0}^{n}f_{j}\cdot \omega_{j}$ 적분을 오른쪽 식처럼 계산해야합니다. 이 때 $\omega_{j}$는 weighting factor라고 부릅니다. 이 전에 Lagrange polynomial을 배웠고, 그 polynomial 식은 $p(x)=\sum_{j=0}^{n}f_{j}L_{j}(x)$입니다. 이 방법을 통해 내가 알고 있는 데이터 점들을 충족하는 함수 식을..

1. Order of accuracy / Leading order of error 지금까지 numerical method를 이용해 interpolation하거나 미분을 할 때 어떻게 구하는지, 또 그렇게 했을 때 error가 어떻게 되는지 알아봤습니다. Order of accuracy, Leading order of error는 수치해석에서 가장 신경쓰는 요소 중 하나입니다. error의 order는 클수록 '대체로' 좋습니다. $\theta (h^{p}) \rightarrow p \log \theta(h)$ p는 곧 $\log E$와 $\log (h)$의 기울기이기 때문에 p가 클수록 에러가 작아지면 더 급격하게 에러가 작아집니다. 만약 numerical method를 이용해 derivative를 구하..

1. General procedure to obtain first difference derivatives 이전에 한 논의에 이어서, taylor table을 만드는 과정에 대해서 알아보고자 합니다. 일단 한 예시를 보고 그것을 확장할 수 있습니다. ex) $f_{j}^{'}$를 $f_{j},f_{j+1},f_{j+2}$를 이용해 구하고자 합니다. 최종적으로 $f_{j}^{'}+a_{0}f_{j}+a_{1}f_{j+1}+a_{2}f_{j+2}=\theta(h^{p})\text{, where }h=\Delta x=x_{j+1}-x_{j}=x_{j+2}-x_{j+1}$ 의 형태로 나타냄으로써 $f_{j}^{'}$를 $f_{j},f_{j+1},f_{j+2}$에 대해서 표현하고, 그 때 발생하는 오차의 maxi..

컴퓨터 상에서 미분을 수행하기 위해서는 어떻게 할까? 앞에서 interpolation을 이용해서 식을 구한 다음에 미분을 수행할 수도 있지만, interpolation을 배제하고 each discrete point에서 derivatives를 구해야한다고 생각해보자. # Notation 참고 $x_{B}^{A}$ : $A$는 시간에서의 위치(Timesteps), $B$는 공간에서의 위치를 의미합니다. Taylor series expansion을 통해서 미분값을 구할 수 있는데, 이 때는 미분가능성이 전제로 되어있어야 합니다. $f^{'}(x)=\underset{\Delta x \rightarrow 0}{\lim}\frac{f(x_{i}+\Delta x)-f(x_{i})}{\Delta x}=\underset..

이전 interpolation에서 이어지는 내용입니다. 1. Linear interpolation 일반적으로 smooth한 것이 필요한 게 아니라면 linear interpolation을 사용해도 괜찮을 수 있습니다. 하지만 $f^{'},f^{''}, \text{ or }\int f dx$을 알고 싶은 것이 목적이기 때문에 여기서 linear interpolation은 넘어가겠습니다. 2. Cubic Spline interpolation Spline interpolation은 공학적으로 유용한 interpolation이라고 합니다. 2차 미분도 가능하면서, computational cost도 적기 때문입니다. 예를 들어 bending 문제를 살펴보겠습니다. 외부 힘이 중력만 작용하는 경우 이 시스템을 $..

이번에는 수치해석에서 사용하는 interpolation 방법에 대해서 알아봅니다. 우리의 목적은 주어진 discrete data $(x_{i},y_{i})\text{ for }i=1,2,3,\ldots, n$가 있을 때 두 데이터 points 사이에 있는 point의 value y를 구하고 싶은 것입니다. 또한 우리는 $f^{'},f^{''}, \text{ or }\int f dx$도 알고 싶습니다. (위에서 $f^{''}$까지 요구하는 이유는, 보통 기계공학에서 일반적인 DE는 order가 2nd order DE이므로, 두 번 미분한 값까지 아는 것이 좋기 때문입니다.) 주어진 데이터 안에서 알지 못하는 x에 대한 y값을 알 수 있는 방법은, 주어진 데이터를 가지고 시스템의 함수식을 예측해보는 방법이 ..

normal-engineer.tistory.com/83 이 글과 이어지는 내용입니다. 1. Solution 계산에 필요한 operation cost 앞에서 modeling - transform to multiple ODE - transform to algebraic equation 까지 진행한 다음에는 역행렬을 계산해야합니다. 이 글에서는 matrix의 형태에 따라 역행렬을 구하는 operation cost가 달라진다는 것을 보이려고 합니다. 참고 $\sum_{k=1}^{n}1=n$ $\sum_{k=1}^{n}k=\frac{n(n+1)}{2}$ $\sum_{k=1}^{n}k^{2}=\frac{n(n+1)(2n+1)}{6}$ $\sum_{k=1}^{n}k^{3}=\left ( \frac{n(n+1)}{2}..

이번에는 수치해석 과정을 열전달 예시를 통해서 볼 수 있습니다. 열전달 방정식은 이미 solution이 잘 나와있지만 이 예시를 통해서 수치해석을 하는 과정에 대한 이해를 높일 수 있습니다. 벽에 붙어있는 전도체가 있을 때, 두께는 길이에 비해 매우 작다고 가정하기 때문에 1-Dimensional heat transfer 문제입니다. 수치해석은 크게 세 단계로 나눌 수 있습니다. modeling - transform to algebraic equation - solve algebraic equation 이 문제도 같은 과정을 거치도록 하겠습니다. 1) modeling 위의 시스템을 differential equation(DE)로 만드는 과정입니다. 이 시스템에서 알아내고자 하는 것(solution)은 x..